树型结构是一种重要的非线性数据结构。树型结构在客观世界广泛存在，如组织关系可用树来表示。树在计算机领域也有广泛应用，如在编译程序时，可用树来表示源程序的语法结构(语法树)。又如在数据库系统中，使用树型结构存储索引等信息。森林则是零到多棵树的集合。对森林的研究，都是转化为对树的研究。

树的定义

树(Tree)是n(n≥0)个结点的有限集合。在任意一棵非空树中，有以下两个性质：
(1) 有且仅有一个特定的结点，称为根(Root)。
(2) 当n＞1时，其余的结点可分为m个互不相交的集合T1，T2，…，Tm，其中每一个集合都是一棵树，并且称为根的子树(Subtree)。
这里以一个具有13个结点的树为例，对树型结构进行简单说明。
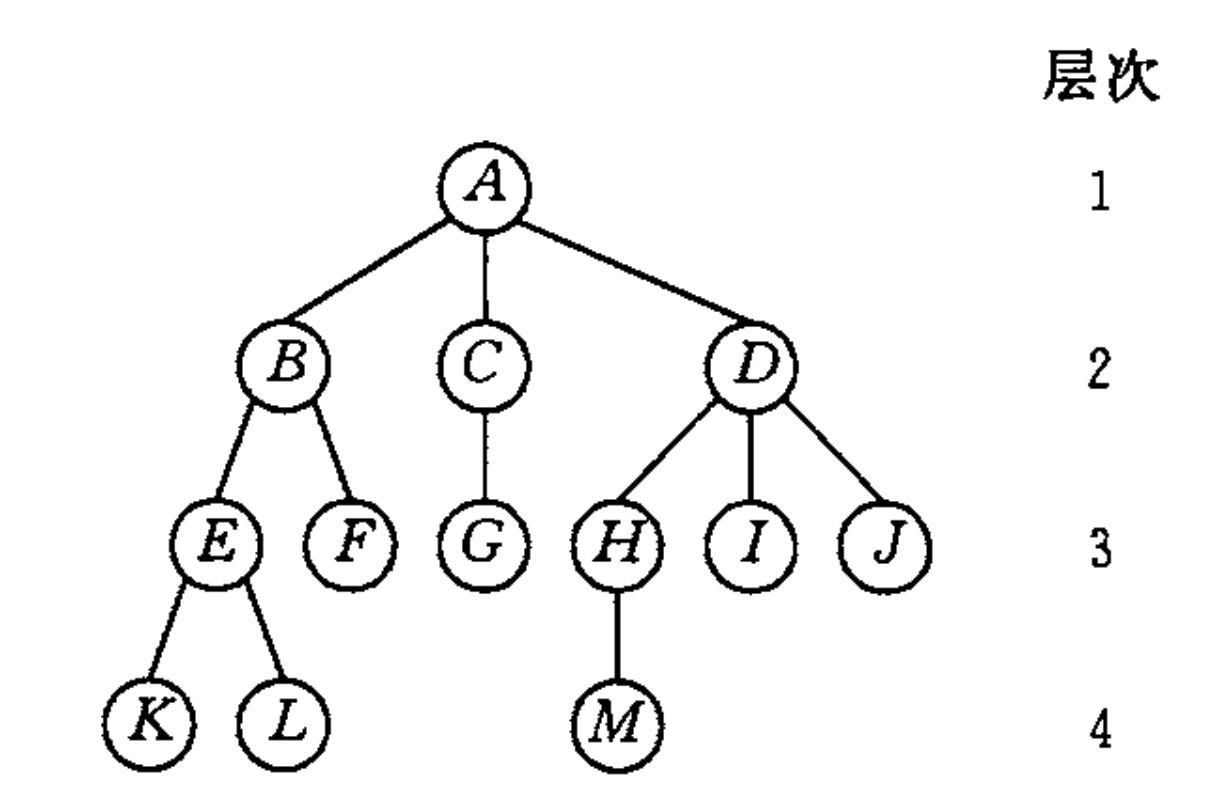
树型结构实例

对上图的树来说，A是根结点，其余三个集合 $T_1=\{B,E,F,K,L\}$ ， $T_2=\{C,G\}$ ， $T_3=\{D,H,I,J,M\}$ 都是子树，且本身也是一棵树，其他子树可类推。
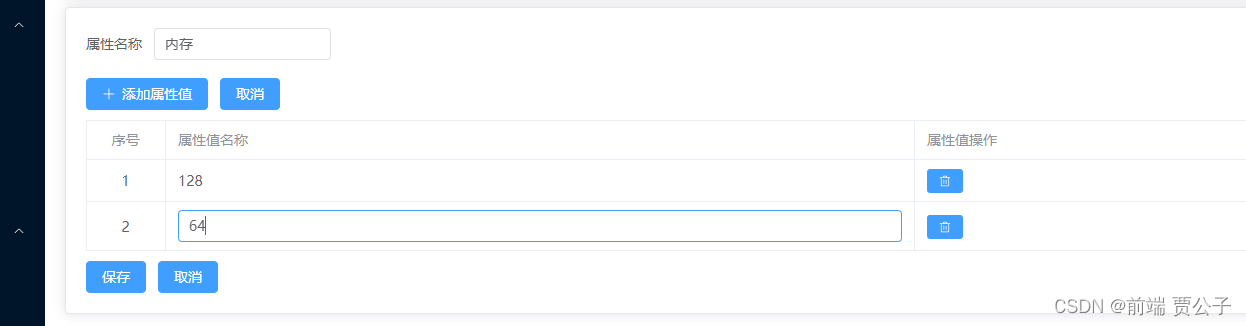
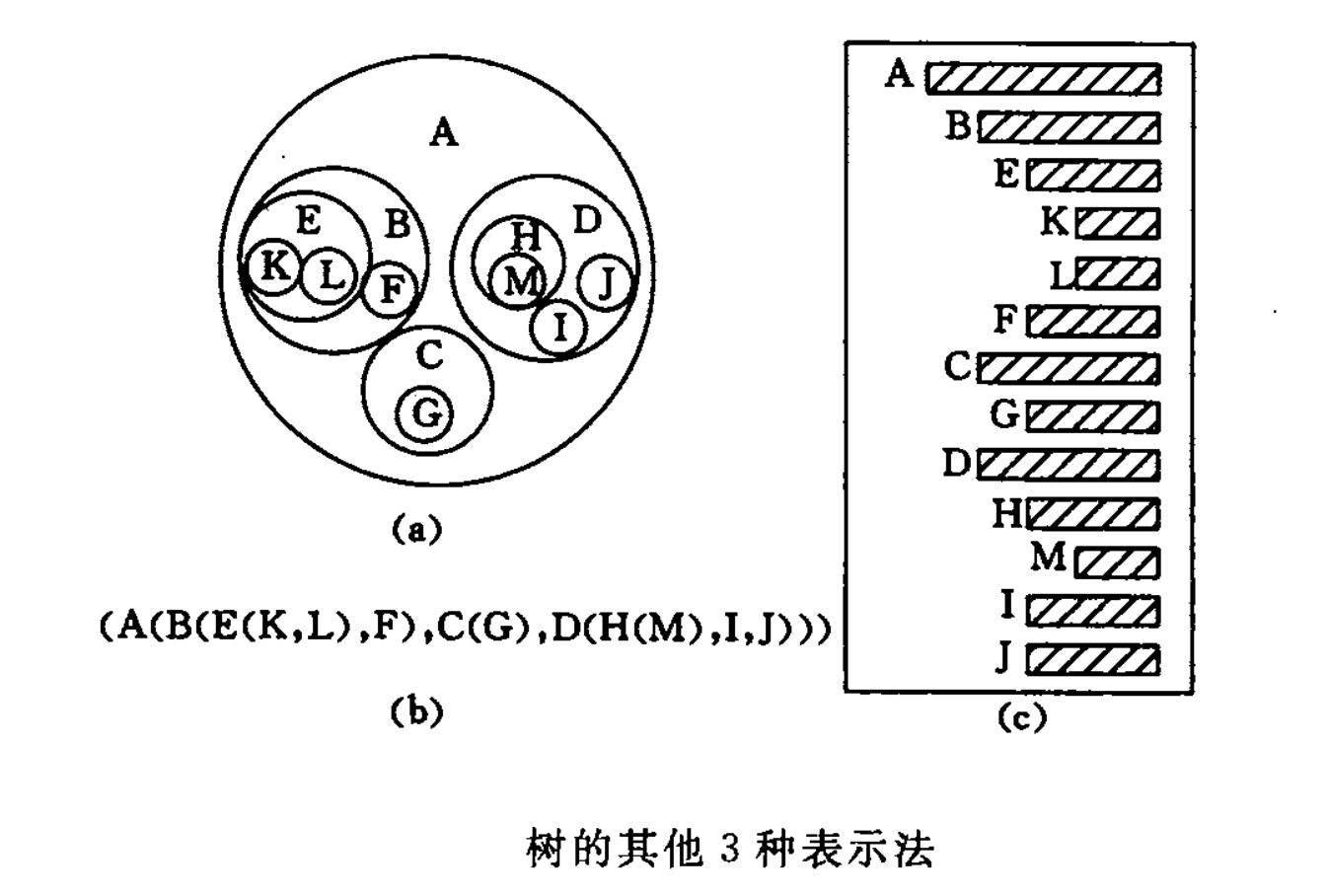
树的结构定义是一个递归的定义，即在树的定义中又用到树的概念，它道出了树的固有特性。需要说明的是，表示树型结构关系，除了使用树型结构，还有其他结构。如嵌套集合、广义表、凹入表示法等。只是，使用树型结构可以更加直观的刻画树。其他表示方法示例见下图：
树的其他表示方法

树的基本术语

接下来介绍树的一些基本术语，统一描述。
树结点(Tree Node)：树中元素的基本单位。包含一个数据元素及若干指向其子树的分支，如上图中的A、B等。而树中唯一没有前驱的结点称为根结点(Root)，如上图的A结点。
结点的度(Degree)：结点拥有的子树个数。如上图中结点A的度为3，结点L的度为0。而度为0的结点称为叶子结点(Leaf)或终端结点。如上图中，K、L都是叶结点。度不为0的结点称为中间结点或分支结点或非终端结点。
树的度(Tree Degree)：树中各结点的度的最大值。如上图中树的度为3。
双亲(Parent)和孩子(Child)：把一个树结点的直接前驱(只有一个)称为该结点的双亲；相反的，把一个树结点的所有直接后继(零到多个)称为该结点的孩子。如上图中，结点B是结点A的孩子，结点A是结点B的双亲。兄弟(Sibling)：同一双亲的孩子之间称为兄弟。如上图中，结点B、C、D互为兄弟。将这些关系进一步推广，结点的祖先(Ancenstor)就是从根到该结点的所经分支上的所有结点，如上图M的祖先为A、D和H。以某结点为根的子树中的任一结点都称为该结点的子孙(Descendant)，如上图B的子孙是E、K、L和F。
树的层次(Level)：从根结点算起，根为第一层，根的孩子为第二层，树中任一结点的层次等于它的双亲的层次加1。树中各结点层次的最大值称为**树的深度(Depth)**或高度。例如，上图中的树的深度为4。
有序树(Ordered Tree)和无序树((Unordered Tree))：如果树中结点的各子树可看成从左至右是有次序的(即不能互换)，则称该树为有序树，否则称为无序树。在有序树中，最左边子树的根称为第一孩子，最右边子树的根称为最后一个孩子。