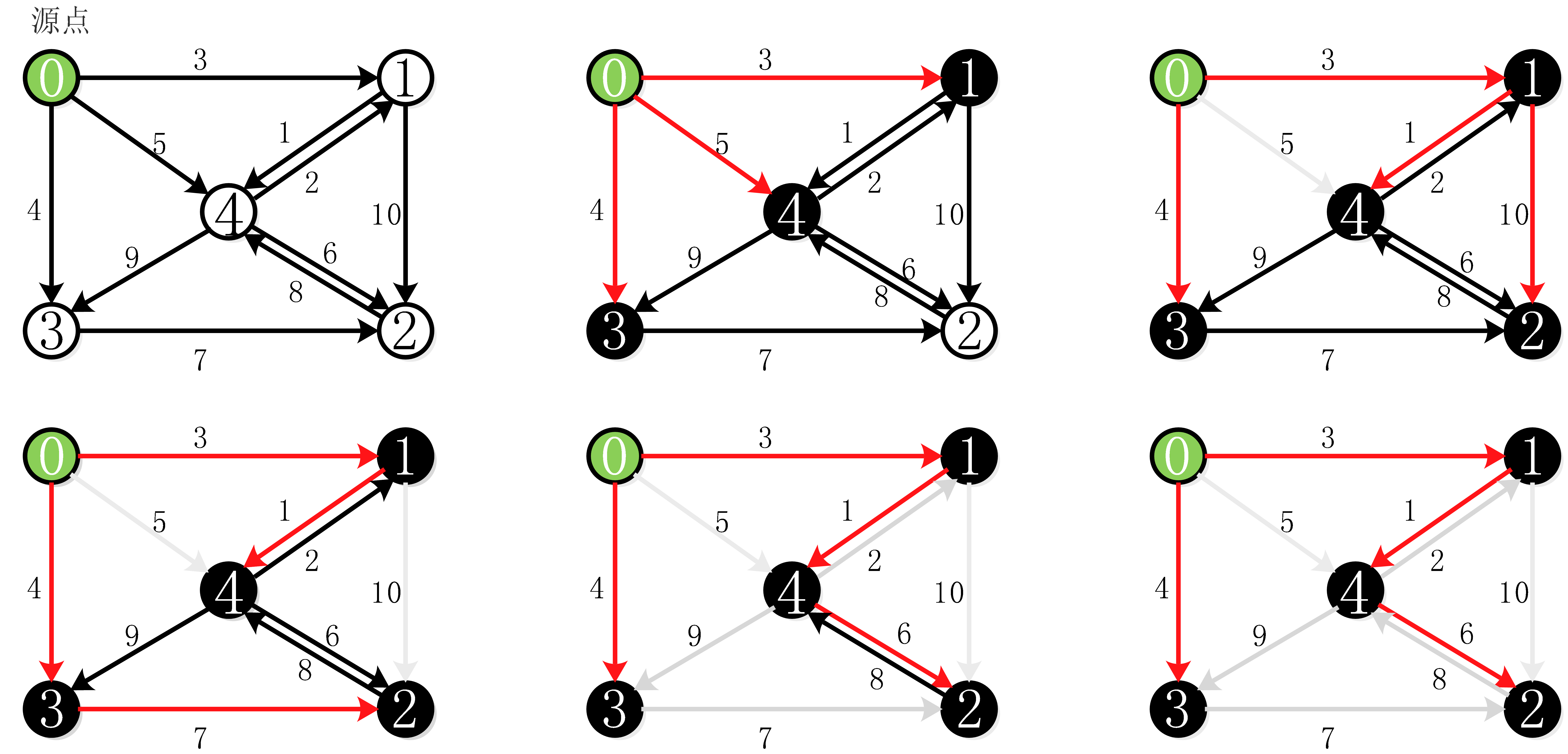
1 主要思想

1.1 数据

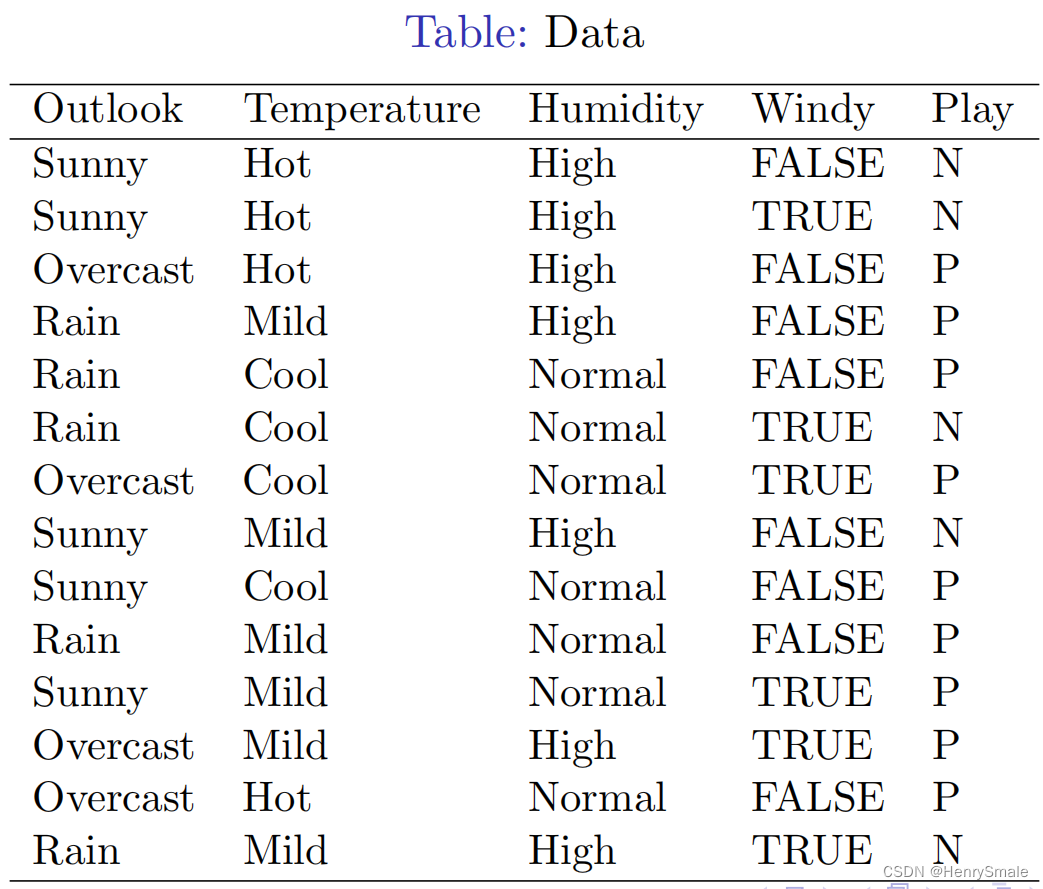
在这里插入图片描述

1.2 训练和使用模型

训练：建立模型（树）
测试：使用模型（树）
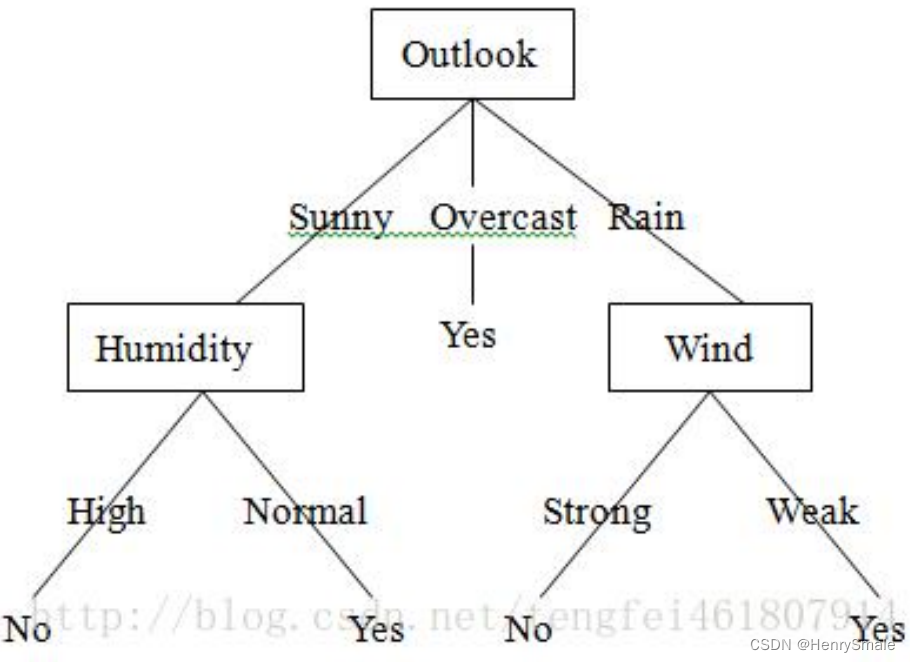
在这里插入图片描述
Weka演示ID3（终端用户模式）

双击weka.jar
选择Explorer
载入weather.arff
选择trees–>ID3
构建树，观察结果

建立决策树流程

Step 1. 选择一个属性
Step 2. 将数据集分成若干子集
Step 3.1 对于决策属性值唯一的子集, 构建叶结点
Step 3.2 对于决策属性值不唯一的子集, 递归调用本函数

演示: 利用txt文件, 按照决策树的属性划分数据集

2 信息熵

问题: 使用哪个属性进行数据的划分?
随机变量 $Y$ 的信息熵为 ( $Y$ 为决策变量)：
$E[I(y_i)] = \sum_{i=1}^n p(y_i)\log \frac{1}{p(y_i)} = - \sum_{i=1}^n p(y_i)\log p(y_i),$
其中 $\log 0 = 0$ .
随机变量 $Y$ 关于 $X$ 的条件信息熵为( $X$ 为条件变量)：
$H(Y∣X)=∑i=1mp(xi)H(Y∣X=xi)=−∑i,jp(xi,yj)log⁡p(yj∣xi).\begin{array}{ll} H(Y | X) & = \sum_{i=1}^m p(x_i) H(Y | X = x_i)\\ & = - \sum_{i, j} p(x_i, y_j) \log p(y_j | x_i). \end{array}$
$X$ 为 $Y$ 带来的信息增益: $H (Y) - H (Y ∣ X)$ .

3 程序分析

版本1. 使用sklearn (调包侠)
这里使用了数据集是数值型。

import numpy as np
import scipy as sp
import time, sklearn, math
from sklearn.model_selection import train_test_split
import sklearn.datasets, sklearn.neighbors, sklearn.tree, sklearn.metricsdef sklearnDecisionTreeTest():#Step 1. Load the datasettempDataset = sklearn.datasets.load_breast_cancer()x = tempDataset.datay = tempDataset.target# Split for training and testingx_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2)#Step 2. Build classifiertempClassifier = sklearn.tree.DecisionTreeClassifier(criterion='entropy')tempClassifier.fit(x_train, y_train)#Step 3. Test#precision, recall, thresholds = sklearn.metrics.precision_recall_curve(y_test, tempClassifier.predict(x_test))tempAccuracy = sklearn.metrics.accuracy_score(y_test, tempClassifier.predict(x_test))tempRecall = sklearn.metrics.recall_score(y_test, tempClassifier.predict(x_test))#Step 4. Outputprint("precision = {}, recall = {}".format(tempAccuracy, tempRecall))sklearnDecisionTreeTest()

版本2. 自己重写重要函数

信息熵

#计算给定数据集的香农熵
def calcShannonEnt(paraDataSet):numInstances = len(paraDataSet)labelCounts = {}	#定义空字典for featVec in paraDataSet:currentLabel = featVec[-1]if currentLabel not in labelCounts.keys():labelCounts[currentLabel] = 0labelCounts[currentLabel] += 1shannonEnt = 0.0for key in labelCounts:prob = float(labelCounts[key])/numInstancesshannonEnt -= prob * math.log(prob, 2) #以2为底return shannonEnt

划分数据集

#dataSet 是数据集，axis是第几个特征，value是该特征的取值。
def splitDataSet(dataSet, axis, value):resultDataSet = []for featVec in dataSet:if featVec[axis] == value:#当前属性不需要reducedFeatVec = featVec[:axis]reducedFeatVec.extend(featVec[axis+1:])resultDataSet.append(reducedFeatVec)return resultDataSet

选择最好的特征划分

#该函数是将数据集中第axis个特征的值为value的数据提取出来。
#选择最好的特征划分
def chooseBestFeatureToSplit(dataSet):#决策属性不算numFeatures = len(dataSet[0]) - 1baseEntropy = calcShannonEnt(dataSet)bestInfoGain = 0.0bestFeature = -1for i in range(numFeatures):#把第i列属性的值取出来生成一维数组featList = [example[i] for example in dataSet]#剔除重复值uniqueVals = set(featList)newEntropy = 0.0for value in uniqueVals:subDataSet = splitDataSet(dataSet, i, value)prob = len(subDataSet) / float(len(dataSet))newEntropy += prob*calcShannonEnt(subDataSet)infoGain = baseEntropy - newEntropyif(infoGain > bestInfoGain):bestInfoGain = infoGainbestFeature = ireturn bestFeature

构建叶节点

#如果剩下的数据中无特征，则直接按最大百分比形成叶节点
def majorityCnt(classList):classCount = {}for vote in classList:if vote not in classCount.keys():classCount[vote] = 0classCount += 1;sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgette(1), reverse = True)return sortedClassCount[0][0]

创建决策树

#创建决策树
def createTree(dataSet, paraFeatureName):featureName = paraFeatureName.copy()classList = [example[-1] for example in dataSet]#Already pureif classList.count(classList[0]) == len(classList):return classList[0]#No more attributeif len(dataSet[0]) == 1:#if len(dataSet) == 1:return majorityCnt(classList)bestFeat = chooseBestFeatureToSplit(dataSet)#print(dataSet)#print("bestFeat:", bestFeat)bestFeatureName = featureName[bestFeat]myTree = {bestFeatureName:{}}del(featureName[bestFeat])featvalue = [example[bestFeat] for example in dataSet]uniqueVals = set(featvalue)for value in uniqueVals:subfeatureName = featureName[:]myTree[bestFeatureName][value] = createTree(splitDataSet(dataSet, bestFeat, value), subfeatureName)return myTree

分类和返回预测结果

#Classify and return the precision
def id3Classify(paraTree, paraTestingSet, featureNames, classValues):tempCorrect = 0.0tempTotal = len(paraTestingSet)tempPrediction = classValues[0]for featureVector in paraTestingSet:print("Instance: ", featureVector)tempTree = paraTreewhile True:for feature in featureNames:try:tempTree[feature]splitFeature = featurebreakexcept:i = 1 #Do nothingattributeValue = featureVector[featureNames.index(splitFeature)]print(splitFeature, " = ", attributeValue)tempPrediction = tempTree[splitFeature][attributeValue]if tempPrediction in classValues:breakelse:tempTree = tempPredictionprint("Prediction = ", tempPrediction)if featureVector[-1] == tempPrediction:tempCorrect += 1return tempCorrect/tempTotal

构建测试代码

def mfID3Test():#Step 1. Load the datasetweatherData = [['Sunny','Hot','High','FALSE','N'],['Sunny','Hot','High','TRUE','N'],['Overcast','Hot','High','FALSE','P'],['Rain','Mild','High','FALSE','P'],['Rain','Cool','Normal','FALSE','P'],['Rain','Cool','Normal','TRUE','N'],['Overcast','Cool','Normal','TRUE','P'],['Sunny','Mild','High','FALSE','N'],['Sunny','Cool','Normal','FALSE','P'],['Rain','Mild','Normal','FALSE','P'],['Sunny','Mild','Normal','TRUE','P'],['Overcast','Mild','High','TRUE','P'],['Overcast','Hot','Normal','FALSE','P'],['Rain','Mild','High','TRUE','N']]featureName = ['Outlook', 'Temperature', 'Humidity', 'Windy']classValues = ['P', 'N']tempTree = createTree(weatherData, featureName)print(tempTree)#print(createTree(mydata, featureName))#featureName = ['Outlook', 'Temperature', 'Humidity', 'Windy']print("Before classification, feature names = ", featureName)tempAccuracy = id3Classify(tempTree, weatherData, featureName, classValues)print("The accuracy of ID3 classifier is {}".format(tempAccuracy))def main():sklearnDecisionTreeTest()mfID3Test()main()