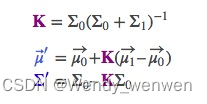---

前言

本文的主要内容是维纳滤波和卡尔曼滤波的介绍，包含匹配滤波器、维纳滤波器、维纳预测、卡尔曼滤波等内容。

---

一、滤波简介

我们观测到的信号都是受到噪声干扰的，如何最大限度地抑制噪声，将有用信号提取出来，是信号处理的基本问题。
信号处理的目的就是要得到不受干扰影响的真实信号。 相应的处理系统称为滤波器。
已知x(n), x(n-1), …, x(n-m)，估计以后时刻的信号值s(n+N)，N≥1，这样的估计问题称为预测问题；
已知x(n), x(n-1), …, x(n-m)，估计当前的信号值s(n)，称为过滤或滤波；
已知x(n), x(n-1), …, x(n-m)，估计过去的信号值s(n-N)，N≥1，称为平滑或内插。
以估计结果与信号真值之间的误差的均方值最小作为最佳准则。最小均方误差准则(MMSE, Minimum Mean Square Error)。
维纳(Wiener)滤波与卡尔曼(Kalman)滤波就是用来解决从噪声中提取信号的过滤或预测问题。
维纳滤波器的求解，要求知道随机信号的统计分布规律，即相关函数或功率谱密度。
维纳滤波的最大缺点是仅适用于平稳随机信号。
匹配滤波器、维纳滤波器是两种常用的最优滤波器。匹配滤波器能够使滤波器的输出达到最大的信噪比；维纳滤波器能够使滤波器的输出的均方估计误差最小。

---

二、匹配滤波器

匹配滤波器的信噪比：

信噪比有最大值。

滤波器的输出达到最大信噪比时，滤波器的幅频特性与信号的幅频特性相等，或者说二者匹配。
将白噪声情况下的信噪比最大的线性滤波器称为匹配滤波器。

匹配滤波器对波形相同而幅度不同的时延信号具有适应性。
信号通过匹配滤波器，相当于对信号作相关处理。

---

三、维纳滤波器

1.时域求解

假定滤波器的输入和期望响应均为广义平稳随机过程，且已知其二阶统计特性，则可根据最小均方误差准则求得最优滤波器的参数，这种滤波器称为维纳滤波器。
维纳滤波器实现了统计意义上最优的对未知系统的逼近。

均方误差达到最小的充分必要条件是误差信号与输入信号正交，这就是正交性原理。
正交性原理为判断滤波器是否工作于最佳状态提供了一个数学方法。
当滤波器工作于最佳状态时，输出信号与误差信号也是正交的。
期望信号、估计值(滤波器输出)与估计偏差(误差信号)的几何关系如下图所示。

当滤波器处于最佳工作状态时，估计值加上估计偏差等于期望信号，即：

因此在滤波器处于最佳状态时，估计值y(n)的能量总是小于等于期望信号d(n)的能量。

2.维纳-霍夫方程

维纳-霍夫方程定义如下：

求解维纳-霍夫方程可得最佳权系数，根据权系数是有限个还是无限个，可分别设计FIR型和IIR型的维纳滤波器。

依次带入k的值到上式中有：

再进行如下定义：

写成矩阵形式如下：

求逆得到：

也就是说，如果知道观测数据与期望信号的互相关函数和观测数据的自相关函数时，通过矩阵求逆运算，可得到FIR型维纳滤波器的系统函数h(k)。
最小均方误差：

3.系统函数求解例题

4.离散维纳滤波器的Z域解

若不考虑滤波器的因果性，维纳-霍夫方程可以写为：

设d(n)=s(n)，对上式两边做Z变换有：

这里的下标opt就是optimal的缩写，即最佳的意思。
假设信号与噪声不相关，即r_sv(m)=0 (其中x(n)=s(n)+v(n))，则有：

从而

当噪声为0时，信号全部通过；当信号为0时，噪声全部被抑制掉，因此维纳滤波的确有滤除噪声的能力。

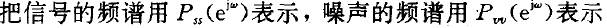
非因果维纳滤波器的传输函数的幅频特性如下。

把信号转化为白噪声的过程称为白化，对应的滤波器称为白化滤波器。
非因果维纳滤波器的复频域最佳解的一般表达式：

非因果维纳滤波器的最小均方误差：

因果维纳滤波器的复频域最佳解的一般表达式：

因果维纳滤波器的最小均方误差：

因果维纳滤波器设计的步骤：

5.最佳解例题

---

四、维纳预测

1.预测的定义

预测就是根据过去的观测数据来估计将来的数据。
信号内部是存在关联性的，预测就是利用数据之间的关联性，根据一部分数据推知其余的数据。
数据之间的关联性越密切，预测越准确。对于白噪声，由于数据之间没有关联性，所以无法预测。
系统是有惯性的，平稳随机信号可以看作是白噪声激励线性系统的输出，此时的输入是无关联的白噪声，而输出是有关联的信号。
在维纳预测中，有：

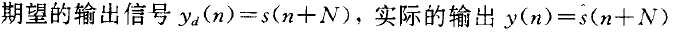
故非因果维纳预测器的最佳解为：

因果维纳预测器的最佳解为：

2.纯预测

x(n) = s(n) + v(n)，v(n)是噪声，当v(n) = 0，期望信号为s(n+N)，N≥1，此种情况称为纯预测。
纯预测情况下的输入信号功率谱及维纳滤波器的最佳解分别为：

纯预测例题如下：

由上面的例题可以知道，纯预测维纳滤波器是一个比例放大器。

3.一步线性预测的时域解

已知x(n-1), x(n-2)…, x(n-p)，预测x(n)，称为一步线性预测。
Yule-Walker 方程：

方程的特点：除了第一个方程外，其余都是齐次方程；与维纳-霍夫方程相比，不需要知道观测数据x(n)与期望信号s(n)的互相关函数。
一步线性预测的例题如下：

其中涉及到的Z变换如下：

---

五、卡尔曼滤波

1.概念及定义

维纳滤波器要求已知信号和噪声的统计特性，仅适用于处理一维、平稳随机信号。
为了解决非平稳、多输入、多输出随机信号的估计问题，卡尔曼提出了递推最优估计理论。
递推法计算过程：

由递推法可知，n时刻的估计值可以由n-1时刻的估计值和当前观测值加权确定。
卡尔曼递推算法根据前一个时刻状态的估计值和当前时刻的观测数据，递推估计当前时刻的状态值。适合于计算机处理，可以处理多维、非平稳随机信号。
卡尔曼滤波的特点：
1.算法是递推的，且状态空间法采用在时域内设计滤波器的方法，因而适用于多维随机过程的估计；离散型卡尔曼算法适用于计算机处理。
2.用递推法计算，不需要知道全部过去的值，用状态方程描述状态变量的动态变化规律，因此信号可以是平稳的，也可以是非平稳的，即卡尔曼滤波适用于非平稳过程。
3.卡尔曼滤波采取的误差准则仍为估计误差的均方值最小。
卡尔曼滤波状态方程和量测方程：

或者

卡尔曼递推公式：

卡尔曼滤波就是利用观测数据y(k)估计状态向量x(k)的最佳值。卡尔曼滤波和维纳滤波都是采用均方误差最小准则。

2.例题分析

3.维纳滤波与卡尔曼滤波的异同

维纳滤波要求已知观测数据的自相关函数和观测数据与期望信号的互相关函数，通过建立滤波器进行滤波处理得到期望信号的估计值；卡尔曼滤波要求已知观测数据与期望数据之间的数学模型（状态方程和量测方程），通过递推算法得到期望信号的估计值。
维纳滤波的解是以H(z)或h(n)的形式给出，卡尔曼滤波的解是以状态变量的估计值给出，二者都采用均方误差最小准则, 但卡尔曼滤波有一个过渡过程，在过渡期间其结果与维纳滤波不完全相同，但过渡过程结束达到稳态后，二者的处理结果是相同的，前提是处理平稳信号时。

---

总结

以上就是维纳滤波和卡尔曼滤波的所有内容了，注意对比记忆，本文参考的课本是丁玉美数字信号处理-时域离散随机信号处理。