Generalized Linear Models广义线性模型
指数家族(The exponential family)
指数家族是指一类概率分布,其具有指数模式。需要注意,这是一类概率分布,不是特指某个概率分布,因此指数分布只有固定的格式,根据参数不同,会生成不同的分布。
指数家族分布定义
若一个随机变量y的分布被称为指数家族分布,那么其需要满足:
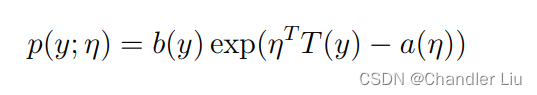
由以上可看出,p(y)是被η参数化的,所以随着η的不同,就会生出不同的分布。
指数家族分布例子一——伯努利分布
我们可以对伯努利分布进行变化,具体如下:
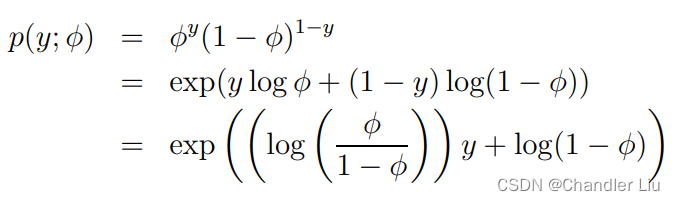
由以上可看出,上面的变换后的结果,符合指数家族的定义,其中η = log(φ/(1 − φ))
指数家族分布例子二——高斯分布
以均值为µ,方差为1的高斯分布为例(注意,在线性回归模型中我们已经推导,方差对于最终的θ及h(θ)无影响,所以这里简化推导过程,把方差设为1)
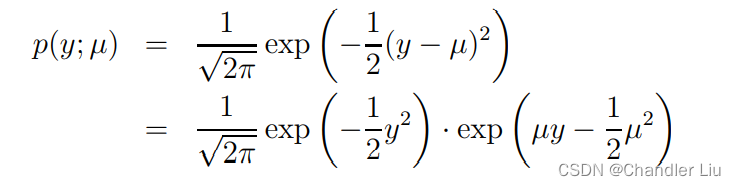
由此可见,η = µ
指数家族分布其他例子
还有泊松分布,指数分布等也为指数家族分布的其他例子,不在此做推导了
使用GLM构造机器学习模型
利用GLM来构建机器学习模型的步骤及前提
假设P1:假定y | x; θ ∼ ExponentialFamily(η).
假设P2:给定训练集x,我们的目标是预测E[T(y)](注:T(y)一般等于y),即我们要使h(x) = E[y|x]
假设P3:指定η = θ^Tx,即η与x为线性关系(本条可视为基于经验的最佳设计选择)
按照上方1-3步骤,可逐步构建相应的GLM机器学习模型。
利用GLM来构建机器学习模型的示例一——线性回归模型
基于本文上方推导,我们知道高斯分布属于指数家族,且满足η = µ。所以:
STEP1:根据假设P1,我们假定某一目标值y服从于正态分布(具体假定服从于什么分布需要看y的实际意义,若y>0,则用泊松分布等可能更合适~),即
y~N (µ,σ^2)
STEP2:根据假设P2,我们有:
hθ(x) = E[y|x; θ] = µ = η = θ^T x.
STEP3:由此,我们构建出一个线性机器学习模型,如下:
y=hθ(x)=θ^T x
利用GLM来构建机器学习模型的示例二——逻辑斯蒂回归模型
逻辑斯蒂回归适用于伯努利概率分布,因为目标y仅有两种取值0或1。
基于本文上方推导,我们知道伯努利概率分布也属于指数家族,且满足φ = 1/(1 + e
^(−η))。所以:
STEP1:根据假设P1,我们假定某一目标值y服从于伯努利分布,即
y|x; θ ∼ Bernoulli(φ)
STEP2:根据假设P2,我们有:
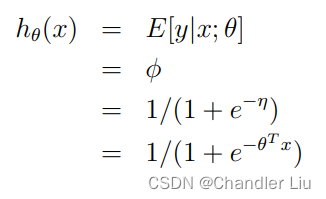
STEP3:由此,我们构建出一个线性机器学习模型,如下:
y=hθ(x)= 1/(1 + e^ (−θ^T x))
利用GLM来构建机器学习模型的示例三——Softmax 回归模型
假定目标集可取值为k元,即y∈{1,2,…,k},则y属于多元分布,现在根据构造GLM的步骤,构造Softmax回归模型
STEP1:假设y的每种取值的概率为φ1,…,φk(需要注意这些概率值之间不相互独立,因为概率的归一性,有φk=1-(φ1+…+φk-1))
STEP2:下面我们来构造T(y),定义如下:
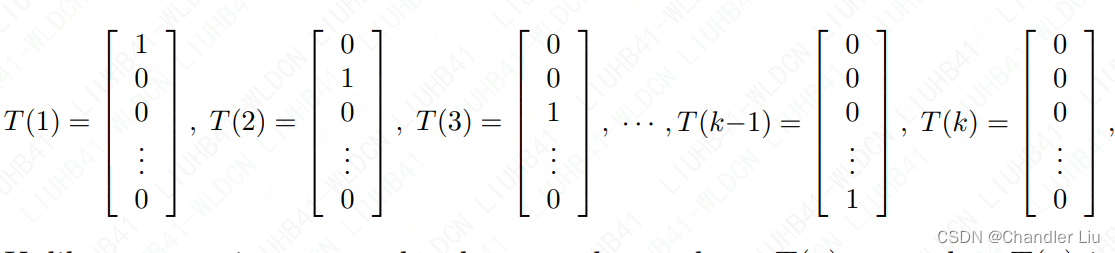
(注意这里的T(y)为n-1维向量)
STEP3:定义一个函数1{·} ,其含义为1{True} = 1, 1{False} = 0。我们用(T(y))i代表T(y)的第i个元素(i∈{1,2,…,k-1}),则有:
E[(T(y))i] =P(Y=y)(T(y))i= φi(注意T(y)i=0 if y≠i)
STEP4:证明多元分布为指数家族分布,即符合假设一:
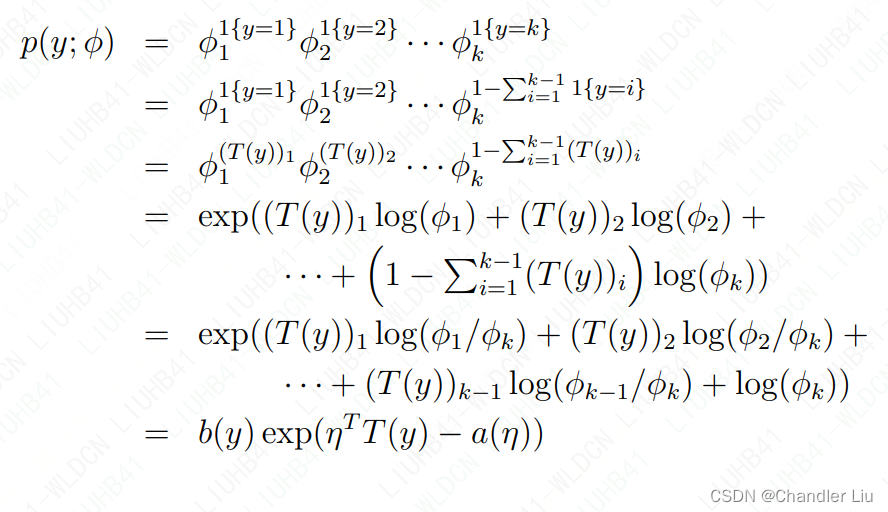
其中
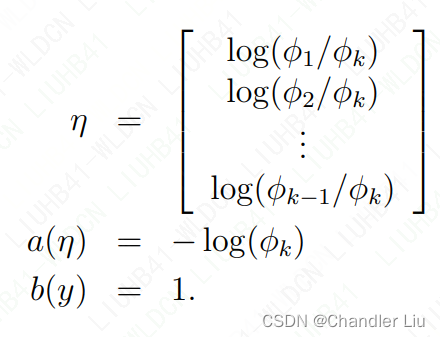
由以上可观察得: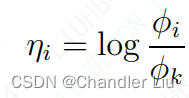
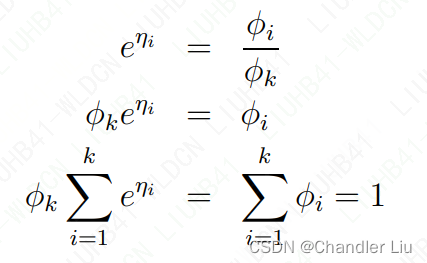
进一步推导,有:
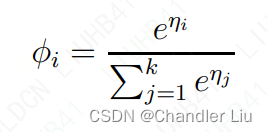
以上公式即为softmax function。
STEP5:根据假设3,我们有ηi = (θi^T)x (for i = 1, . . . , k − 1),即线性相关。
由此,我们有:
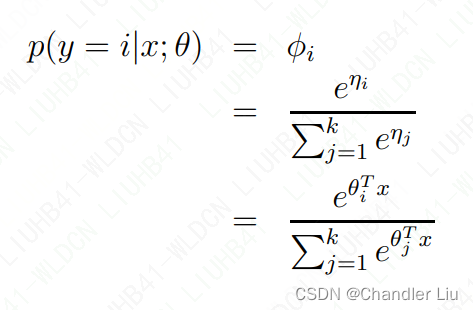
再根据假设二,我们有:

以上过程即为softmax回归
使用softmax回归
那么针对m组训练集,如何使用softmax回归获得具体的参数呢?我们有构造最大似然函数:
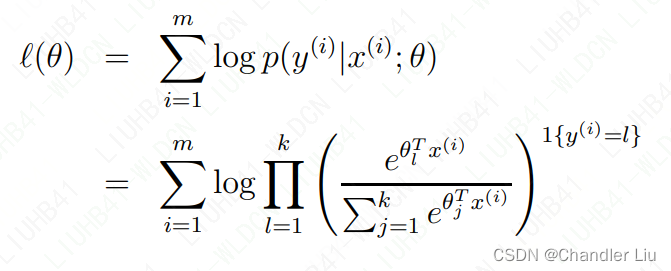
之后可用梯度下降等方法,来最大化l(θ),求出对应的θ