🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
混合模型(Mixture Model)
混合模型是一个可以用来表示在总体分布(distribution)中含有 K 个子分布的概率模型,换句话说,混合模型表示了观测数据在总体中的概率分布,它是一个由 K 个子分布组成的混合分布。混合模型不要求观测数据提供关于子分布的信息,来计算观测数据在总体分布中的概率。
高斯模型
单高斯模型
当样本数据 X 是一维数据(Univariate)时,高斯分布遵从下方概率密度函数(Probability Density Function):
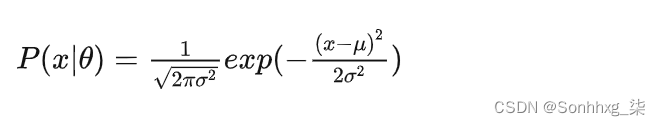
其中 μ 为数据均值(期望), σ 为数据标准差(Standard deviation)。
当样本数据 X 是多维数据(Multivariate)时,高斯分布遵从下方概率密度函数:
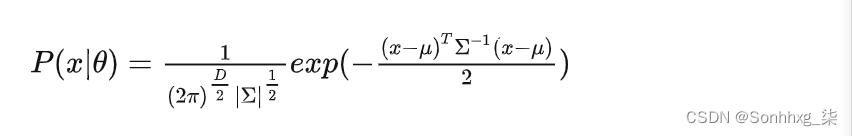
其中, μ 为数据均值(期望), Σ 为协方差(Covariance),D 为数据维度。
高斯混合模型
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量(Hidden variable)。一般来说,一个混合模型可以使用任何概率分布,这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。
举个不是特别稳妥的例子,比如我们现在有一组狗的样本数据,不同种类的狗,体型、颜色、长相各不相同,但都属于狗这个种类,此时单高斯模型可能不能很好的来描述这个分布,因为样本数据分布并不是一个单一的椭圆,所以用混合高斯分布可以更好的描述这个问题,如下图所示:
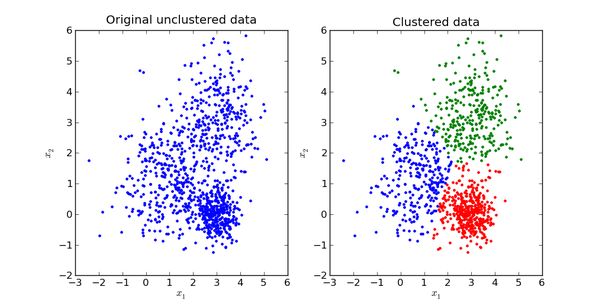
图中每个点都由 K 个子模型中的某一个生成
首先定义如下信息:

模型参数学习
对于单高斯模型,我们可以用最大似然法(Maximum likelihood)估算参数 θ 的值,

这里我们假设了每个数据点都是独立的(Independent),似然函数由概率密度函数(PDF)给出。

由于每个点发生的概率都很小,乘积会变得极其小,不利于计算和观察,因此通常我们用 Maximum Log-Likelihood 来计算(因为 Log 函数具备单调性,不会改变极值的位置,同时在 0-1 之间输入值很小的变化可以引起输出值相对较大的变动):
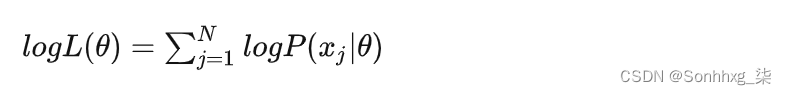
对于高斯混合模型,Log-Likelihood 函数是:
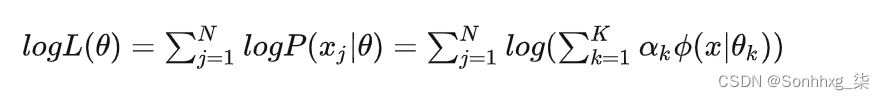
如何计算高斯混合模型的参数呢?这里我们无法像单高斯模型那样使用最大似然法来求导求得使 likelihood 最大的参数,因为对于每个观测数据点来说,事先并不知道它是属于哪个子分布的(hidden variable),因此 log 里面还有求和,对于每个子模型都有未知的 αk,μk,σk ,直接求导无法计算。需要通过迭代的方法求解。
EM 算法
EM 算法是一种迭代算法,1977 年由 Dempster 等人总结提出,用于含有隐变量(Hidden variable)的概率模型参数的最大似然估计。
每次迭代包含两个步骤:
- E-step:求期望 E(γjk|X,θ) for all j=1,2,...,N
- M-step:求极大,计算新一轮迭代的模型参数
这里不具体介绍一般性的 EM 算法(通过 Jensen 不等式得出似然函数的下界 Lower bound,通过极大化下界做到极大化似然函数),只介绍怎么在高斯混合模型里应用从来推算出模型参数。
通过 EM 迭代更新高斯混合模型参数的方法(我们有样本数据 x1,x2,...,xN 和一个有 K 个子模型的高斯混合模型,想要推算出这个高斯混合模型的最佳参数):
- 首先初始化参数
- E-step:依据当前参数,计算每个数据 j 来自子模型 k 的可能性

至此,我们就找到了高斯混合模型的参数。需要注意的是,EM 算法具备收敛性,但并不保证找到全局最大值,有可能找到局部最大值。解决方法是初始化几次不同的参数进行迭代,取结果最好的那次。
高斯混合模型代码实现
from __future__ import division, print_function
import math
from sklearn import datasets
import numpy as npfrom mlfromscratch.utils import normalize, euclidean_distance, calculate_covariance_matrix
from mlfromscratch.utils import Plotclass GaussianMixtureModel():""一种用于确定数据样本之间分组的概率聚类方法。参数:-----------k: 整数算法将形成的簇数。最大迭代次数:整数如果确实如此,算法将运行的迭代次数在此之前不收敛。公差:浮动如果从一次迭代到下一次迭代的结果的差异是小于这个值我们就说算法已经收敛。"""def __init__(self, k=2, max_iterations=2000, tolerance=1e-8):self.k = kself.parameters = []self.max_iterations = max_iterationsself.tolerance = toleranceself.responsibilities = []self.sample_assignments = Noneself.responsibility = Nonedef _init_random_gaussians(self, X):""" 随机初始化高斯 """n_samples = np.shape(X)[0]self.priors = (1 / self.k) * np.ones(self.k)for i in range(self.k):params = {}params["mean"] = X[np.random.choice(range(n_samples))]params["cov"] = calculate_covariance_matrix(X)self.parameters.append(params)def multivariate_gaussian(self, X, params):""" 可能性 """n_features = np.shape(X)[1]mean = params["mean"]covar = params["cov"]determinant = np.linalg.det(covar)likelihoods = np.zeros(np.shape(X)[0])for i, sample in enumerate(X):d = n_features # dimensioncoeff = (1.0 / (math.pow((2.0 * math.pi), d / 2)* math.sqrt(determinant)))exponent = math.exp(-0.5 * (sample - mean).T.dot(np.linalg.pinv(covar)).dot((sample - mean)))likelihoods[i] = coeff * exponentreturn likelihoodsdef _get_likelihoods(self, X):""" 计算所有样本的似然度 """n_samples = np.shape(X)[0]likelihoods = np.zeros((n_samples, self.k))for i in range(self.k):likelihoods[:, i] = self.multivariate_gaussian(X, self.parameters[i])return likelihoodsdef _expectation(self, X):""" 计算 responsibility """# 计算X属于不同簇的概率weighted_likelihoods = self._get_likelihoods(X) * self.priorssum_likelihoods = np.expand_dims(np.sum(weighted_likelihoods, axis=1), axis=1)# Determine responsibility as P(X|y)*P(y)/P(X)self.responsibility = weighted_likelihoods / sum_likelihoods# Assign samples to cluster that has largest probabilityself.sample_assignments = self.responsibility.argmax(axis=1)# Save value for convergence checkself.responsibilities.append(np.max(self.responsibility, axis=1))def _maximization(self, X):""" 更新参数和先验 """# 遍历簇并重新计算均值和协方差for i in range(self.k):resp = np.expand_dims(self.responsibility[:, i], axis=1)mean = (resp * X).sum(axis=0) / resp.sum()covariance = (X - mean).T.dot((X - mean) * resp) / resp.sum()self.parameters[i]["mean"], self.parameters[i]["cov"] = mean, covariance# 更新权重n_samples = np.shape(X)[0]self.priors = self.responsibility.sum(axis=0) / n_samplesdef _converged(self, X):""" Covergence if || likehood - last_likelihood || < tolerance """if len(self.responsibilities) < 2:return Falsediff = np.linalg.norm(self.responsibilities[-1] - self.responsibilities[-2])# print ("Likelihood update: %s (tol: %s)" % (diff, self.tolerance))return diff <= self.tolerancedef predict(self, X):""" 运行 GMM 并返回集群索引 """# 随机初始化高斯self._init_random_gaussians(X)# 运行 EM 直到收敛或最大迭代for _ in range(self.max_iterations):self._expectation(X) # E-stepself._maximization(X) # M-step# 检查收敛if self._converged(X):break# 进行新的分配并返回它们self._expectation(X)return self.sample_assignments