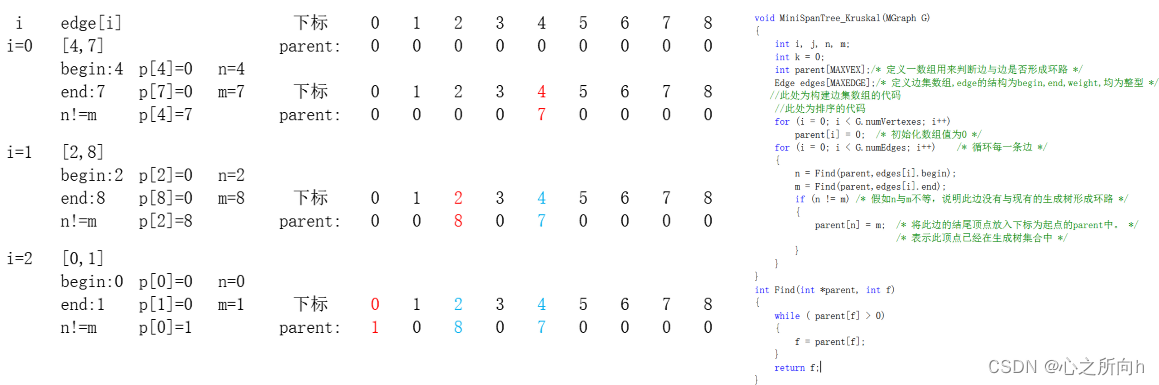
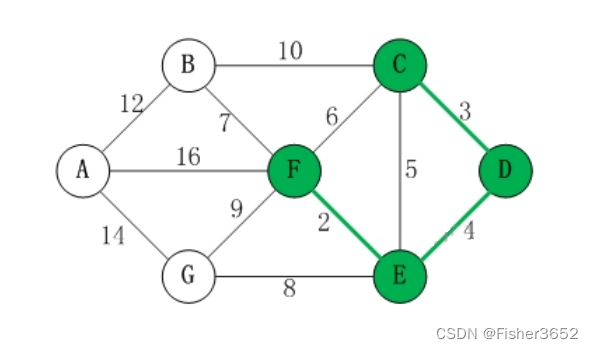
Kruskal

首先我们约定 n为节点数，m为边数

一、概念

Kruskal算法主要用于解决Minimum Spanning Trees(最小生成树)问题。

二、基本思想

先选择权值较小的边，检查是否存在回路，然后继续选择，直到选择了 $n - 1$ 的边结束。

三、模板代码

const int N=1005;//Nodes Count
const int M=2010;//Edges Count
int p[N];//p[i]记录节点 i 的父节点
int n;//顶点数
int res=0;
struct Edge
{int a;//Start Point of the edgeint b;//End Point of the edgeint v;//The Value of the edge
}edge[M];
int find(int x)//找到x的父节点
{return p[x]==x ? x : p[x]=find(p[x]);//等价于以下代码/*if(p[x]==x)//如果其父节点是其本身(它就是最nb的节点)return x;else p[x]=find(p[x]);//令x的父节点p[x]去寻找其父节点并赋值(路径压缩)       return find(p[x]); */
}
void merge(int x,int y)//将含x,y的两个集合合并成一个集合
{p[find(x)]=find(y);
}
bool cmp(Edge x,Edge y)//排序函数
{return x.v<y.v;    
}
int main()
{for (int i = 0; i < N; i++) p[i]=i;//初始每个节点的父节点都为自己//Input every edges info/* Code */sort(edge,edge+idx,cmp);//idx:边数int cnt=0;//记录已选择边的数量for (int i = 0; i < idx; i++)//枚举选择每条边{int x=edge[i].a,y=edge[i].b;if(find(x)!=find(y)) //没有成环{cnt++;merge(x,y);res+=edge[i].v;if(cnt==n-1) break;//如果题意可能不存在最小生成树，请依题意修改}}cout << res << endl;
}