版权声明:这就是我的文章啊
这一个算法。有点厉害。
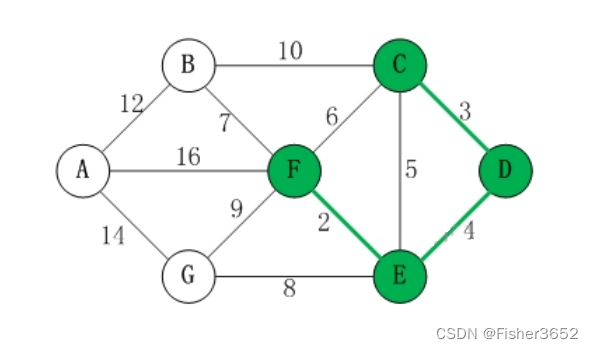
首先,输入一个图,然后求它的最小生成树(即一条最短的链,联通N个顶点)。
(这就是图)
好的,然后,我们首先观察这个图,发现他的答案是15.
非常的神奇。
每一个顶点在一开始都是一个独立的集合,因为他没有和任何人连边。
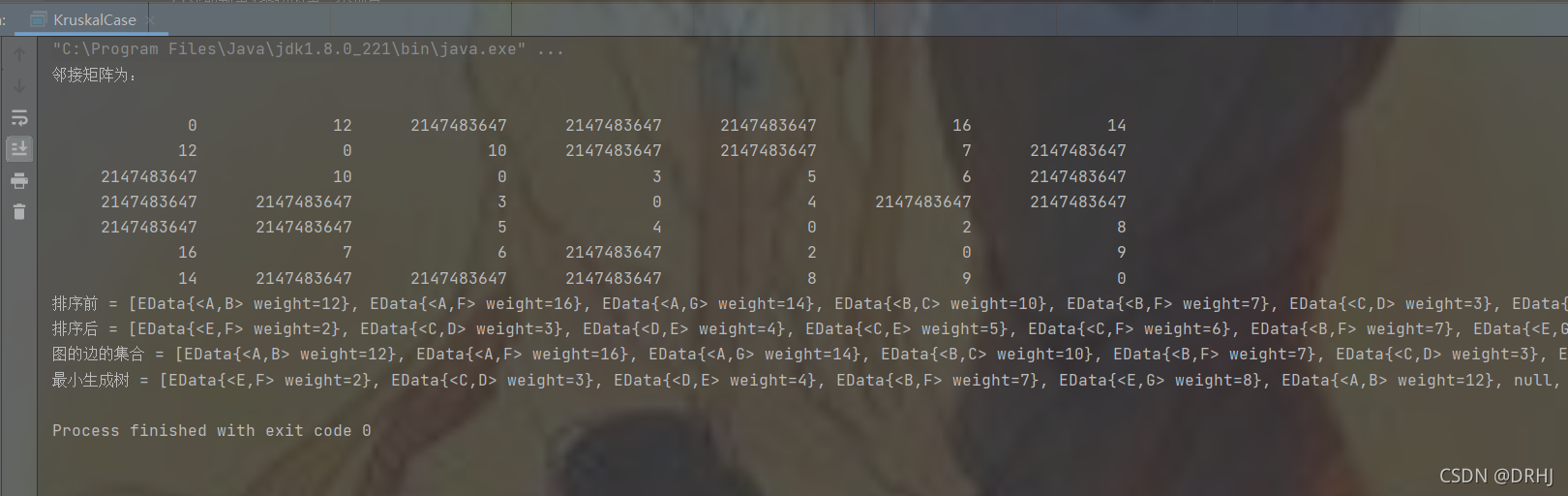
接着,我们将这10条边,按边权排序(这是为了可以选到最优的边)
我们开始选边了。首先,我们发现(V1,V3)这条边的边权是目前图中最小的。
况且他们两个都代表着一个独立的集合(1,3)。于是我们就可以把他们两个愉快地连边。
接着是(V4,V6)顺利的连边
接着是(V2,V5)顺利的连边
接着是(V3,V6)顺利的连边
好的现在的集合情况是1:(V1,V3,V4,V6)2:(V2,V5)
接着到(V1,V4)。
这个虽然是目前最短的,但是我们不可以将它连边。
为什么?
因为他们是同一个集合的。
为什么同一集合就不能连边呢?
因为,连了边,也是白连,(V1,V4)本来就已经是联通的了,再连一条边没有任何意义,反而会增加答案数。
于是我们舍去这条边不取。
当我们连上(V2,V3)之后,整个图就联通了。
你们可能会有个问题:怎么判断(Vx,Vy)是同一个集合的呢?
这要用到并查集。详情请看我的另一篇博客
var f:array[1..1001] of longint;
a:array[0..500001,1..3] of longint;
i,j,k,n,m,x,y,c:longint;
s:int64;
procedure qsort(l,r:longint);
var x,y,m:longint;
begin
x:=l;
y:=r;
m:=a[(l+r) div 2,3];
repeat
while a[x,3]<m do inc(x);
while a[y,3]>m do dec(y);
if x<=y then
begin
a[0]:=a[x];
a[x]:=a[y];
a[y]:=a[0];
inc(x);dec(y);
end;
until x>y;
if l<y then qsort(l,y);
if r>x then qsort(x,r);
end;
function fu(z:longint):longint;
var x,y:longint;
begin
y:=z;
while y<>f[y] do y:=f[y];
while z<>y do
begin
x:=f[z];
f[z]:=y;
z:=x;
end;
exit(y);
end;
begin
readln(n,m);
for i:=1 to m do
begin
readln(x,y,c);
a[i,1]:=x;
a[i,2]:=y;
a[i,3]:=c;
end;
qsort(1,m);
for i:=1 to n do f[i]:=i;
s:=0;
for i:=1 to m do
begin
j:=fu(a[i,1]);
k:=fu(a[i,2]);
if j<>k then
begin
s:=s+a[i,3];
f[j]:=k;
end;
end;
writeln(s);
end.