Karger 算法简析

概述

Karger算法是解决最小割问题的随机算法。当然，它是一个近似算法。虽然是近似算法，但它速度快，实现简单。

算法细节

一个直观的想法是，对于一个无向图$G$，为找到它的最小割$(S,T)$， 随机选择一条边，将这条边无限变短直到两关联结点重合，然后继承除被缩短的边以外其余所有边，删去自环。

重复以上过程，直到图中只剩下两个结点。这两个结点代表的就是这样的一个最小割。

注意

只能删去自环边。
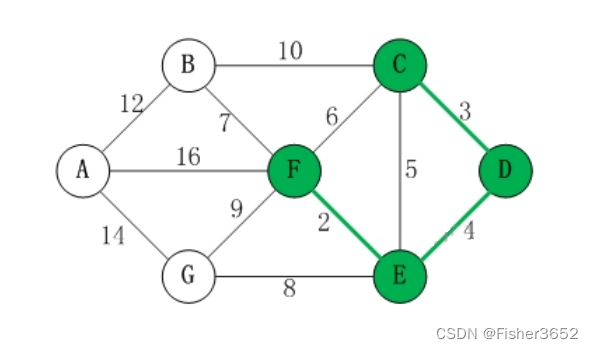
举个例子，如下的无向图。

          1/  |/    |2------3|      ||      |4------5

合并结点1， 3后，得到

 _______
/       \
2-------1, 3
|        |
|        |
4--------5

注意，此时（1， 2）， （3， 2）两条边虽然共同组成了一个环，但它们没有一个是自环，因此必须保留。
接下来假设我们合并1， 2， 得到下图：

________
\       |\      |\     |1, 2, 3/    |/      |
4-------5

注意此时1， 2， 3形成了自环，因此删去自环边，所以这一步骤结束后的图应当是

   1, 2, 3/     |/       |
/        |
4--------5

总结

在日前计算对于某一给定无向图该算法获得最优解的概率时，由于忽略自环的精确定义导致计算错误。特此记录。