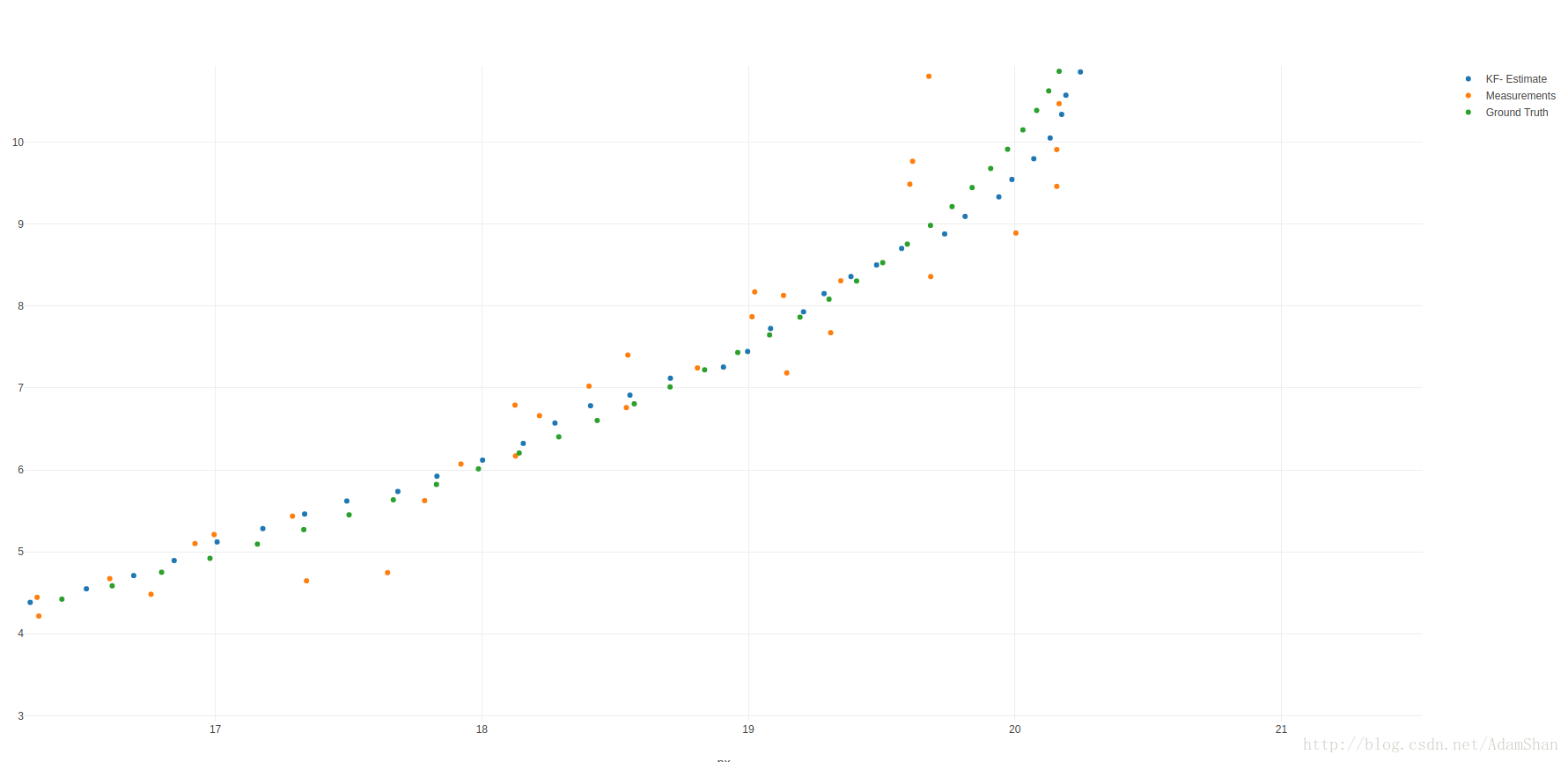
背景

二维标准kalman滤波仿真，绘制了噪声、跟踪状态和误差图，并且加入了攻击的代码部分，需要在第一个状态量的量测值中设置攻击的时候，将attack变量设置为1，会在20-40,60-80时刻加入相应攻击，攻击变量为atk可以自己设置。

代码

%Project: 基本二维Kalman
%Author: Jace
%Data: 2021/10/06
%--------------------准备---------------------
close all;
clear all;
clc;
%------------------初始化参数---------------------N=100;%设定采样点数，即持续时长%噪声相关参数
P0=0.01;%初始状态噪声协方差
p=zeros(2,2,N);
Q=[0.01,0.0;0.0,0.01];%设定系统噪声
R=[0.1,0.0;0.0,0.1];%设定观测噪声
w=sqrt(Q)*randn(2,N);
v=sqrt(R)*randn(2,N);%攻击相关参数
attack=0;%攻击1是否开启
atk=sqrt(2.6)*randn(1,N);%攻击%系统模型参数
A=[1.002,0;0,0.998];%状态转移矩阵
H=[1,0;0,1];%局部量测1量测矩阵%----------------初始化分配空间-------------------------
%真实状态值初始化
x=zeros(2,N);%物体真实状态值（分配空间），2*N维矩阵
x(:,1)=[10+P0*randn(1);20+P0*randn(1)];%物体初始真实状态值%误差协方差初始化
p(:,:,1)=[1,0;0,1];%误差协方差初始值%两个传感器量测值初始化
z=zeros(2,N);%量测值
z(:,1)=H*x(:,1);%观测真实值初始值,二维向量%各滤波器估计值初始化
xkf=zeros(2,N);%全局估计状态
xkf(:,1)=x(:,1);%全局估计状态初始化为第一列的列向量I=eye(2);%2*2单位矩阵%----------------NRD------------------------
for k=2:N%系统模型x(:,k)=A*x(:,k-1)+w(k);%量测模型，标量z(:,k)=H*x(:,k)+v(k);%注入攻击if attack==1if k>=20&&k<=40||k>=60&&k<=80z(1,k)=z(1,k)+atk(k);endend%----------------标准Kalman过程------------------------%估计误差协方差预测更新p_pre=A*p(:,:,k-1)*A'+Q;%增益矩阵预测更新K=p_pre*H'/(H*p_pre*H'+R);%状态值预测更新x_pre=A*xkf(:,k-1);%状态值量测更新xkf(:,k)=x_pre+K*(z(:,k)-H*x_pre);%估计误差协方差量测更新p(:,:,k)=(I-K*H)*p_pre;
end%--------------------------误差计算--------------------------------
%初始化
messure_err_z1=zeros(1,N);
messure_err_z2=zeros(1,N);
kalman_err_x1=zeros(1,N);
kalman_err_x2=zeros(1,N);
for k=1:N%量测误差messure_err_z1(k)=abs(z(1,k)-x(1,k));messure_err_z2(k)=abs(z(2,k)-x(2,k));%Kalman估计偏差kalman_err_x1(k)=abs(xkf(1,k)-x(1,k));kalman_err_x2(k)=abs(xkf(2,k)-x(2,k));
end%噪声图
figure;
subplot(2,2,1)
plot(w(1,:));xlabel('采样时间');ylabel('噪声');
title('第1状态值过程噪声');
subplot(2,2,2)
plot(w(2,:));xlabel('采样时间');ylabel('噪声');
title('第2状态值过程噪声');
subplot(2,2,3)
plot(v(1,:));xlabel('采样时间');ylabel('噪声');
title('第1状态值第1传感器量测噪声');
subplot(2,2,4)
plot(v(2,:));xlabel('采样时间');ylabel('噪声');
title('第2状态值第2传感器量测噪声');%局部滤波器1
figure;
hold on,box on;
plot(x(1,:),'-k.');
plot(z(1,:),'-b.');
plot(xkf(1,:),'-r.');
legend('第1状态值','第1量测值','第1状态量Kalman估计值');
xlabel('采样时间');ylabel('位置');
title('状态1跟踪');%局部滤波器2
figure;
hold on,box on;
plot(x(2,:),'-k.');
plot(z(2,:),'-b.');
plot(xkf(2,:),'-r.');
legend('第2状态值','第2量测值','第2状态量Kalman估计值');
xlabel('采样时间');ylabel('位置');
title('状态2跟踪');%局部滤波器1误差
figure;
hold on,box on;
plot(messure_err_z1,'-b.');
plot(kalman_err_x1,'-g.');
legend('量测','Kalman估计');
xlabel('采样时间');ylabel('误差');
title('滤波器1误差');%局部滤波器2误差
figure;
hold on,box on;
plot(messure_err_z2,'-b.');
plot(kalman_err_x2,'-g.');
legend('量测','Kalman估计');
xlabel('采样时间');ylabel('误差');
title('滤波器2误差');%量测值记录
figure;
hold on,box on;
plot(z(1,:));
plot(z(2,:));
xlabel('采样时间');ylabel('数值');
legend('量测1','量测2');
title('量测值记录');

效果