计算布尔二叉树的值

难度：简单

给你一棵 完整二叉树 的根，这棵树有以下特征：

• 叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。
• 非叶子节点 要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR ，3 表示逻辑与 AND 。

计算 一个节点的值方式如下：

• 如果节点是个叶子节点，那么节点的 值 为它本身，即 True 或者 False 。
• 否则，计算 两个孩子的节点值，然后将该节点的运算符对两个孩子值进行 运算 。

返回根节点 root 的布尔运算值。

完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。

叶子节点 是没有孩子的节点。

示例 1：

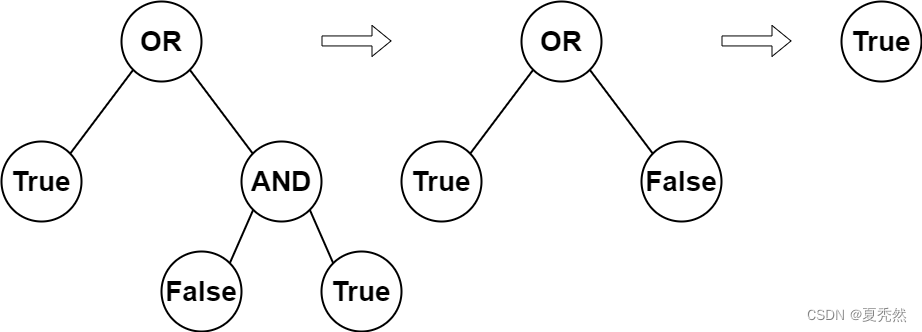
输入：root = [2,1,3,null,null,0,1]
输出：true
解释：上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ，所以我们返回 true 。

示例 2：

输入：root = [0]
输出：false
解释：根节点是叶子节点，且值为 false，所以我们返回 false 。

递归

思路：

• 若当前节点是叶子节点的时候，判断是否为1返回结果，相当于转换为 True 和 False。
• 若当前节点不是叶子节点，则递归查询其左右子节点，并以当前节点的逻辑对左右节点做运算。

复杂度分析：

• 时间复杂度： $O(n)$，递归过程中将整个树遍历一遍。
• 空间复杂度： $O(n)$，递归过程中需要将利用到栈，由于是完整二叉树最小深度为 $logn$，即完全二叉树，最大深度为 n/2，即单向左或右衍生，因此复杂度为 $O(n)$。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def evaluateTree(self, root: Optional[TreeNode]) -> bool:if root.val == 0 or root.val == 1:return root.val == 1left, right = self.evaluateTree(root.left), self.evaluateTree(root.right)return left or right if root.val == 2 else left and right

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/evaluate-boolean-binary-tree