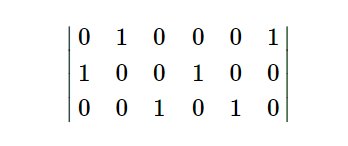LeetCode 1360

时间之间隔几天

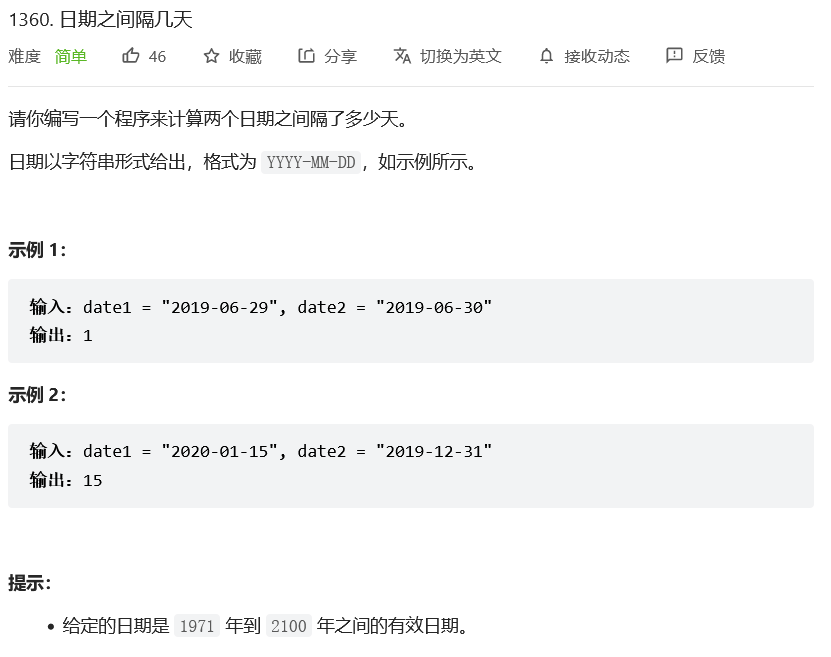
两个日期之间没有大小关系，可能第 1 个日期大，可能第 2 个日期大，需要同时处理两种情况

1971.1.1 → date1 一共过了 days1 天

1971.1.1 → date2 一共过了 days2 天

| day1 - day2 | 就是答案，因为不知道哪个数大，只要返回差的绝对值即可

把问题转换为：1971.1.1 → 2019.6.29 一共过了多少天？

①先计算 1971.1.1 → 2018.12.31一共过了多少天，一年一年走平年 365 天，闰年 366 天

②2018.12.31→ 2019.5.31 一个月一个月走每个月的天数是固定的（2 月特判）O( 12 ) 平年 28天闰年 29天

③2019.5.31→ 2019.6.29 一天一天走最后日期是多少就走多少天 O( 1 )

同样方式求1971.1.1 → date2 过了多少天，两个相减，取绝对值即可

sscanf的使用

sscanf() 是从一个字符串中读进与指定格式相符的数据

scanf()是从终端输入读进与指定格式相符的数据

参考：sscanf的用法_badogyang的博客-CSDN博客_sscanf

class Solution {
public:int daysBetweenDates(string date1, string date2) {//返回两个天数差的绝对值return abs(get(date1)-get(date2));}//判断闰年bool is_leap(int year){//1.不是整百年数 % 4 == 0 就是闰年 2.是整百年数 % 400 == 0return year % 100 && year % 4 == 0 || year % 400 == 0;}//月份判断-> 用数组存储每个月的天数 下标为 0 的不使用int m_days[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};//求计算过了多少天的函数int get(string date){int year,month,day;//把 date 中的年月日提取出来sscanf(date.c_str(),"%d-%d-%d",&year,&month,&day);//记录最终答案一共过了多少天int days = 0;//从年份开始走for(int i = 1971;i < year;i++ ) day += 365 + is_leap(i); //如果当前年是闰年需要 + 1//一个月一个月走-> 特判二月for(int i = 1;i < month;i++){if(i == 2) days += 28 + is_leap(year); //是二月份判断是不是闰年else days += m_days[i];                //不是二月份直接加上天数}//加上天数return days + day;}
};

验证二叉树

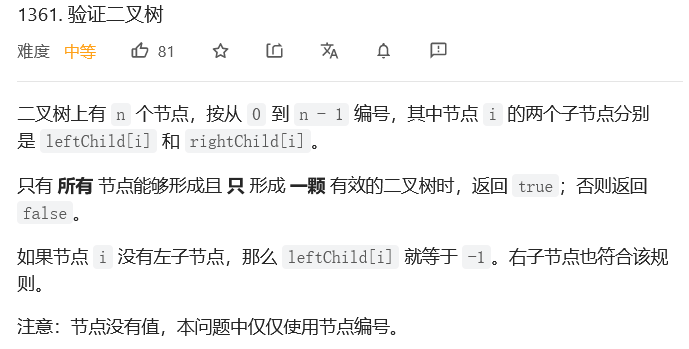
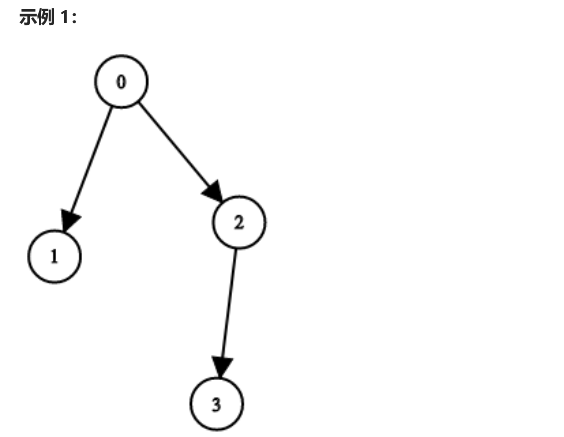
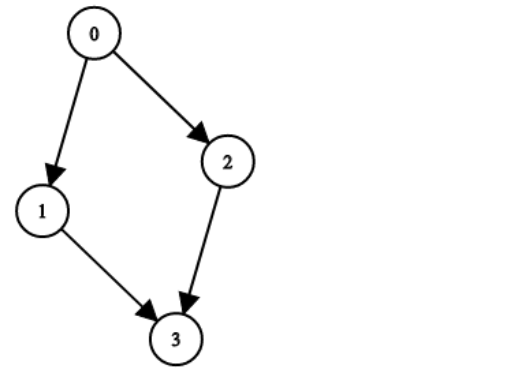
题目中给出 n 个节点，n 个节点的下标是 [ 0 ] ~ [ n - 1] 给出存储二叉树的方式，n 个节点的下标是 [ 0 ] ~ [ n - 1 ]，给出第 i 个的节点的两个孩子节点的下标

如果某个孩子节点不存在就是 -1，判断给出的信息能否构成一棵合法的二叉树

示例1：序号 0 的左孩子是 1，leftChild[ 0 ] = 1 右孩子是 2，rightChild[ 0 ] = 2；

序号 1 的左孩子是 -1，leftChild[ 1 ] = -1 右孩子是 -1，rightChild[ 1 ] = -1

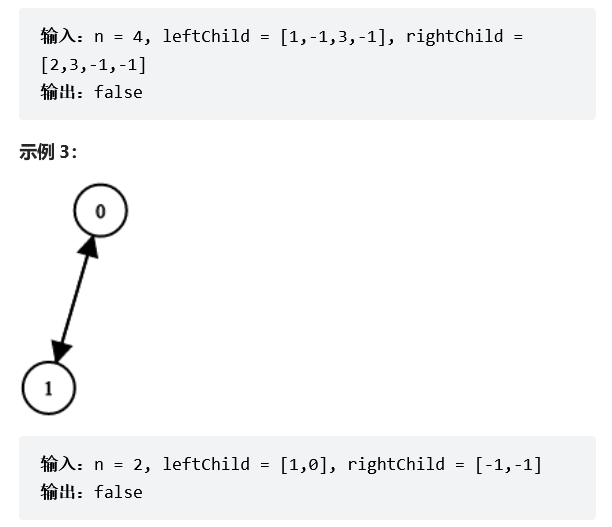
示例3：形成了一个环，不满足要求

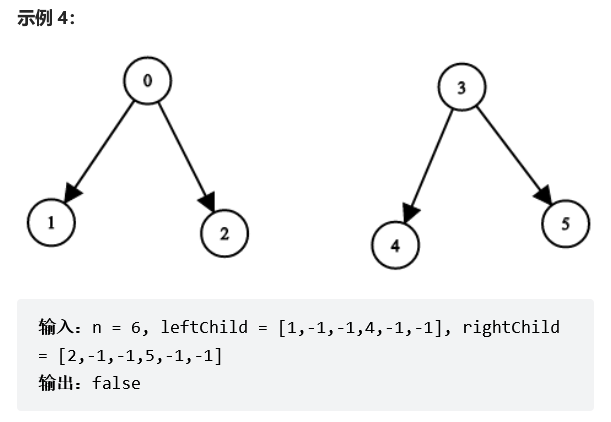
示例4：有两棵二叉树，不满足要求只能有一棵二叉树

①找到根节点(如果有多个根节点就是不合法的) 任意一个→ 没有父节点的节点：入度为 0 的点、没有节点指向它求所有点的度数，找到一个度数为 0 的点，当做根节点，从根节点进行 BFS | DFS 遍历，判断两个条件是否满足

②从根节点开始，沿着它的所有边做一个遍历 DFS | BFS 条件：遍历过程中是否有矛盾：搜索到的点之前搜到过、往回搜→ 有没有搜索到重复的点，每一个点都是被一个点搜到的，每一个点只有一个父节点满足是一棵树

③可能有两棵树，需要判断是不是所有点都能被搜到，如果所有点都能被搜到说明只有一棵树；如果某些点没有被搜到，说明这些点不在这棵树中，至少存在两棵树满足只有一棵树

只要满足是一棵树，就一定是一棵二叉树，因为题目规定树节点的孩子节点的数目最多只有 2

class Solution {
public:bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {//统计度数-> 入度的数量vector<int> d(n);//求每个点的入度-> 遍历所有的边for(int i = 0;i < n;i++ ){//如果leftChild | rightChild不是-1说明是有左|右孩子 左|右孩子有入度 if(leftChild[i] != -1) d[leftChild[i]] ++;if(rightChild[i] != -1) d[(rightChild[i])] ++;  }//找根节点 int root = 0;//判断有没有根节点 度数为 0的点是根节点 d[root] != 0 root++ while(root < n && d[root]) root++; //没有根节点-> 不是一棵树if(root == n) return false;//否则用BFS从根节点开始遍历所有点//判断所有点是否被遍历一遍vector<bool> st(n);//根节点被遍历st[root] = true;//BFS需要准备一个队列queue<int> q;//把根节点插到队列中q.push(root);while(q.size()){//队列不为空 每次取出队头int t = q.front();q.pop();//遍历孩子int sons[] = {leftChild[t],rightChild[t]};//循环遍历所有的孩子for(auto s : sons){//如果s不为-1 说明是有孩子的if(s != -1){//如果s被遍历了说明被重复遍历了不满足第一个条件if(st[s]) return false;//否则说明没有被遍历过-> 标记被遍历 然后把这个点插到队列中去st[s] = true;q.push(s);}}}//判断所有点是否被遍历过-> 如果某一个点没有被遍历过不满足第二个条件for(auto state : st)if(!state)return false;//满足所有条件return true;}
};

最接近的因数

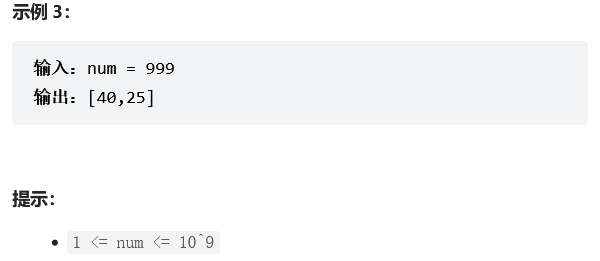
①两个整数乘积等于 num + 1 或 num + 2

②两个整数差的绝对值最小

一定只有一组解，不需要考虑多组解的情况

假设存在 y2 - y1 == x2 - x1，由于两组的差是相等的，设 y2、y1 组比 x2、x1 组大，y1、y2 最小取 x1 + 1，x2 + 1

由于 num 是大于等于 1 的数，所以 num + 1 和 num + 2 都是正整数

x1，x2 最小是 1，y1 × y2 一定大于等于 x1 × x2 + 3，如果 x1 × x2 = num + 1，那么 y1 × y2 不可能等于 num + 1

问题一定有解，因为可以分解为 1 × ( num + 1）

示例1：8，找两个整数使得它们的乘积 9 或者是 10

9 = 1 × 9

= 3 × 3

10 = 1 × 10

= 2 × 5

两个数不需要同时枚举，可以只枚举其中的一个，一个确定之后，另外一个直接除就可以了，只枚举较小的那个，枚举 1 ~ √ num + 1

或者1 ~ √ num + 2，x1 越小，x2 越大，因此，在枚举的时候从√ num + 2 开始枚举到 1，第一次枚举到的满足条件的解一定是最小的

结果，后面的值 x1会更小，x2 会更大，它们之间的差会更大

num + 1 与 num + 2 一定互质(相邻两个整数互质)，所以 x1 不可能同时是两个数的约数，只能是其中某一个的约数

先判断 num + 1，num + 1 会比 num + 2 差更小

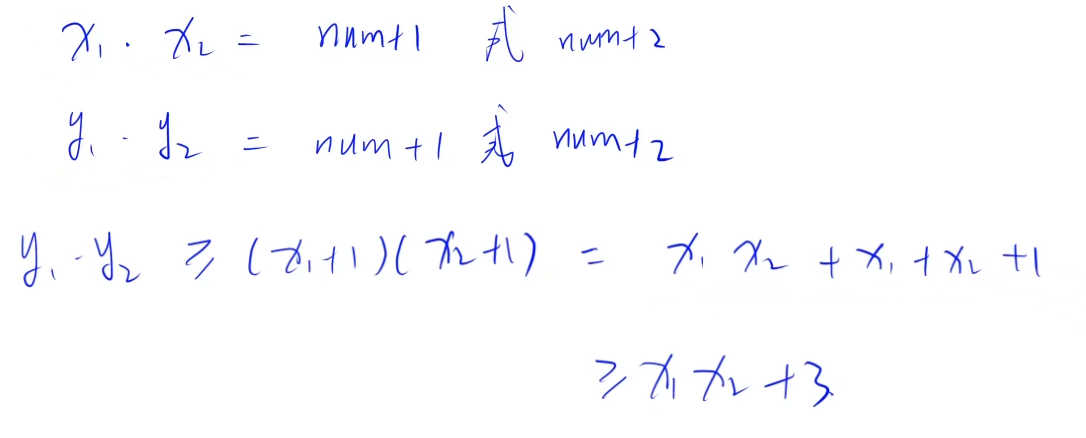
class Solution {
public:vector<int> closestDivisors(int num) {//从大到小循环for(int i = sqrt(num + 2); i;i--){if((num + 1) % i == 0) return {i, (num + 1) / i};if((num + 2) % i == 0) return {i, (num + 2) / i};}//避免语法错误return { };}
};