1360G 1900

题意：对一个长度为m高度为n的全为零二维数组进行操作也就是ar[n][m], 令其每列横行1的个数为a,每排纵行的1的个数为b，
如下所示、

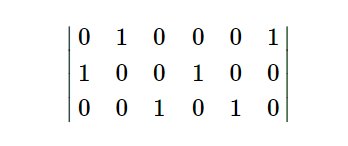
该数组的a=2，b=1，问你是否存在这么一个ar[n][m]数组使得其满足a和b的要求，如果存在打印“YES”且打印出这个数组，若不存在，则打印“NO”。
思路：首先判断这个数组是否存在，这个是相对来说比较简单的，可以知道这个数组的和也就是所有的横行的1相加的和或者说所有纵行的1相加的和，SUM = an=bm，如果不满足这个条件肯定是不存在这个二维数组的，但如果相等，那么就存在。
对于存在的数组中‘1’的排列，可以对于每行的‘1’的排列进行平移a个位置，举个例子
对于3 6 2 1的数组可以
1 1 0 0 0 0
0 0 1 1 0 0
0 0 0 0 1 1
这样排列，如果排列超出了这个数组的长度限制则对m取余也就是每行的格数。最后不难得到答案
具体实现看代码

int main(){IOS;int t;cin>>t;while(t--){int n, m, a, b;cin>>n>>m>>a>>b;int ar[100][100];memset(ar, 0, sizeof(ar));if(n*a!=b*m){cout<<"NO"<<endl;continue;}else cout<<"YES"<<endl;int x = 0;for(int i = 0; i < n; i++){for(int j = 0; j < a; j++){ar[i][x] = 1;x++;x = x%m;}}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){cout<<ar[i][j];}cout<<endl;}}return 0;
}