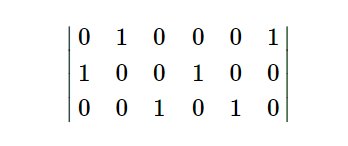题意

求要在一个正方形内构造两个长方形，长和宽分别为 $a,b$
问这个正方形面积最小为多少

做法

显然如果将两个叠起来放，必然选择较小的那条边作为叠起来的宽度
但这个时候还要比较另一条边的大小，选取最大的值
也就是说 $max(2\ast b,a)$ 即其中一种方式构成的最小正方形的边长，$max(2\ast a,b)$ 就是另一种
两者取 $min$ 即可

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define min(a,b)    ((a)>(b)?(b):(a))
#define max(a,b)    ((a)>(b)?(a):(b))
const int maxn = 50 + 5;int main() {int T;scanf("%d", &T);while(T--) {int a, b;scanf("%d%d", &a, &b);a = min(max(a, 2 * b), max(2 * a, b));printf("%d\n", a * a);}return 0;
}

目录

题意

要构造 $A,B$ 两个集合
使 $abs(max(A)-min(B))\to min$

做法

由于没有要求集合元素个数， $A,B$ 两个集合我们可以自由选择
那么只要选取 两个差值绝对值最小的数 就好了
把这两个差值绝对值最小的两个数 的较大一个数放到集合 $A$，较小的一个放到集合 $B$
然后其他的数也可以不用管了，或者说比扔到 $A$ 这个集合的数小的可以扔到集合 $A$
同理比扔到 $B$ 这个集合的数大的可以扔到集合 $B$

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define min(a,b)    ((a)>(b)?(b):(a))
#define max(a,b)    ((a)>(b)?(a):(b))
const int inf = 0x3f3f3f3f;
const int maxn = 50 + 5;int a[maxn];int main() {int T;scanf("%d", &T);while(T--) {int n;scanf("%d", &n);for(int i = 1; i <= n; ++i)	scanf("%d", &a[i]);sort(a + 1, a + 1 + n);int ans = inf;for(int i = 2; i <= n; ++i)ans = min(ans, a[i] - a[i - 1]);printf("%d\n", ans);}return 0;
}

目录

题意

如果两个数 $x$ 和 $y$ 具有相同的奇偶性（除以 $2$ 时的余数相同），
或者如果 $x-y=1$ ，我们称它们为相似的数 $x$ 和 $y$
问这个长度为 $n$ 的数组能否完全构造成相似数
保证 $n$ 是偶数

做法

首先当 奇数的个数 为 偶数时，肯定可以
剩下的情况就是多了一个奇数，那么对应的也会多出一个偶数
只要排序遍历一遍数组，查找是否有两个相邻的数就可以了
因为相邻的数必然是一个奇数一个偶数，正好符合多出来的两个数

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define min(a,b)    ((a)>(b)?(b):(a))
#define max(a,b)    ((a)>(b)?(a):(b))
const int inf = 0x3f3f3f3f;
const int maxn = 50 + 5;int a[maxn];int main() {int T;scanf("%d", &T);while(T--) {int n, c = 0;scanf("%d", &n);for(int i = 1; i <= n; ++i) {scanf("%d", &a[i]);if(a[i] % 2)    c += 1;}if(c % 2 == 0) {puts("YES");}else{bool flag = false;sort(a + 1, a + 1 + n);for(int i = 2; i <= n; ++i) {if(a[i] - a[i - 1] == 1) {flag = true;break;}}printf("%s\n", flag ? "YES" : "NO");}}return 0;
}

目录

题意

Polycarp 想买 $n$ 把铲子，商店卖的铲子有 $k$ 种包装，第 $i$ 种包装由 $i$ 把铲子组成
他买的时候只能选择一种包装
问最少需要买多少包

做法

显然我们要选择的是 $n$ 的因子中，小于等于 $k$ 的最大因子
开根号从大的开始遍历，第一个符合条件的就是

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define min(a,b)    ((a)>(b)?(b):(a))
#define max(a,b)    ((a)>(b)?(a):(b))
const int inf = 0x3f3f3f3f;
const int maxn = 50 + 5;int a[maxn];int main() {int T;scanf("%d", &T);while(T--) {int n, k;scanf("%d%d", &n, &k);if(k >= n) {puts("1");}else{int x = sqrt(n * 1.0), ans = n;for(int i = x; i > 0; --i) {if(n % i == 0) {if(i <= k)      ans = min(ans, n / i);if(n / i <= k)  ans = min(ans, i);}}printf("%d\n", ans);}}return 0;
}

目录

题意

左边和右边都有炮台可以放炮，上面的炮台向下放炮，左边的炮台向右放炮
每次放的炮都会到最边界或者有 $1$ 的地方前
给出最终的图，$1$ 是炮停到的地方
问是否能得到这个图

做法

如果不是在右边界或者下边界的话
只要判断为 $1$ 的该位置的 右边 或者 下边 是否存在 $1$ 即可

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 50 + 5;char s[maxn][maxn];int main() {int T;scanf("%d", &T);while(T--) {int n; bool flag = true;scanf("%d", &n);for(int i = 1; i <= n; ++i) {scanf("%s", s[i] + 1);s[n + 1][i] = s[i][n + 1] = 0;} for(int i = 1; i <= n; ++i) {for(int j = 1; j <= n; ++j) {if(i == n || j == n)    continue;if(s[i][j] == '1' && s[i + 1][j] != '1' && s[i][j + 1] != '1') {flag = false;break;}}}printf("%s\n", flag ? "YES" : "NO");}return 0;
}

目录

题意

问是否存在一个串，使得该串与给定的 $n$ 个串不同的地方只有一个

做法

$n,m\le 10$，范围很小
因此可以给定最后结果串先与 $s[0]$ 相同
然后暴力遍历结果串的每一个位置
暴力遍历每个位置更改成 $26$ 个字母的其中一个
判断更改后是否可以满足条件
时间复杂度为 $O(26\ast 10\ast 10\ast 10\ast T)$

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 10 + 5;char s[maxn][maxn];
char res[maxn];
int n, m;bool check() {for(int i = 0; i < n; ++i) {int cnt = 0;for(int j = 0; j < m; ++j)cnt += (res[j] == s[i][j] ? 0 : 1);if(cnt > 1) return false;} return true;
}int main() {int T;scanf("%d", &T);while(T--) {bool flag = false;scanf("%d%d", &n, &m); res[m] = 0;for(int i = 0; i < n; ++i)  scanf("%s", s[i]);for(int i = 0; i < m; ++i)  res[i] = s[0][i];for(int i = 0; i < m; ++i) {for(int j = 'a'; j <= 'z'; ++j) {res[i] = j;if(check()) {flag = true;break;}}if(flag)    break;res[i] = s[0][i];}printf("%s\n", flag ? res : "-1");}return 0;
}

目录

题意

有一个长 $n$ 宽 $m$ 的矩形，要使得每行有 $a$ 个 $1$，每列有 $b$ 个 $1$
是否存在这样的图

做法

首先是去除不可能的情况
在行填充时，必然会对列产生一定的影响；同理列填充的时候也会对行产生影响
观察样例可以发现，其实是跟比例有关
当 $m/a==n/b$ 的时候，是会存在解的
当然这个公式中 $a,b$ 都不能为 $0$
可以移项一下，变成 $m\ast b==n\ast a$，这样就可以处理 $a,b$ 为 $0$ 的情况了
$a,b$ 中只有一个为 $0$ 显然是不可能存在的情况

接下来处理填充
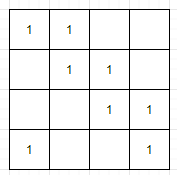
尝试自己构造第四个样例 $4$ $4$ $2$ $2$，可以得到下图
可以发现其实只要连续填充行所需要的个数 $a$，然后每次偏移一定的偏移量，就可以得到最后的图

问题是偏移量的计算

偏移是为了使列满足需要的个数 $b$，也就是为了使得每一列都可以填充到
又每次偏移的时候，行都会向下移动一行
也就是 偏移量 $\ast$ 行 $\%m==0$
$n$ 次偏移后正好 $m$ 列每列遍历到的次数都是一样的

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 50 + 5;int res[maxn][maxn];int main() {int T;scanf("%d", &T);while(T--) {int n, m, a, b;// puts("");scanf("%d%d%d%d", &n, &m, &a, &b);if(m * b != n * a)  puts("NO");else{puts("YES");int k;memset(res, 0, sizeof(res));for(k = 1; k < m; ++k)if(k * n % m == 0)break;// printf("%d\n", k);for(int i = 0, x = 0; i < n; ++i, x += k) {for(int j = 0; j < a; ++j) {res[i][(j + x) % m] = 1;}}for(int i = 0; i < n; ++i) {for(int j = 0; j < m; ++j)printf("%d", res[i][j]);puts("");}}}return 0;
}

目录

题意

长度为 $n$，全为 $0,1$ 的字符串
现在拿走 $m$ 个串后
问大小处在最中间（即中位数）的串是哪个串
如果是在两个数中间，则取较小的一个数

做法

首先将这些串都转化为十进制的数
由于 $m$ 最大为 $100$
只需要将原本的中位数分别往左右的 $100$ 个数，或者更多存入动态数组中
每次删除对应位置的数
最后的得到的数组中，数组的中位数也就是要求的中位数
最后输出的时候再转为二进制

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 60 + 5;char s[maxn];
vector<ll> v;ll getT(int m) {ll x = 0, y = 1ll;for(int i = m - 1; i >= 0; --i, y <<= 1ll)x += (s[i] == '0' ? 0 : y);return x;
}int main() {int T;scanf("%d", &T);while(T--) {int n, m; v.clear();scanf("%lld%d", &n, &m);ll k = (1ll << (m - 1));  // 中位数for(int i = -110; i < 110; ++i)v.push_back(k + i);ll x;for(int i = 0; i < n; ++i) {scanf("%s", s); x = getT(m);if(x < v[0])v.erase(v.begin());else if(x > v.back())v.erase(v.end() - 1);elsev.erase(find(v.begin(), v.end(), x));}x = v[(v.size() - 1) / 2];for(int i = m - 1; i >= 0; --i, x >>= 1ll)s[i] = x % 2 + '0';printf("%s\n", s);}return 0;
}