小朋友们好，大朋友们好！

我是猫妹，一名爱上Python编程的小学生。

和猫妹学Python，一起趣味学编程。

今日主题

汉诺塔

古印度大梵天传说

Python玩转汉诺塔

递归

汉诺塔

汉诺塔(Hanoi)是一个著名的益智游戏，也称为“大盘子游戏”或“回转木马”。

游戏的目标是将一组大小不同的盘子从一个柱子移动到另一个柱子上，但是每次只能移动一个盘子，并且大的盘子不可以放在小的盘子上面。

具体来说，有三根柱子，分别标有 A、B、C 的名称。

一开始，A 柱子上有 n 个盘子，编号为 1 到 n。

玩家需要将这些盘子从 A 柱子移动到 C 柱子上。

移动的方法是先将较小的盘子从 A 柱子移动到 B 柱子上，然后将较大的盘子从 A 柱子移动到 C 柱子上，最后将较小的盘子从 B 柱子移动到 C 柱子上。

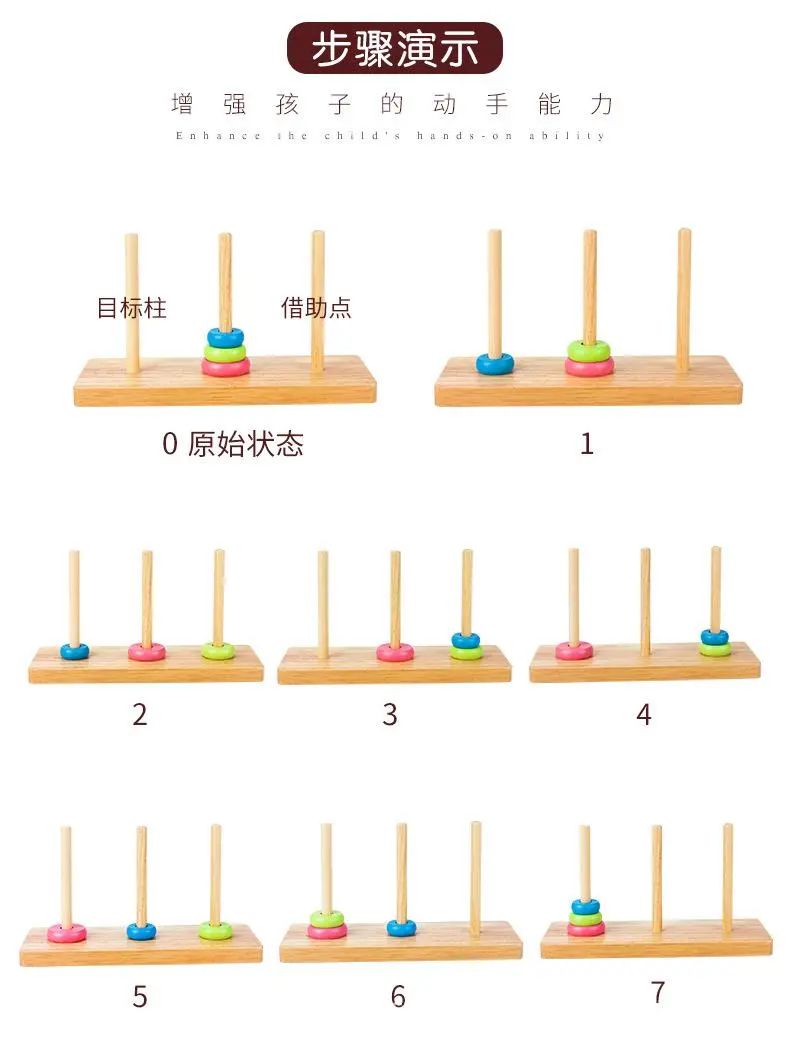
这个游戏看起来很简单，但是实际上需要进行多次移动才能完成。因为每次只能移动一个盘子，所以在进行移动时需要考虑所有可能的情况，以避免出现错误。

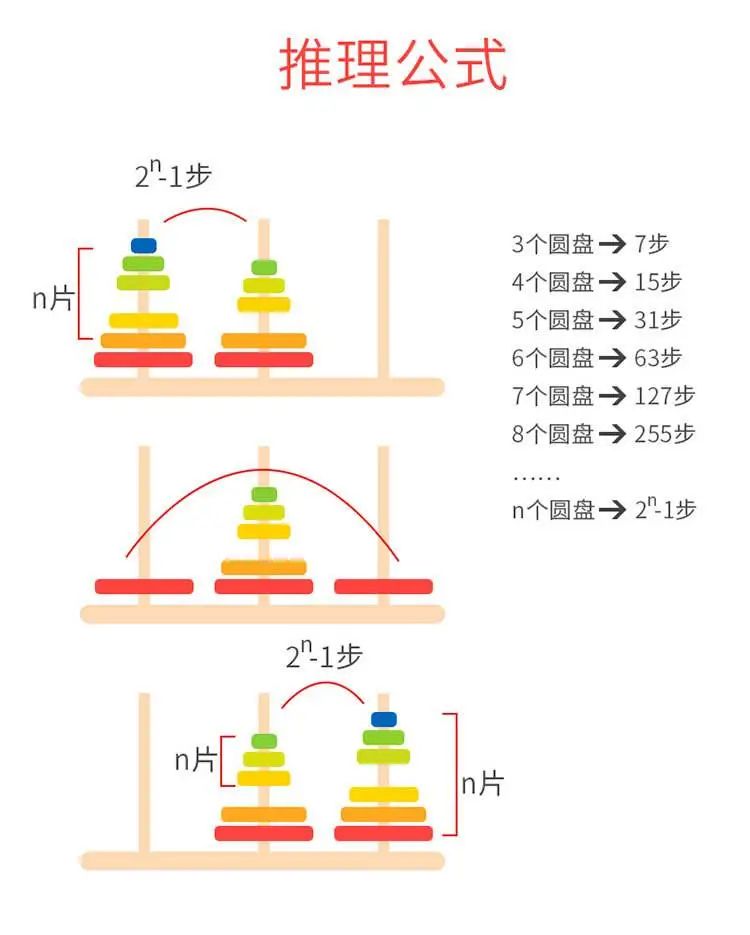
汉诺塔是一种经典的益智游戏，可以锻炼人们的思维能力和逻辑推理能力。它也被广泛应用于教育和培训领域，作为一种有效的学习和教学工具。

古印度大梵天传说

相传印度主神大梵天在创造世界的同时，也造了三根金刚石柱子。

其中一根柱子上放着64个大小均不相同的圆盘。大梵天命令婆罗门将这64个圆盘按照从大到小的顺序移动到另一根柱子上，在移动的过程中始终要保持大盘在下，小盘子在上。

这其实是一种时间的象征，因为按照这个规则，将64个圆盘移动到另一个圆柱上，在时间上来说几乎是不可能的，需要的时间可能比宇宙诞生的时间还要长，具体为什么？一会你就明白了。

Python玩转汉诺塔

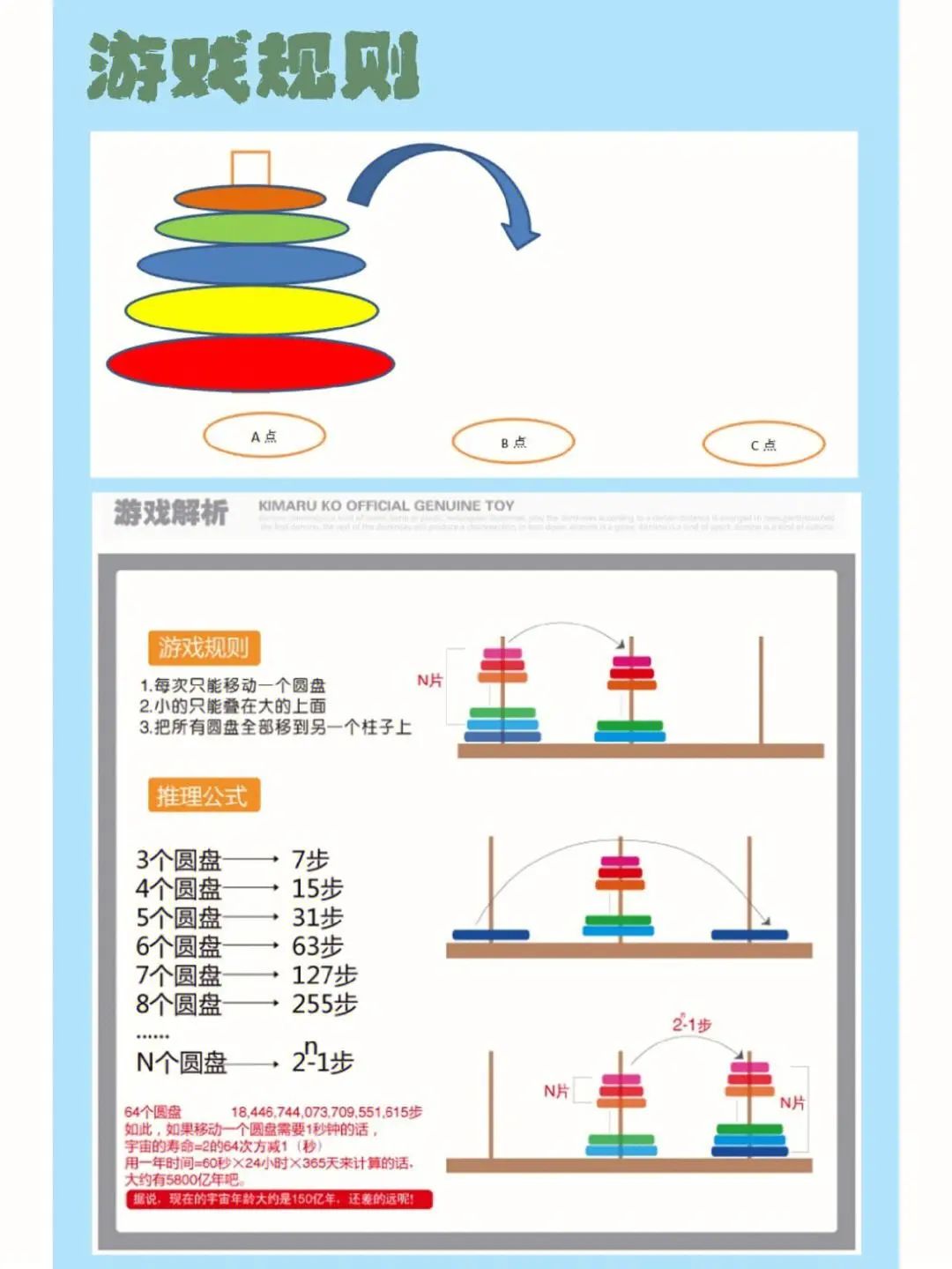
移动策略：

1.将(n-1)阶从A移动到B。

2.将n阶从A移动到C。

3.将(n-1)阶从B移动到C。

Python代码实现：

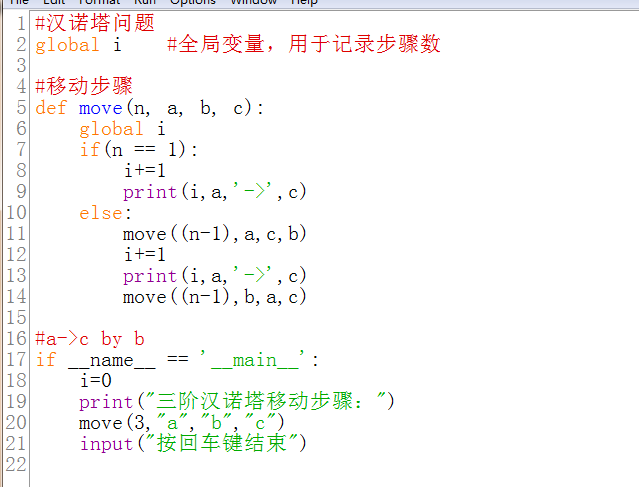
5849亿年

64阶需要移动次数为2**64-1=18446744073709551615

假设一秒移动一次，那么需要584942417355.072年。

大概需要5849亿年。

宇宙也不过才100多亿年。

假设从那时候开始玩，离完成还需要很多很多年，估计玩到人类灭绝还玩不完。

递归

在Python中，递归是一种函数调用自身的技术。当一个函数在其定义中调用自身时，就称为递归函数。

递归通常用于解决可以被分解为相同问题的子问题的问题。

例如，计算阶乘就是一个递归的例子。

当我们计算n的阶乘时，我们可以将其表示为1 * n!,其中n!是n的阶乘。

当我们计算4的阶乘时，我们可以写成1 * 4! = 1 * 24 = 24。

这是因为，当我们计算3的阶乘时，我们可以将其表示为3 * 2 * 1 = 6,然后将6乘以3得到18,这就是3的阶乘。

同样地，当我们计算2的阶乘时，我们可以将其表示为2 * 1 = 2,这就是2的阶乘。

因此，当我们计算4的阶乘时，我们可以写成4! = 4 * 3 * 2 * 1 = 24。

在Python中，递归函数需要满足一些条件才能正常工作。

首先，递归函数必须有一个结束条件，否则它将无限循环下去。

其次，递归函数必须明确处理所有可能的分支情况，否则它可能会出现错误或崩溃。

最后，递归函数必须能够正确地返回结果，否则它将无法达到其预期的目的。

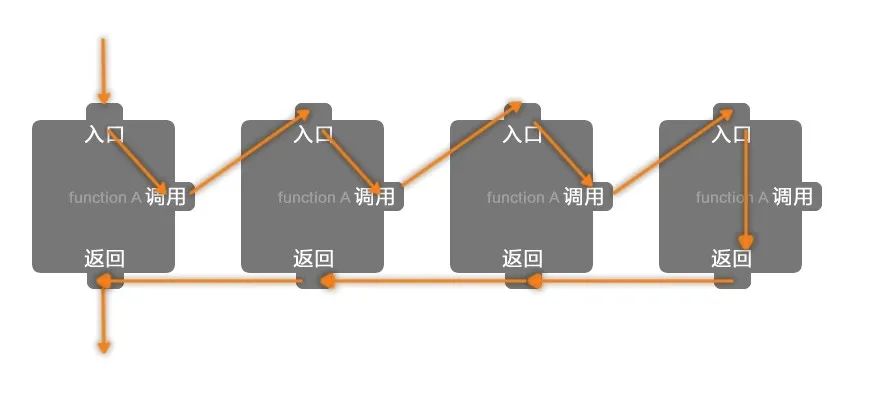
总之，递归是一种强大的技术，可以在许多不同的应用程序中使用。

它可以帮助我们解决复杂的问题，并使代码更加简洁和易于理解。

需要注意的是，当n很大时，递归调用可能会导致栈溢出错误。

好了，我们今天就学到这里吧！

如果遇到什么问题，咱们多多交流，共同解决。

我是猫妹，咱们下次见！