1D Party

题解

我们可以将原来的序列随时间变化转化成一个图像，纵轴代表时间，横轴代表 $A$ 的值。

那么我们可以得到这样一个图像：

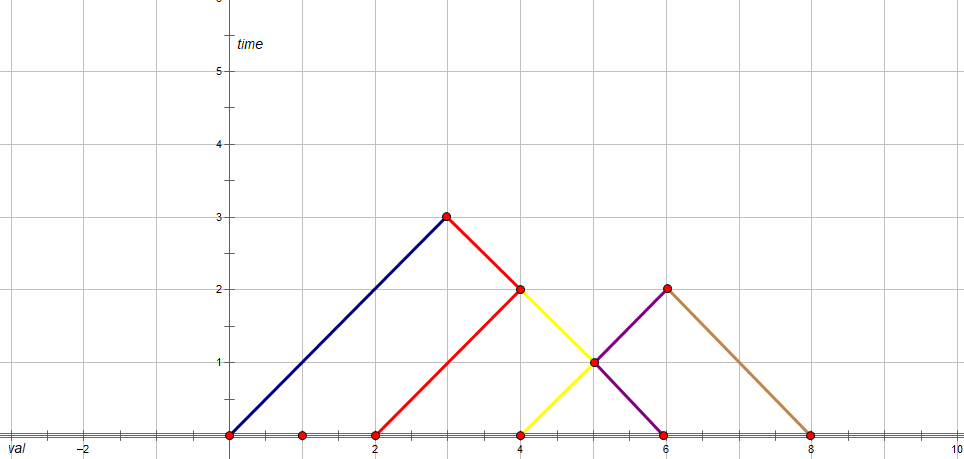
其中不同颜色代表不同的点的运动路径。

由于要最优，我们肯定要让每个点都一直处于运动状态，我们发现每个点大概有一下两种运动状态：

先向左走直到与另一个点相遇，再一直向右走。
先向右走直到与另一个点相遇，再一直向左走。

无论如何，与别的点相遇时都一定会产生一个交点，然后拐弯。

我们可以考虑每个点都不拐弯，而是交换它们的目标对象，也就是 $i$ 与 $i + 1$ 第一次相遇后就让 $i$ 去与 $i + 2$ 相遇， $i + 1$ 与 $i - 1$ 去相遇。

这样我们的图像可以被转化成这个样子：

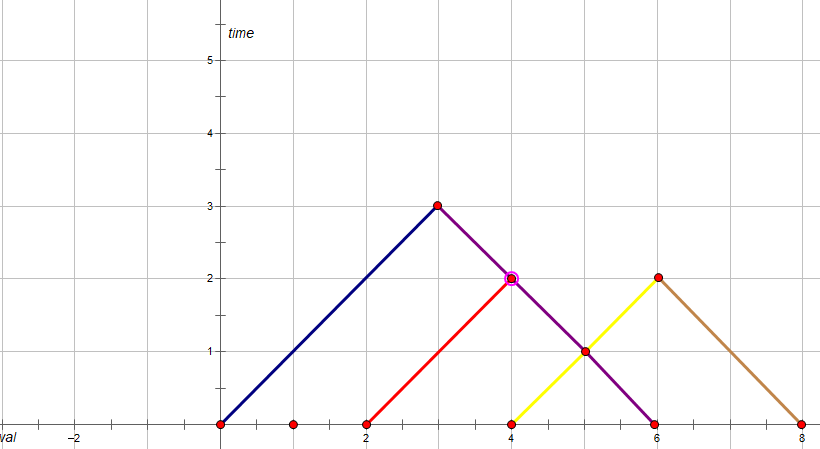
我们相当于得到了无数个三角形连接而成的连通块，当这些三角形所有三角形都联通的时候所有点都是满足条件的。

而我们的答案相当于最高的三角形的最高的高度。

于是我们就很容易想到通过 $d p$ 去找到这个值，设 $dp_{i}$ 表示前 $i$ 个都满足条件的最小高度。

容易得到转移方程式：
$dp_{i}=\min_{j=1}^{i-2}(max(dp_{j},\frac{a_{i}-a_{j-1}}{2}))$
但很明显，如果我们将 $j$ 到 $i - 2$ 都枚举一遍的话时间复杂度就是 $O(n^2)$ 了。但仔细想想，我们真的需要全部都枚举吗？

对于这样一个图形，

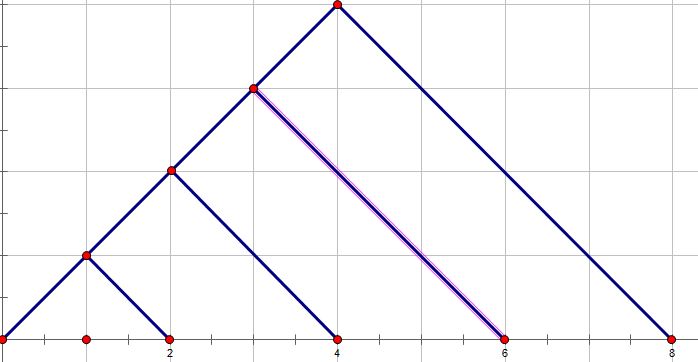
它明显可以被拆分作几个更小的三角形，

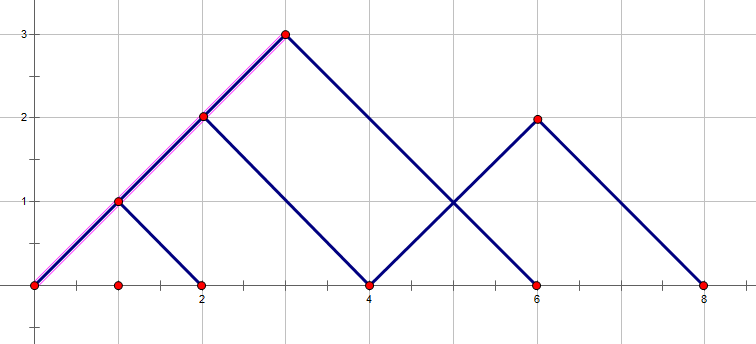
这样经过拆分后明显是可以使值变得更小的。

于是我们对于 $dp_{i}$ 的转移其实是只需要枚举 $dp_{i-2}$ (代表包含 $4$ 个点的三角形)与 $dp_{i-3}$ (代表包含 $5$ 个点的三角形)的。

为什么要枚举 $dp_{i-2}$ 呢，它不是也可以被拆分成两个包含 $4$ 个点的三角形吗？

但很明显如果所有三角形都是 $3$ 个点的就不具有可传递性了，两个三角形或许可以套在一起，但当它们套在一起后就不能继续往下套了，后一个 $3$ 三角形都已经有线段引出了，不可能继续向下套上去。

只有 $4$ 个点的是具有可传递性的：

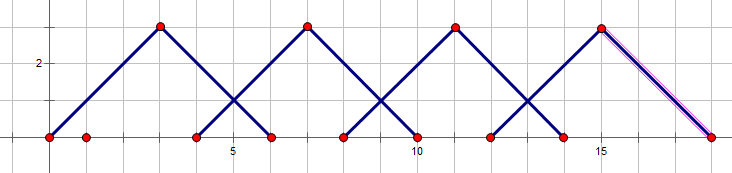
首尾可以是 $3$ 个点的三角形，但由于会影响到是 $a_{4}-a_{1}$ 还是 $a_{5}-a_{2}$ 之类的，还是要都枚举一下，不如说通过特判来得到。

这样也可以说明我们为什么要枚举 $dp_{i-3}$ 了，一个包含 $5$ 个点的三角形，同样会影响到 $4$ 个点的三角形的枚举。

对于这样的情况，

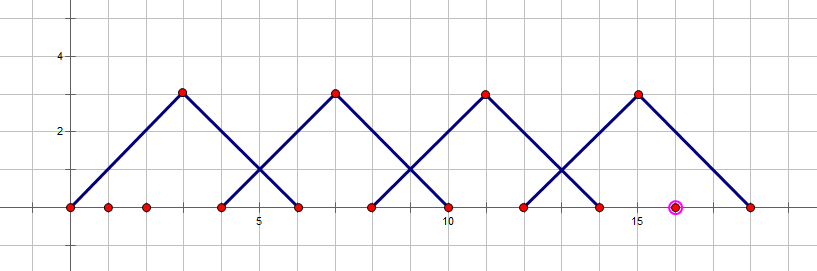
我们枚举 $dp_{i-3}$ 后可能变成这样的情况，

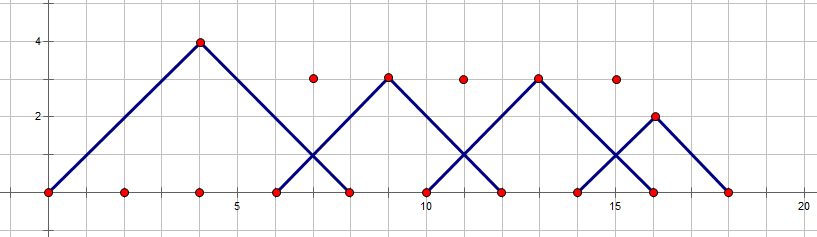
此时原本的 $a_{6}-a_{3}$ 并没有被枚举，取而代之的是 $a_{5}-a_{1}$ 与 $a_{7}-a_{4}$ 。很明显，这样的答案时不一样的，所以我们需要针对这种情况单独枚举。

但如果枚举 $dp_{i-4}$ 就完全没有意义了，

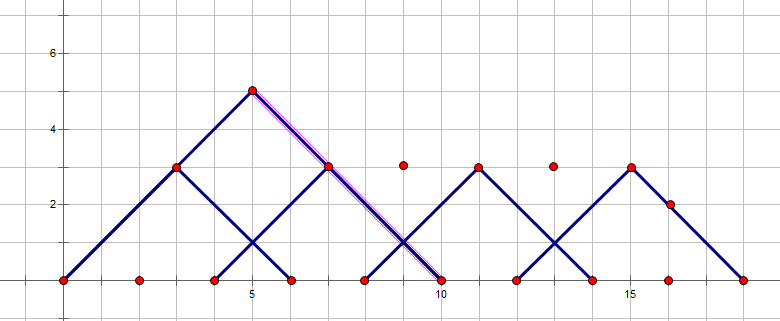
这种情况是完全包含了的，比 $6$ 个点还大的同理也可以被拆分成更小的三角形，所以只需要枚举 $dp_{i-2}$ 与 $dp_{i-3}$ 。

只与枚举最前面和最后面的 $3$ 个点的三角形，我们可以通过建虚点的方式来将其转化成 $4$ 个点的三角形来解决。

时间复杂度 $O\left(n\right)$ 。

还有一种稍劣点的二分做法，就是去二分碰面的时间，再去进行 $d p$ ，这种 $d p$ 就不需要想我们这样考虑这么多了，但它的时间复杂度是 $O\left(nlog\,n\right)$ 。

源码

$O\left(n\right)dp$ 。

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
#define lowbit(x) (x&-x)
#define reg register
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
const int INF=0x7f7f7f7f;
const int mo=998244353;
const int zero=500;
const LL jzm=2333;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
typedef pair<int,int> pii;
const double PI=acos(-1.0);
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int add(int x,int y){return x+y<mo?x+y:x+y-mo;}
int n,a[MAXN],dp[MAXN];
signed main(){read(n);for(int i=1;i<=n;i++)read(a[i]),dp[i]=INF;dp[n+1]=INF;dp[0]=dp[1]=0;dp[2]=a[2]-a[1];a[0]=a[1];a[n+1]=a[n];for(int i=3;i<=n+1;i++)for(int j=i-2;j>=max(1,i-3);j--)dp[i]=min(dp[i],max(dp[j],a[i]-a[j-1]));printf("%d\n",dp[n+1]/2);return 0;
}