本发明涉及三维激光雷达深度数据校正技术领域,具体涉及一种三维固态面阵激光雷达非均匀校正方法。
背景技术:
由于制造工艺限制,三维固态面阵激光雷达中探测器不同像素表现出不同响应特性,同时三维固态面阵激光雷达在长时间工作后,由于温度变化、电路干扰等因素影响,使三维固态面阵激光雷达深度数据发生非均匀性漂移。
目前,国内外已经提出了许多非均匀校正算法,总的来说可以分为两类:一类是基于标定的方法,这种方法具有较高的校正精度,但校正系统体积较大,成本也较高,并且在标定过程中成像系统必须暂停工作,严重制约了该类算法的使用范围。另一类是基于场景的方法,如卡尔曼滤波法、粒子滤波方法等,卡尔曼滤波法在设计时状态空间模型必须为线性和高斯的,而实际非均匀校正过程中这一条件很难达到,另外粒子滤波方法在设计时方差采用固定值或者仅通过场景的变化量近似计算,预测误差较大且粒子分布收敛速度较慢,影响校正实时性。
因此目前需要解决在对三维固态面阵激光雷达进行非均匀性校正时的非线性噪声估计和处理速度慢的问题。
技术实现要素:
有鉴于此,本发明提供了一种三维固态面阵激光雷达非均匀校正方法,能够很好地解决非均匀校正过程中非线性噪声估计和处理速度慢的问题,且准确度高、实时性高、计算量小。
本发明的技术方案为:
一种三维固态面阵激光雷达非均匀校正方法,包括如下步骤:
步骤一、采用三维固态面阵激光雷达采集获得距离图像序列,将采集到的距离图像序列沿时间轴分为K个帧块。
步骤二、根据先验知识确定非均匀性噪声满足的分布函数并进行N次粒子随机采样,每个粒子的初始权值为1/N。
步骤三、利用状态转移模型估计每个粒子的新状态,使粒子都能够按照对应的方式进行状态转移。
状态转移模型为Bk=f(Bk-1)+Wk-1。
其中Bk为第k个帧块中的非均匀性噪声,Wk-1为第k个帧块中的驱动噪声;f(·)为非线性函数。
步骤四、更新第k个帧块中第i个粒子的权值为:
其中δk(n)为第k个帧块中相邻两帧图像,即第n+1帧图像和第n帧图像之间的差值;为δk(n)的均值;其中Yk(1)为第k个帧块中第1帧图像的实际测得的激光信号,对于第k-1个帧块,最后一幅图像Yk-1(lk-1)的校正结果为为第i个粒子的非均匀性噪声分量;δk(n)满足正态分布,σ为标准差;并对所有粒子的权值进行归一化处理。
步骤五、对粒子权重设定一个衡量标准Neff,将权值小于阈值的粒子,依据权值大于Neff的粒子位置进行重新分配。
步骤六、非均匀性噪声噪声为:
根据非均匀性噪声,通过观测模型Yk(n)=Xk(n)+Bk对三维固态面阵激光雷达进行实时校正。
进一步地,步骤四包括如下具体步骤:
S401、同一帧块中相邻两帧图像,即第n+1帧图像和第n帧图像之间的差值为:
δk(n)=Yk(n+1)-Yk(n)=Xk(n+1)-Xk(n)
其中第k个帧块中共lk帧图像,n=1~lk;δk(n)满足正态分布;Yk(n)为实际测得的激光信号;Xk(n)为真实激光信号;
δk(n)的均值为:
S402、Yk(n)和Xk(n)满足:
Yk~N(Xk,σ2),Xk=Yk-Bk
Yk和Xk分别指代Yk(n)和Xk(n)。
S403、最大似然估计值为:
其中Y1:k指代Y1~Yk,X1:k指代X1~Xk。
S404、针对l(σ|Y1:K,X1:K)求σ2的偏导数,并使偏导数为0可得:
S405、对于线性系统,t时刻的σ2表示为t+1时刻的σ2表示为与的递推关系如下,
S406、对于第k-1个帧块,最后一幅图像Yk-1(lk-1)的校正结果为构造变量δk,使得:
则针对第i个粒子的变量为:
δk(n)满足正态分布
S407、则各个粒子的权值为:
进一步地,衡量标准为:
有益效果:
本发明公开的一种基于递推最大似然估计的方法,一方面可以很好地解决非均匀校正过程中非线性噪声估计和处理速度慢的问题,另一方面使粒子分布快速收敛到像素输出的真实值,即使在选用的粒子数较少的情况下也能保证粒子估计与真实值接近,提高了非均匀性校正的准确性,且减少了计算量。本方法采用递推的计算方式,根据时间序列实时的计算像素输出,具备较高的实时性,非常适合用于实时处理。
附图说明
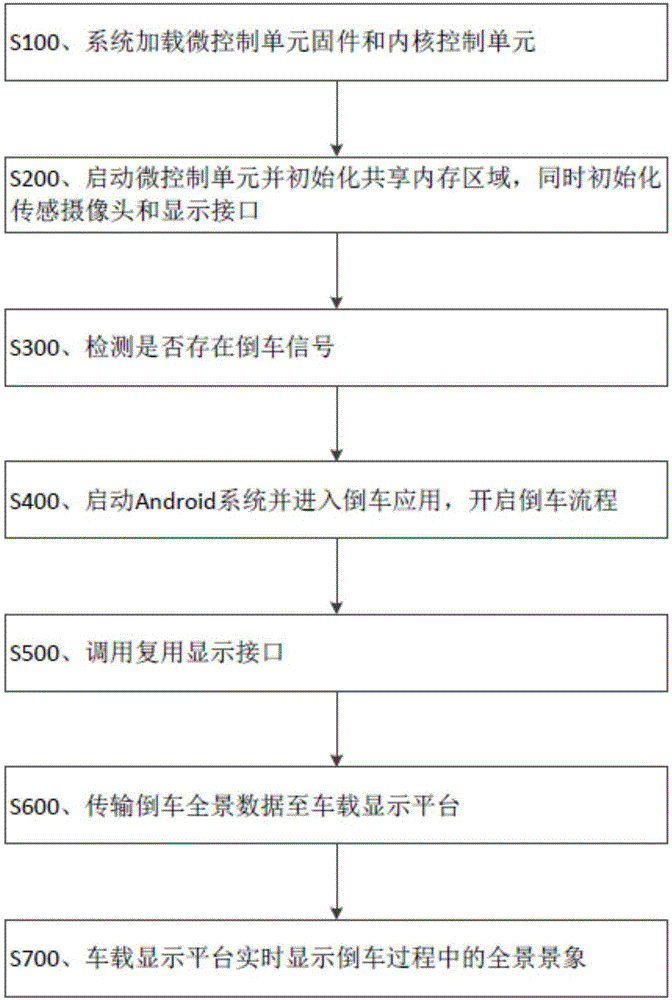
图1为本发明实施例所提供的一种三维固态面阵激光雷达非均匀性校正方法。
具体实施方式
下面结合附图并举实施例,对本发明进行详细描述。
本发明提供了一种三维固态面阵激光雷达非均匀性校正方法,其流程如图1所示,包括如下步骤:
步骤一、采用三维固态面阵激光雷达采集获得距离图像序列,将采集到的距离图像序列沿时间轴分为K个帧块;
步骤二、根据先验知识确定非均匀性噪声满足的分布函数并进行N次粒子随机采样,每个粒子的初始权值为1/N;
步骤三、利用状态转移模型估计每个粒子的新状态,使粒子都能够按照对应的方式进行状态转移;
状态转移模型为Bk=f(Bk-1)+Wk-1;
其中Bk为第k个帧块中的非均匀性噪声,Wk-1为第k个帧块中的驱动噪声;f(·)为非线性函数;
步骤四、根据时间序列采用最大似然估计方法进行方差的计算,进一步更新第k个帧块中第i个粒子的权值为:
其中δk(n)为第k个帧块中相邻两帧图像,即第n+1帧图像和第n帧图像之间的差值;为δk(n)的均值;其中Yk(1)为第k个帧块中第1帧图像的实际测得的激光信号,对于第k-1个帧块,最后一幅图像Yk-1(lk-1)的校正结果为为第i个粒子的非均匀性噪声分量;δk(n)满足正态分布,σ为标准差;并对所有粒子的权值进行归一化处理。
本发明实施例中,采用如下具体步骤求粒子的权值:
S401、同一帧块中相邻两帧图像,即第n+1帧图像和第n帧图像之间的差值为:
δk(n)=Yk(n+1)-Yk(n)=Xk(n+1)-Xk(n)
其中第k个帧块中共lk帧图像,n=1~lk;δk(n)满足正态分布;Yk(n)为实际测得的激光信号;Xk(n)为真实激光信号;
δk(n)的均值为:
S402、Yk(n)和Xk(n)满足:
Yk~N(Xk,σ2),Xk=Yk-Bk
Yk和Xk分别指代Yk(n)和Xk(n)。
S403、最大似然估计值为:
其中Y1:k指代Y1~Yk,X1:k指代X1~Xk。
S404、针对l(σ|Y1:K,X1:K)求σ2的偏导数,并使偏导数为0可得:
S405、对于线性系统,t时刻的σ2表示为t+1时刻的σ2表示为与的递推关系如下,
S406、对于第k-1个帧块,最后一幅图像Yk-1(lk-1)的校正结果为构造变量δk,使得:
则针对第i个粒子的变量为:
δk(n)满足正态分布
S407、则各个粒子的权值为:
步骤五、对粒子权重设定一个衡量标准Neff,将权值小于阈值的粒子,依据权值大于Neff的粒子位置进行重新分配。
本发明实施例中,衡量标准设定为:
步骤六、非均匀性噪声噪声为:
根据非均匀性噪声,通过观测模型Yk(n)=Xk(n)+Bk对三维固态面阵激光雷达进行实时校正。
本发明公开的一种基于递推最大似然估计的方法,一方面可以很好地解决非均匀校正过程中非线性噪声估计和处理速度慢的问题,另一方面使粒子分布快速收敛到像素输出的真实值,即使在选用的粒子数较少的情况下也能保证粒子估计与真实值接近,提高了非均匀性校正的准确性,且减少了计算量。本方法采用递推的计算方式,根据时间序列实时的计算像素输出,具备较高的实时性,非常适合用于实时处理。
综上所述,以上仅为本发明的较佳实施例而已,并非用于限定本发明的保护范围。凡在本发明的精神和原则之内,所作的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。