860.柠檬水找零

力扣题目链接

文章讲解：860.柠檬水找零

视频讲解：贪心算法，看上去复杂，其实逻辑都是固定的！LeetCode：860.柠檬水找零

状态：这个题还是比较简单的，重点就是思路

贪心+模拟解题。

局部最优：遇到账单20，优先消耗美元10，完成本次找零。

全局最优：完成全部账单的找零。

伪代码实现

• 首先我们手里一分钱都没有：

  int five = 0, ten = 0, twenty = 0;
  

• 遇到5美元顾客

if (bill == 5) five++;

• 遇到10美元顾客

if (bill == 10){if (five <= 0) return false;ten++;five--;
}

• 遇到20美元：因为5美元即可以找10美元也可以找20美元，所以我们遇到20美元先用10美元来找零

if (five > 0 && ten > 0){five--;ten--;twenty++;
}else if (five >= 3) {five -= 3;twenty++;
}else return false;

CPP代码

class Solution {
public:bool lemonadeChange(vector<int>& bills) {int five = 0, ten = 0, twenty = 0;for (int bill : bills) {// 情况一if (bill == 5) five++;// 情况二if (bill == 10) {if (five <= 0) return false;ten++;five--;}// 情况三if (bill == 20) {// 优先消耗10美元，因为5美元的找零用处更大，能多留着就多留着if (five > 0 && ten > 0) {five--;ten--;twenty++; // 其实这行代码可以删了，因为记录20已经没有意义了，不会用20来找零} else if (five >= 3) {five -= 3;twenty++; // 同理，这行代码也可以删了} else return false;}}return true;}
};

406.根据身高重建队列

力扣题目链接

文章讲解：406.根据身高重建队列

视频讲解：贪心算法，不要两边一起贪，会顾此失彼 | LeetCode：406.根据身高重建队列

状态：本题我觉得最难的点就是将两个点分开考虑其实也是局部最优的一种，也就是说局部并不是说某个个体的多个方面，也可以是一个方面的全局考虑，然后再考虑其他方面的全局情况，然后构成全局最优。

思路

本题的思路是怎么来的呢？首先这里举个例子，h和k分别表示身高和队列前面身高大于等于该的人数

如果我们考虑k，并且如果k相同就把身高h小的放到队伍后面（因为k相同大身高如果放前面，k值肯定会冲突了）。这样考虑k的情况下：

从图中可以看出，现在顺序还是乱乱得，并且并不好按照一个统一的思想进行调整。

那么我们考虑先按照h排序：

从上图中可以看出，我们的身高这个维度已经固定了，我们再按照k这个维度从前往后遍历去进行排序。

涉及到两个纬度的比较，一定要分别考虑，这样思路才清晰。

综上：

局部最优——首先按身高排序，然后考虑k的插入。

全局最优——最后昨晚插入操作，整个队列满足题目队列属性。

伪代码实现

• 按照身高排序

static bool cmp (const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0]
}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort (people.begin(), people.end(), cmp);
}

• 定义一个二维向量来存放结果，并且就其k值来排序。由于我们已经按照身高排好序了，所以本文中我们只考虑k，并且对于k相同来说，身高小的排前面。

vector<vector<int>> que;
for (int i = 0; i < people.size(); i++){int postition = people[i][1];que.insert(que.begin() + position, people[i]);//暗含k相同情况下身高小的排在前面
}
requrn que;

代码优化

使用vector是非常费时的，C++中vector（可以理解是一个动态数组，底层是普通数组实现的）如果插入元素大于预先普通数组大小，vector底部会有一个扩容的操作，即申请两倍于原先普通数组的大小，然后把数据拷贝到另一个更大的数组上。

所以使用vector（动态数组）来insert，是费时的，插入再拷贝的话，单纯一个插入的操作就是O(n²)了，甚至可能拷贝好几次，就不止O(n²)了。

用链表实现插入操作

list<vector<int>> que;
for (int i = 0; i < people.size(); i++){int position = people[i][1];//插入到下标为position的位置auto it = que.begin();while (position--){it++;}que.insert(it, people[i]);return vector<vector<int>>(que.begin(), que.end());
}

CPP代码

//链表实现
class Solution {
public:// 身高从大到小排（身高相同k小的站前面）static bool cmp(const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort (people.begin(), people.end(), cmp);list<vector<int>> que; // list底层是链表实现，插入效率比vector高的多for (int i = 0; i < people.size(); i++) {int position = people[i][1]; // 插入到下标为position的位置std::list<vector<int>>::iterator it = que.begin();while (position--) { // 寻找在插入位置it++;}que.insert(it, people[i]);}return vector<vector<int>>(que.begin(), que.end());}
};

452. 用最少数量的箭引爆气球

力扣题目链接
文章讲解452. 用最少数量的箭引爆气球
视频讲解：贪心算法，判断重叠区间问题 | LeetCode：452.用最少数量的箭引爆气球
状态：重叠问题是贪心算法中很重要的一类问题，一定要拿下！

思路

先将题目可视化一下子：

y轴是未知的，x轴是确定的，表示了气球的大小。对于points:[[1, 2] [3, 6] [7, 12] [4, 8] [10 16]]

输出：3

弓箭垂直于x轴往上射，每一次都尽量射爆最多的气球。

这样很容易可以推导出局部最优和全局最优：

局部最优——让弓箭尽可能射爆重叠的气球；

全局最优——把所有气球引爆，用的弓箭最少。

最真实的模拟过程其实是，每射爆一个气球就remove一个元素，但是我们其实完全可以先将气球排序，从前到后遍历气球，被射过的气球仅仅跳过就行。

伪代码实现

• 对数组进行排序：这是为了让我们更直观的观察到重叠的气球，这里我们按照气球的起始位置开始排序。

static bool cmp(const vector<int>& a, const vector<int>& b) {return a[0] < b[0];
}
int findMinArrowShots(vector<vector<int>>& points) {if (points.size() == 0) return 0;sort(points.begin(), points.end(), cmp);
};

• 在遍历过程中如果遇到重叠气球，就找到所有重叠气球中有边界的最小值，来上一根弓箭。
  • 以题目示例： [[10,16],[2,8],[1,6],[7,12]]为例，如图：（方便起见，已经排序）
  • 代码实现上面还是非常精妙的，要反复体会
  • 

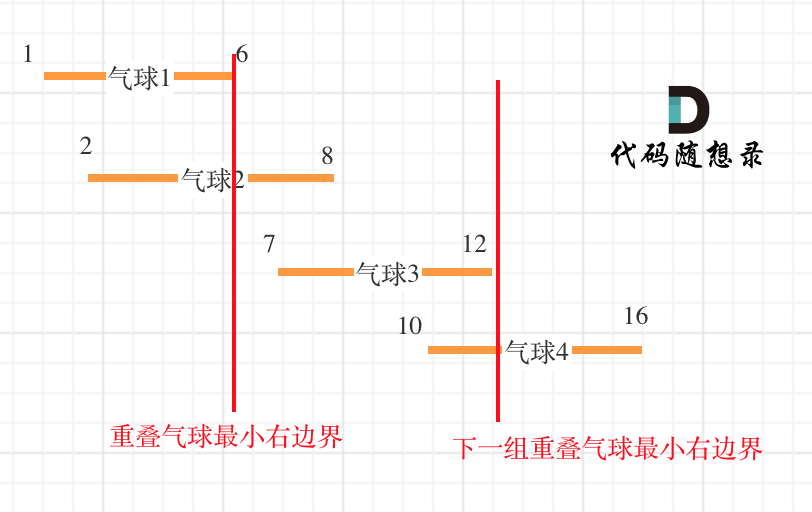
int result = 1; // points 不为空至少需要一支箭for (int i = 1; i < points.size(); i++) {//当前气球的起始位置大于前一个气球的终止位置if (points[i][0] > points[i - 1][1]) {  // 气球i和气球i-1不挨着，注意这里不是>=result++; // 需要一支箭}else {  // 气球i和气球i-1挨着points[i][1] = min(points[i - 1][1], points[i][1]); // 更新重叠气球最小右边界}}return result;

CPP代码

class Solution {
private:static bool cmp(const vector<int>& a, const vector<int>& b) {return a[0] < b[0];}
public:int findMinArrowShots(vector<vector<int>>& points) {if (points.size() == 0) return 0;sort(points.begin(), points.end(), cmp);int result = 1; // points 不为空至少需要一支箭for (int i = 1; i < points.size(); i++) {if (points[i][0] > points[i - 1][1]) {  // 气球i和气球i-1不挨着，注意这里不是>=result++; // 需要一支箭}else {  // 气球i和气球i-1挨着points[i][1] = min(points[i - 1][1], points[i][1]); // 更新重叠气球最小右边界}}return result;}
};
时间复杂度：O(nlog n)，因为有一个快排
空间复杂度：O(1)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间