【C 数据结构】深度优先搜索、广度优先搜索

devtools/2024/9/23 9:26:25/

文章目录

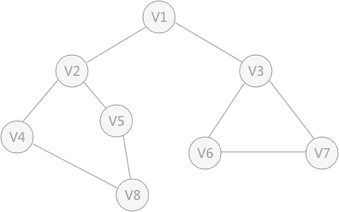
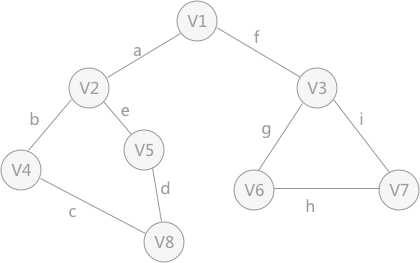
  • 对存储的图中的顶点进行遍历搜索，常用的遍历方式有两种：深度优先搜索和广度优先搜索。

【 1. DFS 深度优先搜索 】

1.1 基本原理

  • 深度优先搜索的过程 类似于树的先序遍历，首先从例子中体会深度优先搜索。例如下图是一个无向图，采用深度优先算法遍历这个图的过程为：
    • 首先任意找一个未被遍历过的顶点，例如从 V1 开始，由于 V1 率先访问过了，所以，需要标记 V1 的状态为访问过；
    • 然后遍历 V1 的邻接点，例如访问 V2 ，并做标记，然后访问 V2 的邻接点，例如 V4 （做标记），然后 V8 ，然后 V5 ；
    • 当继续遍历 V5 的邻接点时，根据之前做的标记显示，所有V5 的邻接点都被访问过了。此时，从 V5 回退到 V8 ，看 V8 是否有未被访问过的邻接点，如果没有，继续回退到 V4 ， V2 ，V1 ；
    • 通过查看 V1 ，找到一个未被访问过的顶点 V3 ，继续遍历，然后访问 V3 邻接点 V6 ，然后 V7 ；
    • 由于 V7 没有未被访问的邻接点，所以回退到 V6 ，继续回退至 V3 ，最后到达 V1 ，发现没有未被访问的；
    • 最后一步需要判断是否所有顶点都被访问，如果还有没被访问的，以未被访问的顶点为第一个顶点，继续依照上边的方式进行遍历。
    • 根据上边的过程，可以得到下图通过深度优先搜索获得的顶点的遍历次序为：
      V1、V2、V4、V8、 V5、V3、V6、V7
      在这里插入图片描述
  • 总结：深度优先搜索，是从图中的一个顶点出发，每次遍历当前访问顶点的临接点，一直到访问的顶点没有未被访问过的临接点为止。然后采用依次回退的方式（深度优先搜索是一个不断回溯的过程），查看来的路上每一个顶点是否有其它未被访问的临接点。访问完成后，判断图中的顶点是否已经全部遍历完成，如果没有，以未访问的顶点为起始点，重复上述过程。

1.2 C 实现

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#define MAX_VERtEX_NUM 20         //顶点的最大个数
#define VertexType int            //顶点的数据类型
#define VRType int                //顶点之间的关系的变量类型
#define InfoType char             //存储弧或边额外信息的指针变量类型
bool visited[MAX_VERtEX_NUM];     //设置全局数组，记录标记顶点是否被访问过//边的信息结构体
typedef struct {VRType adj;         //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。InfoType* info;     //弧或边额外含有的信息指针
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];//图结构体
typedef struct {VertexType vexs[MAX_VERtEX_NUM];   //一维数据数组AdjMatrix  arcs;                   //二维关系数组，即邻接矩阵int vexnum, arcnum;                //图的顶点数和弧（边）数
}MGraph;//根据顶点本身数据，判断出顶点在二维数组中的位置
int LocateVex(MGraph* G, VertexType v) {int i = 0;//遍历一维数组，找到变量vfor (; i < G->vexnum; i++) {if (G->vexs[i] == v) {break;}}//如果找不到，输出提示语句，返回-1if (i > G->vexnum) {printf("no such vertex.\n");return -1;}return i;
}//构造无向图
void CreateDN(MGraph* G) {scanf("%d,%d", &(G->vexnum), &(G->arcnum));for (int i = 0; i < G->vexnum; i++) {scanf("%d", &(G->vexs[i]));}for (int i = 0; i < G->vexnum; i++) {for (int j = 0; j < G->vexnum; j++) {G->arcs[i][j].adj = 0;G->arcs[i][j].info = NULL;}}for (int i = 0; i < G->arcnum; i++) {int v1, v2;scanf("%d,%d", &v1, &v2);int n = LocateVex(G, v1);int m = LocateVex(G, v2);if (m == -1 || n == -1) {printf("no this vertex\n");return;}G->arcs[n][m].adj = 1;G->arcs[m][n].adj = 1;//无向图的二阶矩阵沿主对角线对称}
}//返回第一个与顶点v有边的顶点的下标
int FirstAdjVex(MGraph G, int v)
{//查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标for (int i = 0; i < G.vexnum; i++) {if (G.arcs[v][i].adj) {return i;}}return -1;
}//返回从第w+1个位置开始，与顶点v有边的顶点的下标
int NextAdjVex(MGraph G, int v, int w)
{//从前一个访问位置w的下一个位置开始，查找之间有边的顶点for (int i = w + 1; i < G.vexnum; i++) {if (G.arcs[v][i].adj) {return i;}}return -1;
}//打印输出顶点v的值
void visitVex(MGraph G, int v) {printf("%d ", G.vexs[v]);
}//深度优先搜索核心函数
void DFS(MGraph G, int v) {visited[v] = true;//标记为true，表示这个顶点已被处理visitVex(G, v);   //输出第v个顶点//从该顶点的第一个边开始，一直到最后一个边，对处于边另一端的顶点调用DFS函数for (int w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w)) {//如果该顶点的标记位false，证明未被访问，调用深度优先搜索函数if (!visited[w]){DFS(G, w);}}
}//对图进行深度优先搜索
void DFSTraverse(MGraph G) 
{int v;//初始化为visit标记数组falsefor (v = 0; v < G.vexnum; ++v) {visited[v] = false;}//对于每个标记为false的顶点调用深度优先搜索函数for (v = 0; v < G.vexnum; v++) {//如果该顶点的标记位为false，则调用深度优先搜索函数if (!visited[v]) {DFS(G, v);}}
}int main() {MGraph G; //建立一个图的对象CreateDN(&G);   //初始化图DFSTraverse(G); //深度优先搜索图return 0;
}
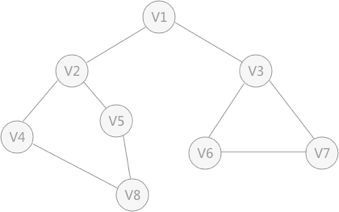
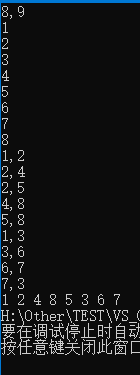
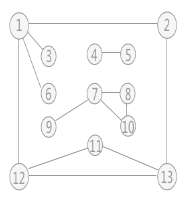
  • 使用上述程序存储下图的无向图时，输入如下数据，得到DFS的输出结果：
    在这里插入图片描述
//输入如下数据：
8,9
1
2
3
4
5
6
7
8
1,2
2,4
2,5
4,8
5,8
1,3
3,6
6,7
7,3

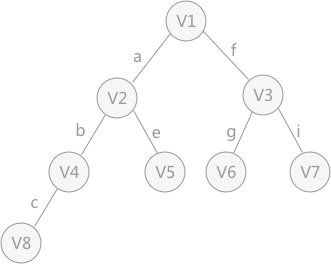
在这里插入图片描述

【 2. BFS 广度优先搜索 】

2.1 基本原理

  • 广度优先搜索 类似于树的层次遍历。以下图的无向图为例，假设 V1 作为起始点，遍历其所有的邻接点 V2 和 V3 ，以 V2 为起始点，访问邻接点 V4 和 V5 ，以 V3 为起始点，访问邻接点 V6 、 V7 ，以 V4 为起始点访问 V8 ，以 V5 为起始点，由于 V5 所有的起始点已经全部被访问，所有直接略过， V6 和 V7 也是如此。
    以 V1 为起始点的遍历过程结束后，判断图中是否还有未被访问的点，由于图 1 中没有了，所以整个图遍历结束。遍历顶点的顺序为：
    V1、 V2、 v3、V4、 V5、 V6、 V7、 V8
    在这里插入图片描述
  • 总结：广度优先搜索，是从图中的某一顶点出发，遍历每一个顶点时，依次遍历其所有的邻接点，然后再从这些邻接点出发，同样依次访问它们的邻接点。按照此过程，直到图中所有被访问过的顶点的邻接点都被访问到。最后还需要做的操作就是查看图中是否存在尚未被访问的顶点，若有，则以该顶点为起始点，重复上述遍历的过程。

2.2 C 实现

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20         //顶点的最大个数
#define VertexType int            //顶点的数据类型
#define VRType int                //顶点之间的关系的变量类型
#define InfoType char             //存储弧或边额外信息的指针变量类型
bool visited[MAX_VERtEX_NUM];     //设置全局数组，记录标记顶点是否被访问过//队列
typedef struct Queue {VertexType data;struct Queue* next;
}Queue;//边的信息结构体
typedef struct {VRType adj;         //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。InfoType* info;     //弧或边额外含有的信息指针
}ArcCell, AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];//图结构体
typedef struct {VertexType vexs[MAX_VERtEX_NUM];   //一维数据数组AdjMatrix  arcs;                   //二维关系数组，即邻接矩阵int vexnum, arcnum;                //图的顶点数和弧（边）数
}MGraph;//根据顶点本身数据，判断出顶点在二维数组中的位置
int LocateVex(MGraph* G, VertexType v) {int i = 0;//遍历一维数组，找到变量vfor (; i < G->vexnum; i++) {if (G->vexs[i] == v) {break;}}//如果找不到，输出提示语句，返回-1if (i > G->vexnum) {printf("no such vertex.\n");return -1;}return i;
}//构造无向图
void CreateDN(MGraph* G) {scanf("%d,%d", &(G->vexnum), &(G->arcnum));for (int i = 0; i < G->vexnum; i++) {scanf("%d", &(G->vexs[i]));}for (int i = 0; i < G->vexnum; i++) {for (int j = 0; j < G->vexnum; j++) {G->arcs[i][j].adj = 0;G->arcs[i][j].info = NULL;}}for (int i = 0; i < G->arcnum; i++) {int v1, v2;scanf("%d,%d", &v1, &v2);int n = LocateVex(G, v1);int m = LocateVex(G, v2);if (m == -1 || n == -1) {printf("no this vertex\n");return;}G->arcs[n][m].adj = 1;G->arcs[m][n].adj = 1;//无向图的二阶矩阵沿主对角线对称}
}//返回第一个与顶点v有边的顶点的下标
int FirstAdjVex(MGraph G, int v)
{//查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标for (int i = 0; i < G.vexnum; i++) {if (G.arcs[v][i].adj) {return i;}}return -1;
}//返回从第w+1个位置开始，与顶点v有边的顶点的下标
int NextAdjVex(MGraph G, int v, int w)
{//从前一个访问位置w的下一个位置开始，查找之间有边的顶点for (int i = w + 1; i < G.vexnum; i++) {if (G.arcs[v][i].adj) {return i;}}return -1;
}//打印输出顶点v的值
void visitVex(MGraph G, int v) {printf("%d ", G.vexs[v]);
}//初始化队列
void InitQueue(Queue** Q) {(*Q) = (Queue*)malloc(sizeof(Queue));(*Q)->next = NULL;
}//顶点元素v进队列
void EnQueue(Queue** Q, VertexType v) {Queue* element = (Queue*)malloc(sizeof(Queue));element->data = v;element->next = NULL;Queue* temp = (*Q);while (temp->next != NULL){temp = temp->next;}temp->next = element;
}//队头元素出队列，队列新的队头元素值赋给u
void DeQueue(Queue** Q, int* u) {(*u) = (*Q)->next->data;(*Q)->next = (*Q)->next->next;
}//判断队列是否为空
bool QueueEmpty(Queue* Q) {if (Q->next == NULL) {return true;}return false;
}
//广度优先搜索
void BFSTraverse(MGraph G) {int v;//将用做标记的visit数组初始化为falsefor (v = 0; v < G.vexnum; ++v) {visited[v] = false;}//对于每个标记为false的顶点调用深度优先搜索函数Queue* Q;  //创建1个队列指针QInitQueue(&Q);for (v = 0; v < G.vexnum; v++) {    // [对每个顶点v循环]if (!visited[v]) {visited[v] = true;      //标记为true，表示这个顶点已被处理visitVex(G,v);          //输出第v个顶点EnQueue(&Q, G.vexs[v]); //将第v个顶点入队while (!QueueEmpty(Q)) {    // [判断队列是否为空]int u;DeQueue(&Q, &u);      //出队，并将新的队头的值赋值给uu = LocateVex(&G, u); //新的队头的值对应的下标for (int w = FirstAdjVex(G,u); w >= 0; w = NextAdjVex(G, u, w)) { //将队头u的所有临接点遍历，并入队if (!visited[w]) {visited[w] = true;visitVex(G, w);EnQueue(&Q, G.vexs[w]);}}}}}
}int main() {MGraph G;      //建立一个图的对象CreateDN(&G);  //初始化图BFSTraverse(G);//广度优先搜索图return 0;
}
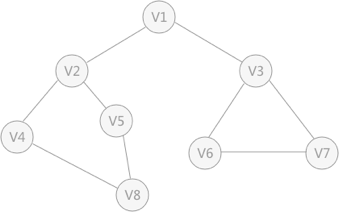
  • 使用上述程序存储下图的无向图时，输入如下数据，得到DFS的输出结果：
    在这里插入图片描述
//输入数据如下：
8,9
1
2
3
4
5
6
7
8
1,2
2,4
2,5
4,8
5,8
1,3
3,6
6,7
7,3

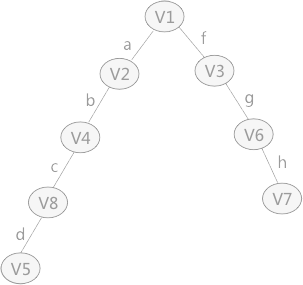
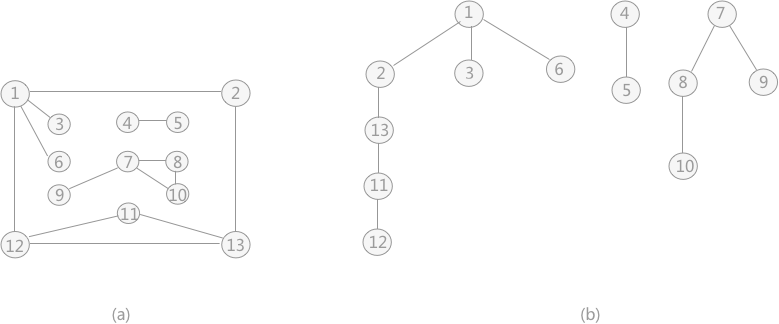
在这里插入图片描述

【 3. 深度优先生成树、广度优先生成树 】

  • 无向图遍历过程中所经历过的图中的顶点和边的组合，就是图的生成树或者生成森林。
    在这里插入图片描述
  • 由深度优先搜索得到的树为 深度优先生成树。例如，当对上图的无向图使用深度优先搜索算法时，假设 V1 作为遍历的起始点，涉及到的顶点和边的遍历顺序为（不唯一）：
    V1、V2、V4、V8、V5、V3、V6、V7。
    此种遍历顺序构建的生成树为：
    在这里插入图片描述
  • 同理，广度优先搜索生成的树为 广度优先生成树，对该无向图以顶点 V1 为起始点进行广度优先搜索遍历得到的树，如下图所示：
    在这里插入图片描述

【 4. 深度优先生成森林、广度优先生成森林 】

  • 前言回顾：详情见：【C 数据结构】图。
    ① 非连通图在进行遍历时，实则是对非连通图中每个连通分量分别进行遍历，在遍历过程经过的每个顶点和边，就构成了每个连通分量的生成树；
    ② 非连通图的多个连通分量构成的多个生成树为非连通图的生成森林。

4.1 深度优先生成森林

  • 对下图 a 的非连通图采用深度优先搜索算法遍历时，得到的深度优先生成森林（由 3 个深度优先生成树构成）如下图 b 所示（不唯一）。

在这里插入图片描述

  • C 实现：
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20         //顶点的最大个数
#define VertexType int            //顶点的数据类型
#define VRType int                //顶点之间的关系的变量类型
bool visited[MAX_VERtEX_NUM];     //设置全局数组，记录标记顶点是否被访问过//边的信息结构体
typedef struct 
{VRType adj;     //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
}ArcCell, AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];//图结构体
typedef struct {VertexType vexs[MAX_VERtEX_NUM];   //一维数据数组AdjMatrix  arcs;                   //二维关系数组，即邻接矩阵int vexnum, arcnum;                //图的顶点数和弧（边）数
}MGraph;//孩子兄弟表示法的链表结点结构
typedef struct CSNode {VertexType data;struct CSNode* lchild;//孩子结点struct CSNode* nextsibling;//兄弟结点
}*CSTree, CSNode;//根据顶点本身数据，判断出顶点在二维数组中的位置
int LocateVex(MGraph G, VertexType v) {int i = 0;//遍历一维数组，找到变量vfor (; i < G.vexnum; i++) {if (G.vexs[i] == v) {break;}}//如果找不到，输出提示语句，返回-1if (i > G.vexnum) {printf("no such vertex.\n");return -1;}return i;
}
//构造无向图
void CreateDN(MGraph* G) {scanf("%d,%d", &(G->vexnum), &(G->arcnum));getchar();for (int i = 0; i < G->vexnum; i++) {scanf("%d", &(G->vexs[i]));}for (int i = 0; i < G->vexnum; i++) {for (int j = 0; j < G->vexnum; j++) {G->arcs[i][j].adj = 0;}}for (int i = 0; i < G->arcnum; i++) {int v1, v2;scanf("%d,%d", &v1, &v2);int n = LocateVex(*G, v1);int m = LocateVex(*G, v2);if (m == -1 || n == -1) {printf("no this vertex\n");return;}G->arcs[n][m].adj = 1;G->arcs[m][n].adj = 1;//无向图的二阶矩阵沿主对角线对称}
}//返回第一个与顶点v有边的顶点的下标
int FirstAdjVex(MGraph G, int v)
{//查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标for (int i = 0; i < G.vexnum; i++) {if (G.arcs[v][i].adj) {return i;}}return -1;
}//返回从第w+1个位置开始，与顶点v有边的顶点的下标
int NextAdjVex(MGraph G, int v, int w)
{//从前一个访问位置w的下一个位置开始，查找之间有边的顶点for (int i = w + 1; i < G.vexnum; i++) {if (G.arcs[v][i].adj) {return i;}}return -1;
}void DFSTree(MGraph G, int v, CSTree* T) {//将正在访问的该顶点的标志位设为truevisited[v] = true;bool first = true;CSTree q   = NULL;//依次遍历该顶点的所有邻接点for (int w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w)) {//如果该临界点标志位为false，说明还未访问if (!visited[w]) {//为该邻接点初始化为结点CSTree p = (CSTree)malloc(sizeof(CSNode));p->data = G.vexs[w];p->lchild = NULL;p->nextsibling = NULL;//该结点的第一个邻接点作为孩子结点，其它邻接点作为孩子结点的兄弟结点if (first) {(*T)->lchild = p;first = false;}//否则，为兄弟结点else {q->nextsibling = p;}q = p;//以当前访问的顶点为树根，继续访问其邻接点DFSTree(G, w, &q);}}
}//深度优先搜索生成森林并转化为二叉树
void DFSForest(MGraph G, CSTree* T) {(*T) = NULL;//每个顶点的标记为初始化为falsefor (int v = 0; v < G.vexnum; v++) {visited[v] = false;}CSTree q = NULL;//遍历每个顶点作为初始点，建立深度优先生成树for (int v = 0; v < G.vexnum; v++) {//如果该顶点的标记位为false，证明未访问过if (!(visited[v])) {//新建一个结点，表示该顶点CSTree p = (CSTree)malloc(sizeof(CSNode));p->data = G.vexs[v];p->lchild = NULL;p->nextsibling = NULL;//如果树未空，则该顶点作为树的树根if (!(*T)) {(*T) = p;}//该顶点作为树根的兄弟结点else {q->nextsibling = p;}//每次都要把q指针指向新的结点，为下次添加结点做铺垫q = p;//以该结点为起始点，构建深度优先生成树DFSTree(G, v, &p);}}
}//前序遍历二叉树
void PreOrderTraverse(CSTree T) {if (T) {printf("%d ", T->data);PreOrderTraverse(T->lchild);PreOrderTraverse(T->nextsibling);}return;
}int main() {MGraph G;    //建立一个图的对象CreateDN(&G);//初始化图CSTree T;DFSForest(G, &T);PreOrderTraverse(T);return 0;
}
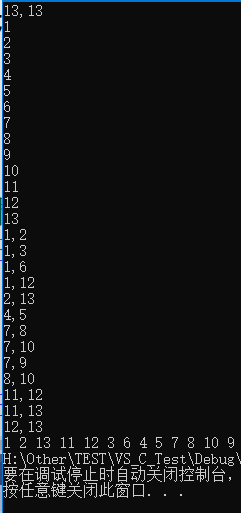
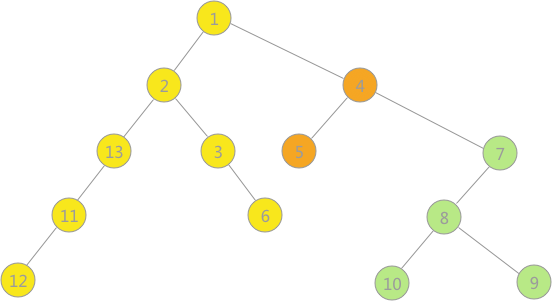
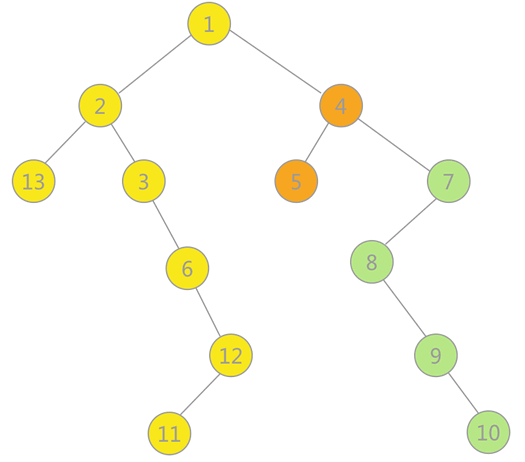
  • 使用上述程序存储下图的无向图，输入如下数据，构建深度优先生成森林，得到DFS的输出结果：
    在这里插入图片描述
  • 构建的深度优先生成森林用孩子兄弟表示法如下所示：3 种颜色的树各代表一棵深度优先生成树，使用孩子兄弟表示法表示，也就是将三棵树的树根相连，第一棵树的树根作为整棵树的树根。
    在这里插入图片描述
//输入数据如下所示：
13,13
1
2
3
4
5
6
7
8
9
10
11
12
13
1,2
1,3
1,6
1,12
2,13
4,5
7,8
7,10
7,9
8,10
11,12
11,13
12,13

在这里插入图片描述

4.2 广度优先生成森林

  • 非连通图采用广度优先搜索算法进行遍历时，经过的顶点以及边的集合为该图的 广度优先生成森林 。
  • C 实现：
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20                   //顶点的最大个数
#define VRType int                          //表示顶点之间的关系的变量类型
#define InfoType char                       //存储弧或者边额外信息的指针变量类型
#define VertexType int                      //图中顶点的数据类型
typedef enum{false,true}bool;               //定义bool型常量
bool visited[MAX_VERtEX_NUM];               //设置全局数组，记录标记顶点是否被访问过
typedef struct {VRType adj;                             //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。InfoType * info;                        //弧或边额外含有的信息指针
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];typedef struct {VertexType vexs[MAX_VERtEX_NUM];        //存储图中顶点数据AdjMatrix arcs;                         //二维数组，记录顶点之间的关系int vexnum,arcnum;                      //记录图的顶点数和弧（边）数
}MGraph;typedef struct CSNode{VertexType data;struct CSNode * lchild;//孩子结点struct CSNode * nextsibling;//兄弟结点
}*CSTree,CSNode;typedef struct Queue{CSTree data;//队列中存放的为树结点struct Queue * next;
}Queue;//根据顶点本身数据，判断出顶点在二维数组中的位置
int LocateVex(MGraph * G,VertexType v){int i=0;//遍历一维数组，找到变量vfor (; i<G->vexnum; i++) {if (G->vexs[i]==v) {break;}}//如果找不到，输出提示语句，返回-1if (i>G->vexnum) {printf("no such vertex.\n");return -1;}return i;
}
//构造无向图
void CreateDN(MGraph *G){scanf("%d,%d",&(G->vexnum),&(G->arcnum));for (int i=0; i<G->vexnum; i++) {scanf("%d",&(G->vexs[i]));}for (int i=0; i<G->vexnum; i++) {for (int j=0; j<G->vexnum; j++) {G->arcs[i][j].adj=0;G->arcs[i][j].info=NULL;}}for (int i=0; i<G->arcnum; i++) {int v1,v2;scanf("%d,%d",&v1,&v2);int n=LocateVex(G, v1);int m=LocateVex(G, v2);if (m==-1 ||n==-1) {printf("no this vertex\n");return;}G->arcs[n][m].adj=1;G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称}
}int FirstAdjVex(MGraph G,int v)
{//查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标for(int i = 0; i<G.vexnum; i++){if( G.arcs[v][i].adj ){return i;}}return -1;
}
int NextAdjVex(MGraph G,int v,int w)
{//从前一个访问位置w的下一个位置开始，查找之间有边的顶点for(int i = w+1; i<G.vexnum; i++){if(G.arcs[v][i].adj){return i;}}return -1;
}//初始化队列
void InitQueue(Queue ** Q){(*Q)=(Queue*)malloc(sizeof(Queue));(*Q)->next=NULL;
}
//结点v进队列
void EnQueue(Queue **Q,CSTree T){Queue * element=(Queue*)malloc(sizeof(Queue));element->data=T;element->next=NULL;Queue * temp=(*Q);while (temp->next!=NULL) {temp=temp->next;}temp->next=element;
}
//队头元素出队列
void DeQueue(Queue **Q,CSTree *u){(*u)=(*Q)->next->data;(*Q)->next=(*Q)->next->next;
}
//判断队列是否为空
bool QueueEmpty(Queue *Q){if (Q->next==NULL) {return true;}return false;
}void BFSTree(MGraph G,int v,CSTree*T){CSTree q=NULL;Queue * Q;InitQueue(&Q);//根结点入队EnQueue(&Q, (*T));//当队列为空时，证明遍历完成while (!QueueEmpty(Q)) {bool first=true;//队列首个结点出队DeQueue(&Q,&q);//判断结点中的数据在数组中的具体位置int v=LocateVex(&G,q->data);//已经访问过的更改其标志位visited[v]=true;//遍历以出队结点为起始点的所有邻接点for (int w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v, w)) {//标志位为false，证明未遍历过if (!visited[w]) {//新建一个结点 p，存放当前遍历的顶点CSTree p=(CSTree)malloc(sizeof(CSNode));p->data=G.vexs[w];p->lchild=NULL;p->nextsibling=NULL;//当前结点入队EnQueue(&Q, p);//更改标志位visited[w]=true;//如果是出队顶点的第一个邻接点，设置p结点为其左孩子if (first) {q->lchild=p;first=false;}//否则设置其为兄弟结点else{q->nextsibling=p;}q=p;}}}
}
//广度优先搜索生成森林并转化为二叉树
void BFSForest(MGraph G,CSTree *T){(*T)=NULL;//每个顶点的标记为初始化为falsefor (int v=0; v<G.vexnum; v++) {visited[v]=false;}CSTree q=NULL;//遍历图中所有的顶点for (int v=0; v<G.vexnum; v++) {//如果该顶点的标记位为false，证明未访问过if (!(visited[v])) {//新建一个结点，表示该顶点CSTree p=(CSTree)malloc(sizeof(CSNode));p->data=G.vexs[v];p->lchild=NULL;p->nextsibling=NULL;//如果树未空，则该顶点作为树的树根if (!(*T)) {(*T)=p;}//该顶点作为树根的兄弟结点else{q->nextsibling=p;}//每次都要把q指针指向新的结点，为下次添加结点做铺垫q=p;//以该结点为起始点，构建广度优先生成树BFSTree(G,v,&p);}}
}
//前序遍历二叉树
void PreOrderTraverse(CSTree T){if (T) {printf("%d ",T->data);PreOrderTraverse(T->lchild);PreOrderTraverse(T->nextsibling);}return;
}
int main() {MGraph G;//建立一个图的变量CreateDN(&G);//初始化图CSTree T;BFSForest(G, &T);PreOrderTraverse(T);return 0;
}
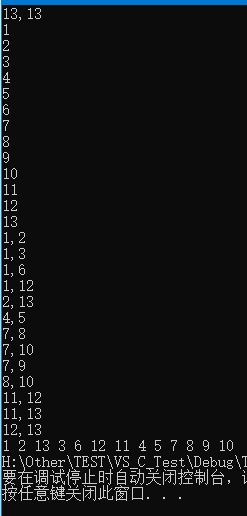
  • 使用上述程序存储下图的无向图，输入如下数据，构建广度优先生成森林，得到BFS的输出结果：
    在这里插入图片描述
//输入如下数据：
13,13
1
2
3
4
5
6
7
8
9
10
11
12
13
1,2
1,3
1,6
1,12
2,13
4,5
7,8
7,10
7,9
8,10
11,12
11,13
12,13

在这里插入图片描述


http://www.ppmy.cn/devtools/30779.html

相关文章

【Leetcode】63- 不同路径II

【Leetcode】63- 不同路径II

问题简述 一个机器人位于一个 m x n 网格的左上角 。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径&#xff1f; 网格中的障碍物和空位置分别用 1 和 0 来表示。 示例 1&#xff1…
阅读更多...
Java | Leetcode Java题解之第63题不同路径II

Java | Leetcode Java题解之第63题不同路径II

题目&#xff1a; 题解&#xff1a; class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int n obstacleGrid.length, m obstacleGrid[0].length;int[] f new int[m];f[0] obstacleGrid[0][0] 0 ? 1 : 0;for (int i 0; i < n; i) {for (i…
阅读更多...
基于Spring Boot的医疗服务系统设计与实现

基于Spring Boot的医疗服务系统设计与实现

基于Spring Boot的医疗服务系统设计与实现 开发语言&#xff1a;Java框架&#xff1a;springbootJDK版本&#xff1a;JDK1.8数据库工具&#xff1a;Navicat11开发软件&#xff1a;eclipse/myeclipse/idea 系统部分展示 医疗服务系统首页界面图&#xff0c;公告信息、医疗地图…
阅读更多...
Ieetcode——21.合并两个有序链表

Ieetcode——21.合并两个有序链表

21. 合并两个有序链表 - 力扣&#xff08;LeetCode&#xff09; 合并两个有序链表我们的思路是创建一个新链表&#xff0c;然后遍历已知的两个有序链表&#xff0c;并比较其节点的val值&#xff0c;将小的尾插到新链表中&#xff0c;然后继续遍历&#xff0c;直到将该两个链表…
阅读更多...
Docker-Compose编排LNMP并部署WordPress

Docker-Compose编排LNMP并部署WordPress

前言 随着云计算和容器化技术的快速发展&#xff0c;使用 Docker Compose 编排 LNMP 环境已经成为快速部署 Web 应用程序的一种流行方式。LNMP 环境由 Linux、Nginx、MySQL 和 PHP 组成&#xff0c;为运行 Web 应用提供了稳定的基础。本文将介绍如何通过 Docker Compose 编排 …
阅读更多...
Linux|awk 特殊模式“BEGIN 和 END”

Linux|awk 特殊模式“BEGIN 和 END”

引言 在本文[1]&#xff0c;我们将介绍Awk的更多特性&#xff0c;特别是两个特殊的模式&#xff1a;BEGIN和END。 这些独特的功能在我们努力扩展和深入探索构建复杂Awk操作的多种方法时&#xff0c;将大有裨益。 实例 让我们从Awk系列的开篇回顾开始&#xff0c;回想一下&#…
阅读更多...
【研发日记】Matlab/Simulink避坑指南(十一)——Delay周期Bug

【研发日记】Matlab/Simulink避坑指南(十一)——Delay周期Bug

文章目录 前言 背景介绍 问题描述 分析排查 解决方案 总结归纳 前言 见《研发日记&#xff0c;Matlab/Simulink避坑指南(六)——字节分割Bug》 见《研发日记&#xff0c;Matlab/Simulink避坑指南(七)——数据溢出钳位Bug》 见《研发日记&#xff0c;Matlab/Simulink避坑指…
阅读更多...
25计算机考研院校数据分析 | 哈尔滨工业大学

25计算机考研院校数据分析 | 哈尔滨工业大学

哈尔滨工业大学&#xff08;Harbin Institute of Technology&#xff09;&#xff0c;简称哈工大&#xff0c; 校本部位于黑龙江省哈尔滨市&#xff0c;是由工业和信息化部直属的全国重点大学&#xff0c;位列国家“双一流”、“985工程”、“211工程”&#xff0c;九校联盟 、…
阅读更多...
最新文章

Copyright @ 2022~2023