问题简述

一个机器人位于一个 m x n 网格的左上角 。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：
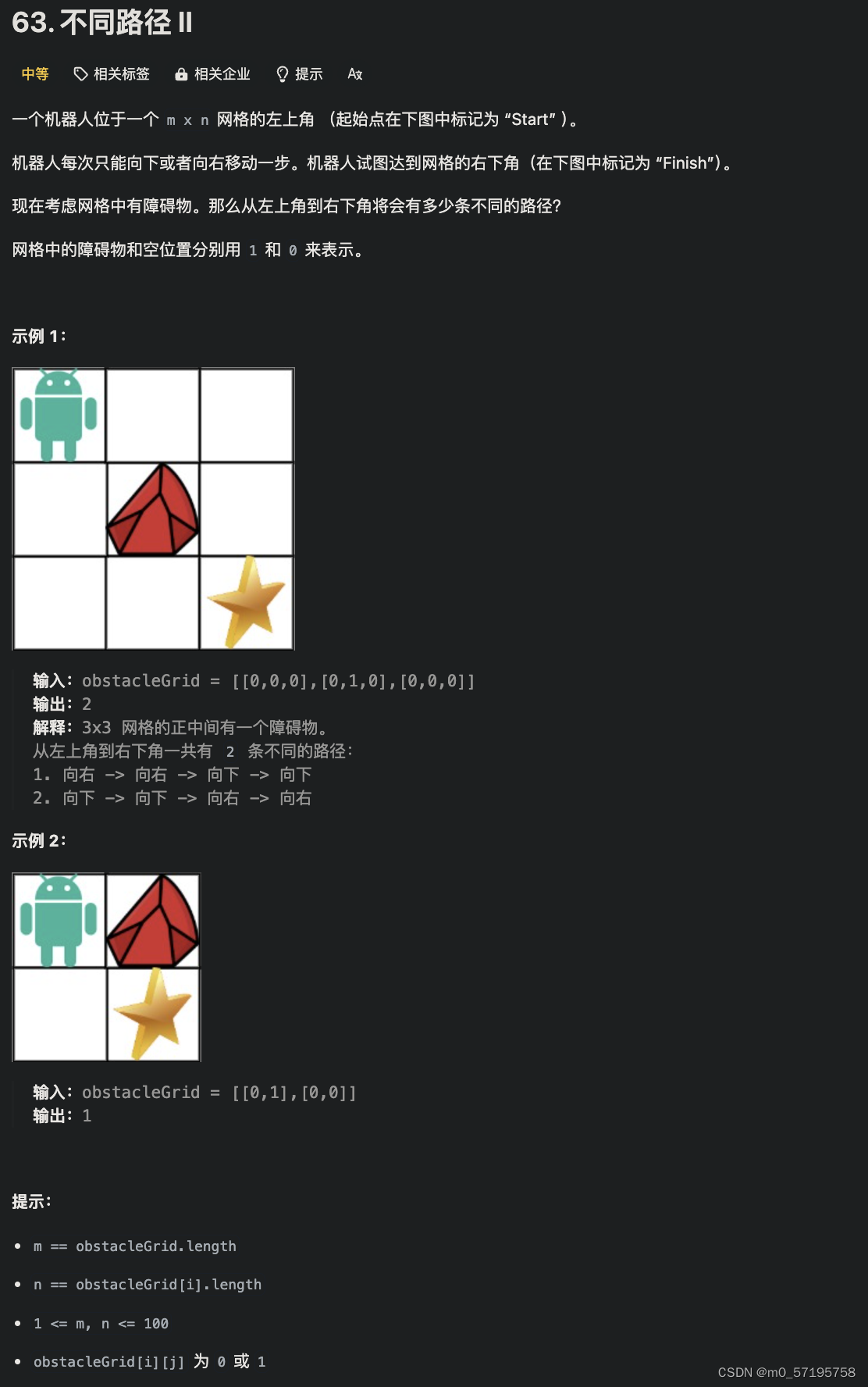
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1、向右 -> 向右 -> 向下 -> 向下
2、向下 -> 向下 -> 向右 -> 向右

示例 2：
输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

思路分析

该题求解也是分阶段的，而且下一阶段的解是基于上一阶段的解（“最优子结构”），但与后面阶段的解无关（“无后效性”）。因此考虑动态规划来求解。将动态的 状态 定义为到达当前位置的路径数。由于只能向右、向下移动，因此每个位置的可到达路径数取决于其左边位置、上边位置的可到达路径数，状态转移方程为：dp[i][j] = dp[i-1][j] + dp[i][j-1]。如果某位置是障碍物，则到达目前位置的可到达路径数应为0，表示不可到达。在一次遍历网格的过程中就可以求得每个位置的可到达路径数，走到网格右下方时即可获得该问题的最终结果。代码实现起来比较简单。

代码示例

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m, n = len(obstacleGrid), len(obstacleGrid[0])"""注意：dp=[[0]*n]*m 这种方式是错误的二维矩阵初始化方式，因为这样其实只会生成1个具有n+1个元素的列表，真实的m行并不存在，而是m个引用指向同一个列表。应该使用列表推导式来初始化一个m*n的二维矩阵。"""dp = [[0 for col in range(n)] for row in range(m)] # 或 dp=[[0]*n for _ in range(m)] # 先判断起点或终点是否有障碍物，若有则直接返回无可达路线的结果。避免进入后续无用的循环计算，大大节省时间开销。if obstacleGrid[0][0] == 1 or obstacleGrid[-1][-1] == 1:return 0for i in range(m):for j in range(n):if obstacleGrid[i][j] == 1: dp[i][j] = 0elif i < 0 and j < 0:dp[i][j] = 1elif i < 0:dp[i][j] = dp[i][j-1]elif j < 0:dp[i][j] = dp[i-1][j]else:dp[i][j] = dp[i][j-1] + dp[i-1][j]return dp[-1][-1]

算法复杂度

由于遍历一次网格需要双层循环，时间复杂度为$O(m\times n)$；
dp数组记录每个网格上的可达路径数量，空间复杂度为$O(m\times n)$。

🌟改进算法——减少空间复杂度

该算法需要遍历整个网格，因此时间复杂度不可降低。但有没有什么办法可以减少空间复杂度呢？
有，使用 【滚动数组】 。动态规划算法中经常用该方法对dp数组进行降维，减少空间复杂度。
当状态转移只与前几个状态有关时，可以使用滚动数组记录这几个状态，而不是记录之前所有的状态。
在本问题中，原本使用m*n大小的二维数组记录每个状态。但由于dp[i][j] = dp[i][j-1] + dp[i-1][j]，状态的转移只与当前位置的上一行（上一行的当前列）、当前行（当前行的左一列）有关，那么我们可以仅用上一行和当前行而不是m行n列去记录之前阶段的状态，另外由于对网格的遍历顺序是从上往下逐行、再在每行中从左往右逐列的，因此实际上只需使用一行状态数组记录网格当前行的最新的状态，就等于为网格当前行的每个位置记录了其 上一行的当前列 和 当前行的左一列 ；如此将空间复杂度由$O(m\times n)$降低至$O(n)$。代码示例如下：

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m, n = len(obstacleGrid), len(obstacleGrid[0])if obstacleGrid[0][0] == 1 or obstacleGrid[-1][-1] == 1:return 0dp = [0] * ndp[0] = 1 if obstacleGrid[0][0] == 0 else 0for i in range(m):for j in range(n):if obstacleGrid[i][j] == 1: dp[j] = 0continueif j-1 >= 0 and obstacleGrid[i][j] == 0:# dp数组记录的是当前行每个位置的最新的状态，遍历到第j个位置时，在更新该位置状态值之前：# dp数组j-1位置的元素记录的是网格中第i行第j-1列的数，dp数组j位置记录的是网格中第i-1行第j列的数。dp[j] += dp[j-1]  return dp[-1]