1 文章信息
文章名为Melding the Data-Decisions Pipeline: Decision-Focused Learning for Combinatorial Optimization 。发表在第33届AAAI Conference on Artificial Intelligence. 作者来自南加州大学。
2 摘要
在现实世界环境中产生影响力需要人工智能技术贯穿从数据到预测模型再到决策的整个流程。这些组件通常被分别处理:首先,通过预测准确性的度量来训练机器学习模型,然后将其预测结果作为输入,输入到产生决策的优化算法中。然而,用于训练模型的损失函数很容易与最终目标(即做出尽可能好的决策)不一致。手动调整损失函数以与优化目标对齐是一个困难且容易出错的过程。
本文专注于组合优化问题,并引入了一个决策聚焦学习的通用框架,在该框架中,机器学习模型与优化算法直接结合进行训练,以产生高质量的决策。从技术上讲,本文的贡献是将常见的离散优化问题类别整合到深度学习或其他预测模型中,这些模型通常通过梯度下降进行训练。主要思想是利用离散问题的连续松弛来在优化过程中传播梯度。本文为两大类组合问题实例化了这个框架:线性规划和子模最大化。在各种领域的实验结果表明,与传统的方法相比,决策聚焦学习通常能带来更优的优化性能。本文发现,标准的准确性度量并不能可靠地反映预测模型在优化中的实用性,而本文方法能够通过将真正目标指定为模型的训练目标,在一系列决策问题中获得显著的回报。
3 简介
在人工智能的许多现实应用中,目标是从数据到预测模型再到决策构建一个流程。这些步骤共同促成了一种基于证据的决策制定形式,这种形式在医疗保健、科学发现、交通运输等众多领域具有变革潜力。这个流程需要两个技术组件:机器学习模型和优化算法。机器学习模型利用数据来预测未知量;优化算法则利用这些预测来做出最大化某个目标的决策。本文关注的是组合优化,它在人工智能的现实应用中无处不在,从为公共住房匹配申请人到选择一组电影进行推荐等。本文聚焦于具有结构化连续松弛的常见组合问题类别,例如线性规划和子模最大化。关于组合优化的文献浩如烟海。然而,重要的是,如果没有更广泛的流程,优化往往是不够的,因为目标函数是未知的,必须通过机器学习进行预测。
尽管近年来机器学习取得了惊人的发展,但典型的训练方法完全将流程的两个部分分开处理。也就是说,系统设计者会首先使用某种标准准确性度量(例如回归问题的均方误差)来训练预测模型。然后,将模型的预测作为输入传递给优化算法以产生决策。这种两阶段方法在许多领域极为常见。当预测模型完美或接近完美时,这种方法是合理的,因为完全准确的预测也会产生最佳决策。然而,在复杂的学习任务中,所有模型都会出错,训练过程隐式地权衡了这些错误将发生的位置。当预测和优化分开时,这种权衡就与更广泛流程的目标(即做出尽可能好的决策)脱节了。
本文提出了一个决策聚焦学习框架,通过将预测和优化集成到一个端到端系统中,从而融合了数据-决策流程。也就是说,预测模型是根据它通过优化算法诱导的决策质量进行训练的。类似的想法最近在凸优化的背景下得到了探索,但据本文所知,本文是首次尝试训练机器学习系统以在组合决策问题上取得性能提升。组合设置带来了新的技术挑战,因为优化问题是离散的。然而,机器学习系统(例如深度神经网络)通常是通过梯度下降进行训练的。
本文的第一个贡献是提出了一个通过解决组合问题性能来训练机器学习模型的通用框架。起点是将组合问题放松为连续问题。然后,本文分析地求解连续问题的最优解作为模型预测的函数。这使本文能够使用离散问题的连续代理进行训练。在测试时,本文将连续解四舍五入到离散点。
本文的第二个贡献是为两大类组合问题实例化这个框架:线性规划和子模最大化问题。线性规划涵盖了许多经典问题,如最短路径、最大流和二分图匹配。反映递减回报直观现象的子模最大化也无处不在;其应用从社交网络到推荐系统等。在每个案例中,本文都解决了一系列技术挑战,以产生可以高效求导的结构化松弛。
最后,本文进行了广泛的实证研究,在一系列领域比较了决策聚焦方法和传统方法。尽管根据标准度量,决策聚焦方法的预测准确性较差,但它们通常能提升整个流程(即决策质量)的性能。直观地看,通过本文的方法训练的预测模型特别关注对做出良好决策至关重要的品质。相比之下,更通用的方法产生的预测中的误差分布方式与底层任务不一致。
4 问题描述
本文考虑形式为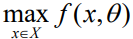 的组合优化问题,其中
的组合优化问题,其中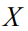 是一个枚举可行决策的离散集合。不失一般性,本文设
是一个枚举可行决策的离散集合。不失一般性,本文设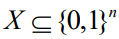 ,决策变量
,决策变量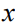 是一个二进制向量。目标函数
是一个二进制向量。目标函数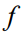 依赖于参数
依赖于参数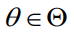 。如果已知,那么可以使用一系列现有技术来解决这个问题。在本文中,本文考虑更具挑战性(但也很普遍)的情况,即
。如果已知,那么可以使用一系列现有技术来解决这个问题。在本文中,本文考虑更具挑战性(但也很普遍)的情况,即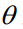 未知,并且必须从数据中推断出来。例如,在二分图匹配问题中,
未知,并且必须从数据中推断出来。例如,在二分图匹配问题中,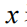 表示每对节点是否匹配,而
表示每对节点是否匹配,而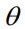 包含匹配每对节点的奖励。在许多应用中,这些亲和度是从历史数据中学习得来的。
包含匹配每对节点的奖励。在许多应用中,这些亲和度是从历史数据中学习得来的。
具体来说,决策者观察到一个与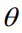 相关的特征向量
相关的特征向量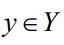 。这引入了一个必须在优化之前解决的学习问题。像经典监督学习一样,本文正式地将
。这引入了一个必须在优化之前解决的学习问题。像经典监督学习一样,本文正式地将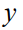 和
和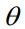 建模为从联合分布
建模为从联合分布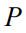 中抽取的。本文的算法将观察从
中抽取的。本文的算法将观察从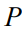 中独立同分布抽取的训练实例
中独立同分布抽取的训练实例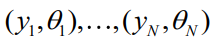 。在测试时,本文会得到一个与未观察到的
。在测试时,本文会得到一个与未观察到的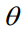 对应的特征向量
对应的特征向量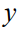 。本文的算法将使用
。本文的算法将使用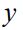 来预测参数值
来预测参数值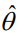 。然后,本文将解决优化问题
。然后,本文将解决优化问题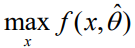 以获得决策
以获得决策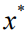 。本文的效用是决策
。本文的效用是决策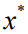 相对于真实但未知的参数
相对于真实但未知的参数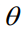 的目标值
的目标值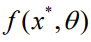 。
。
让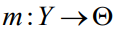 表示一个将观察到的特征映射到参数的模型。本文的目标是(使用训练数据)找到一个模型
表示一个将观察到的特征映射到参数的模型。本文的目标是(使用训练数据)找到一个模型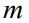 ,该模型可以最大化底层优化任务的预期性能。定义
,该模型可以最大化底层优化任务的预期性能。定义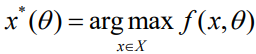 为给定
为给定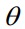 的最优。数据和决策流程的最终目标是最大化
的最优。数据和决策流程的最终目标是最大化
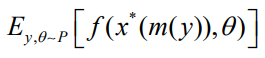
这个问题的经典方法是两阶段方法,它首先使用与任务无关的损失函数(例如均方误差)来学习模型,然后使用学习到的模型来解决优化问题。模型类将有自己的参数化,本文用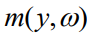 来表示。例如,模型类可能由深度神经网络组成,其中
来表示。例如,模型类可能由深度神经网络组成,其中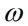 表示权重。两阶段方法首先解决以下问题
表示权重。两阶段方法首先解决以下问题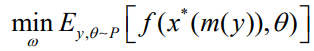 ,其中 L 是一个损失函数。这样的损失函数衡量了模型预测的整体“准确性”,但没有特别考虑当模型用于决策制定时表现如何。本文解决的问题是,是否可以通过专门训练模型以在决策问题上表现良好来做得更好。
,其中 L 是一个损失函数。这样的损失函数衡量了模型预测的整体“准确性”,但没有特别考虑当模型用于决策制定时表现如何。本文解决的问题是,是否可以通过专门训练模型以在决策问题上表现良好来做得更好。
<1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;">1><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;">5 具体实现1>
本文的目标是将组合优化整合到基于梯度的训练循环中。也就是说,本文旨在通过对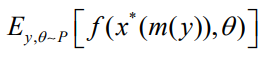 中的目标运行梯度步来直接训练预测模型
中的目标运行梯度步来直接训练预测模型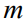 ,该目标融合了预测和优化。当前面临的直接困难在于对
,该目标融合了预测和优化。当前面临的直接困难在于对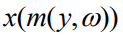 的依赖。这一术语存在两个问题。首先,它是一个离散量,因为是来自二进制集合的一个决策,这直接导致输出相对于模型参数
的依赖。这一术语存在两个问题。首先,它是一个离散量,因为是来自二进制集合的一个决策,这直接导致输出相对于模型参数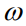 不可微。其次,即使
不可微。其次,即使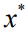 是连续的,它仍然被定义为优化问题的解,因此计算梯度需要本文通过
是连续的,它仍然被定义为优化问题的解,因此计算梯度需要本文通过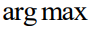 操作进行微分。
操作进行微分。
本文通过考虑组合决策问题的连续松弛来解决这两个困难。本文证明,对于一大类组合问题,存在适当的连续松弛,使得本文可以分析地获得连续优化器相对于模型参数的导数。这使本文能够通过在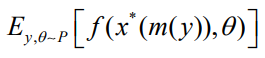 的连续替代项上应用梯度下降来训练任何可微分的预测模型。在测试时,本文通过将连续点四舍五入来解决真正的离散问题。
的连续替代项上应用梯度下降来训练任何可微分的预测模型。在测试时,本文通过将连续点四舍五入来解决真正的离散问题。
更具体地说,本文将离散约束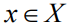 放宽到连续约束
放宽到连续约束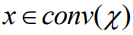 ,其中conv表示凸包。设
,其中conv表示凸包。设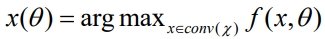 表示连续问题的最优解。为了训练本文的预测模型,本文希望计算由
表示连续问题的最优解。为了训练本文的预测模型,本文希望计算由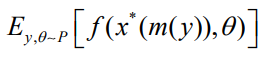 给出的整个管道目标的梯度,其中用连续的
给出的整个管道目标的梯度,其中用连续的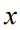 替换离散的
替换离散的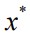 。本文可以通过从训练数据中采样一个单一的
。本文可以通过从训练数据中采样一个单一的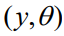 来获得随机梯度估计。在这个样本上,链式法则给出
来获得随机梯度估计。在这个样本上,链式法则给出
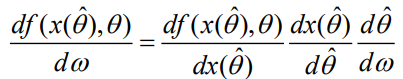
第一项是目标相对于决策变量x的梯度,最后一项是模型预测相对于其自身内部参数化的梯度。
关键是计算中间项,它衡量最优决策相对于预测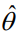 的变化。对于连续问题,最优连续决策x必须满足KKT条件(对于凸问题是充分的)。KKT条件定义了基于最优点附近的目标和约束梯度的线性方程组。已知通过应用隐函数定理,本文可以对这个线性系统的解进行微分。更详细地说,回想一下,本文的连续问题是在
的变化。对于连续问题,最优连续决策x必须满足KKT条件(对于凸问题是充分的)。KKT条件定义了基于最优点附近的目标和约束梯度的线性方程组。已知通过应用隐函数定理,本文可以对这个线性系统的解进行微分。更详细地说,回想一下,本文的连续问题是在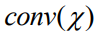 上进行的,即离散可行解的凸包。这个集合是一个多面体,可以通过线性等式表示为集合
上进行的,即离散可行解的凸包。这个集合是一个多面体,可以通过线性等式表示为集合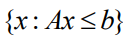 ,其中
,其中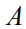 是某个矩阵,
是某个矩阵,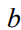 是向量。设
是向量。设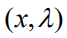 为满足KKT条件的原始和对偶变量的对。然后,对条件进行微分得出
为满足KKT条件的原始和对偶变量的对。然后,对条件进行微分得出
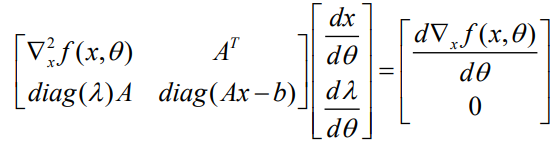
通过求解这个线性方程组,本文可以得到所需的项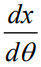 。然而,上述方法是一个通用框架;本文的主要技术贡献是为其应用于特定类别的组合问题提供实例。具体来说,本文需要
。然而,上述方法是一个通用框架;本文的主要技术贡献是为其应用于特定类别的组合问题提供实例。具体来说,本文需要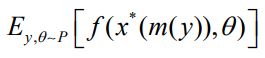 适当的连续松弛,以及解决连续优化问题的方法,以及上述公式在反向传播(即梯度计算)中有效访问等式2中所需的项。本文为两大类问题提供了这两个要素:线性规划和子模最大化。在每个设置中,高级挑战是确保连续松弛是可微的,这是朴素替代方案所不具备的特征。
适当的连续松弛,以及解决连续优化问题的方法,以及上述公式在反向传播(即梯度计算)中有效访问等式2中所需的项。本文为两大类问题提供了这两个要素:线性规划和子模最大化。在每个设置中,高级挑战是确保连续松弛是可微的,这是朴素替代方案所不具备的特征。
<1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;">6实验验证1>
6.1实验设置
本文实验主要在预算分配、二分图匹配与多样化推荐三个领域中进行对比。其中在每个领域中,随机将实例分为80%的训练集和20%的测试集,所有结果基于30次随机划分的平均值。使用前馈全连接神经网络作为底层预测模型,所有网络使用ReLU激活函数,且实验用一层网络代表一个受限的预测模型,两层网络代表表达能力更强的模型。
实验模型:
决策聚焦方法:提出的决策聚焦训练策略。
两阶段方法:使用机器学习损失函数(回归任务使用均方误差,分类任务使用交叉熵损失),这允许本文隔离训练方法的影响,因为两者使用相同的底层架构。
随机森林决策:使用神经网络完成任务的决策。
其中具体模型如下:
NN1-Decision:1层决策聚焦网络。
NN2-Decision:2层决策聚焦网络。
NN1-2Stage:1层两阶段网络。
NN1-2Stage:2层两阶段网络。
RF-2Stage:100棵决策树的随机森林集合。
6.2实验结果
决策质量如下图,在预算分配和多样化推荐任务中,根据预算的不同而变化。决策聚焦方法在所有领域中都获得了最高的性能,在合成预算分配任务中与随机森林持平。预算分配领域:两种决策聚焦方法都显著优于两阶段神经网络,获得至少37%的更高目标值。这表明在固定预测架构下,决策聚焦学习可以大大提高解决方案的质量。NN1-Decision的性能略优于NN2-Decision,表明更简单的模型类更容易训练。然而,NN1-2Stage的性能显著差于NN1-Decision,这表明训练与决策问题之间的对齐对于简单模型的成功至关重要。

除此之外,本文还通过均方误差(MSE)、交叉熵损失(这是两阶段网络直接优化的目标)和AUC测试了不同模型的预测效果,结果如下图。
<1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;"><1 style="text-wrap-style: initial;">1>1>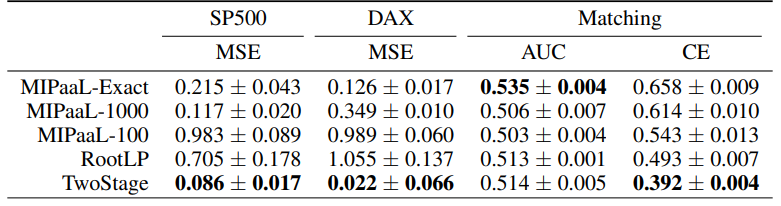
<1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;"><1 style="text-wrap-style: initial;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;"><1 style="text-wrap-style: initial;">尽管两阶段方法在大多数情况下在准确性上显著优于决策聚焦网络,但其解决方案的质量却较差。此外,没有一种准确性指标与解决方案质量具有良好的相关性。在预算分配上,两个决策聚焦网络的MSE最差,但解决方案质量最好。在双边匹配上,NN2-2Stage的交叉熵损失更低,但解决方案质量远逊于NN2-Decision。在多样化推荐上,NN2-2Stage的AUC最高,但解决方案质量不如任何决策聚焦网络。1>1>1>1>
<1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;">1>1>1><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;">7 1>1>1>1><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;text-wrap: wrap;">总结1>1>1>
<1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;"><1 style="text-wrap-style: initial;"><1 style="color: rgb(0, 0, 0);font-family: 微软雅黑;font-size: 15.04px;letter-spacing: 1px;"><1 style="text-wrap-style: initial;">本文提出了一种决策聚焦学习框架,旨在通过将机器学习模型直接与优化算法结合,来解决组合优化问题,并生成高质量的决策。该框架通过将离散优化问题连续松弛化,使得可以通过梯度下降等方法训练预测模型。文章具体针对线性规划和次模函数最大化两类广泛的组合问题实例化了这一框架。实验结果表明,与基于传统方法的两阶段优化相比,决策聚焦学习方法在多个领域的优化性能上通常表现得更好。此外,文章还发现,标准的预测准确性度量并不靠谱,不能作为预测模型在优化中效用的可靠代理。通过将模型训练目标设定为真正的优化目标,可以在一系列决策问题中获得显著的改进。1>1>1>1>