1)了解MATLAB Simulink的组成; 2)掌握线性系统Simulink仿真模型的建立方法; 3)通过典型环节阶跃响应的仿真,了解典型环节的动态特性; 4)了解MATLAB进行线性系统仿真的相关函数,编写线性系统仿真程序。 |
1.典型环节 典型环节主要包括:比例环节(K)、积分环节(1s)、惯性环节(1Ts+1)、理想微分环节(s)、实际微分环节(0)和振荡环节()等。各环节中特征参数的变化决定了系统具有不同的动态过程,例如:振荡环节的动态过程与其两个特征参数,即:自然频率和阻尼比有关。本实验主要任务之一是针对上述几种典型环节的传递函数,通过simulink仿真模型,观察各环节的动态响应特性,并分析动态过程随着参数变化而发生的改变。 2.matlab仿真程序 可以通过结构图的等效变换或者梅逊公式求解系统的传递函数,例如,可以求出下图中= G1sG2(s) 1+G1sG2sHs+G1sG2(s)2; =G2sG3s-(1+G1sG2(s)H(s))1+G1sG2sHs+G1sG2(s)
实际上当系统较为复杂时,也可以采用matlab程序的方式计算系统的传递函数,求解系统的零点、极点、增益等关键系统参数,以及分析系统的动态响应等等。本实验的另一个主要任务是,学习编写控制系统仿真及参数计算的matlab程序。相关matlab函数主要包括:tf(),zpk(),pzmap(),series(), parallel(), feedback(),impulse(),step()等。 |
1)熟悉MATLAB的基本使用方法,了解MATLAB的基本数学函数及用法; 2)掌握典型环节的传递函数; 3)安装MATLAB(包括“Control System Tookbox”模块)的个人电脑。 |
1.比例环节
Figure 1比例环节仿真模拟图 2.积分环节
Figure 2积分环节仿真模拟图 3.惯性环节
Figure 3惯性环节仿真模拟图 4.实际微分环节
Figure 4实际微分环节仿真模拟图 5.振荡环节
Figure 5振荡环节仿真模拟图(Wn不变)
Figure 6振荡环节仿真模拟图(ξ不变) 6.matlab控制系统仿真程序 (A) 用 tf 或 zpk 函数生成G1、G2、G3、H传递函数模型,其中 H 中令时间常数为0.5
Figure 7使用tf或zpk函数生成的传递函数模型 (B1)该传递函数的零点和极点
Figure 8该函数的零点与极点 (C1)改为1后,系统稳定
Figure 9改成1后,该系统稳定 (B2)该传递函数的零点和极点,可见下图
Figure 10该函数的零点和极点(见下图) (C2)改为1后,系统稳定
Figure 11改成1后,系统稳定 |
1.对于典型环节方面的实验,有以下五个分析: ①比例环节:由以上阶跃响应波形图知,比例环节使得输出量与输入量成正比,既无失真也无延迟,响应速度快,能对输入立即做出响应,因此系统易受外界干扰信号的影响,从而导致系统不稳定。 ②积分环节:由以上阶跃响应波形图知,积分环节的输入量反映了输入量随时间的积累,积分作用随着时间而逐渐增强,其反映速度较比例环节迟缓。 ③惯性环节:由以上单位阶跃响应波形图知,惯性环节使得输出波形在开始时以指数曲线上升,上升速度与时间常数(当中的s的系数)有关。 ④实际微分环节:由以上单位阶跃响应波形图知,微分环节的输出反映了输入信号的变换速度,即微分环节能预示输入信号的变化趋势,若输入为一定值,输出为零。 ⑤振荡环节:由以上单位阶跃响应波形图知,振荡环节的图像与Wn和ξ有关,当Wn一定时,ξ与振荡峰值有关。当ξ一定时,Wn与振荡时间有关。 2. 对于matlab仿真程序方面的实验,有以下三个分析: ①可以通过matlab的tf和zpk函数生成传递函数。 ②可以通过matlab的程序求得函数的零点和极点。 ③可以通过matlab的程序来求得有一个输入时,该传递函数对应的响应图像。 |
本次实验我熟悉了matlab桌面和命令窗口,初步了解simulink功能模块的使用方法。Matlab中simulink是一个用来对动态系统进行建模、仿真和分析的软件包,利用simulink功能模块可以快速的建立控制系统的模型进行仿真和调试。 在实验中,我通过simulink功能模块建立控制系统各个典型环节的模型,进行仿真和调试,得到了各个典型环节在单位阶跃信号作用下的响应波形,通过观察各个典型环节在单位阶跃信号作用下的动态特性,我定性的了解各参数变化对典型环节动态特性的影响,同时也加深了我对各典型环节响应曲线的理解。此外,我还通过matlab仿真程序求得对应的响应图,我认为这一个实验是本次实验当中难度最大,也是用处最大的一个实验。 |
Figure 12仿真图
Figure 13响应图 从左到右依次为ξ=-1、-0.5、0、1、2,对应的响应图。可以通过图像分析出改变ξ对函数的影响。
Figure 14延迟环节仿真模型
当时间常数趋于无穷大时,惯性环节可以近似地视为积分环节,当时间常数趋于0时,惯性环节可以近似地视为比例环节,可以根据公式推出。
% 以下是四个用于查找闭环极点的 MATLAB 函数: % 1. pole() % 此函数以传递函数或状态空间模型作为输入,并返回系统的极点。 function poles = find_poles(tf) poles = pole(tf); end % 2. rlocus() % 此函数以系统作为输入,并绘制系统的根轨迹。根轨迹可用于查找闭环极点。 function rlocus_plot(sys) rlocus(sys); end % 3. feedback() % 此函数以系统作为输入,并计算系统的闭环传递函数。闭环传递函数可用于查找闭环极点。 function closed_loop_tf = find_closed_loop_tf(sys) closed_loop_tf = feedback(sys); end % 4. step() % 此函数以系统作为输入,并绘制系统的阶跃响应。 function step_plot(sys) step(sys); end |
典型环节的仿真实验(自控实验一)
news/2024/11/7 19:22:36/
相关文章
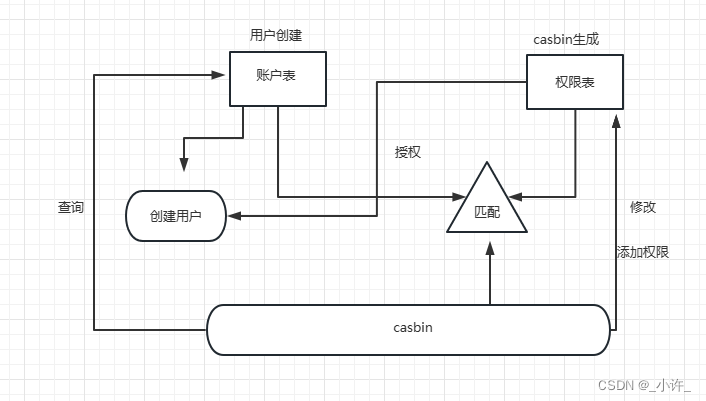
casbin基于RBAC模型实现权限管理
在casbin中权限都是基于匹配规则和访问控制模型实现的,除了上一章的ACL的实现方式,还有一个常用的访问控制模型RBAC。该模型带上了用户角色,基本满足大多数角色管理的系统。
在RBAC模型中多了一个角色的策略机制,其访问模型规则如…
全面解析缓存应用经典问题
1、前言
随着互联网从简单的单向浏览请求,发展为基于用户个性信息的定制化以及社交化的请求,这要求产品需要做到以用户和关系为基础,对海量数据进行分析和计算。对于后端服务来说,意味着用户的每次请求都需要查询用户的个人信息和…
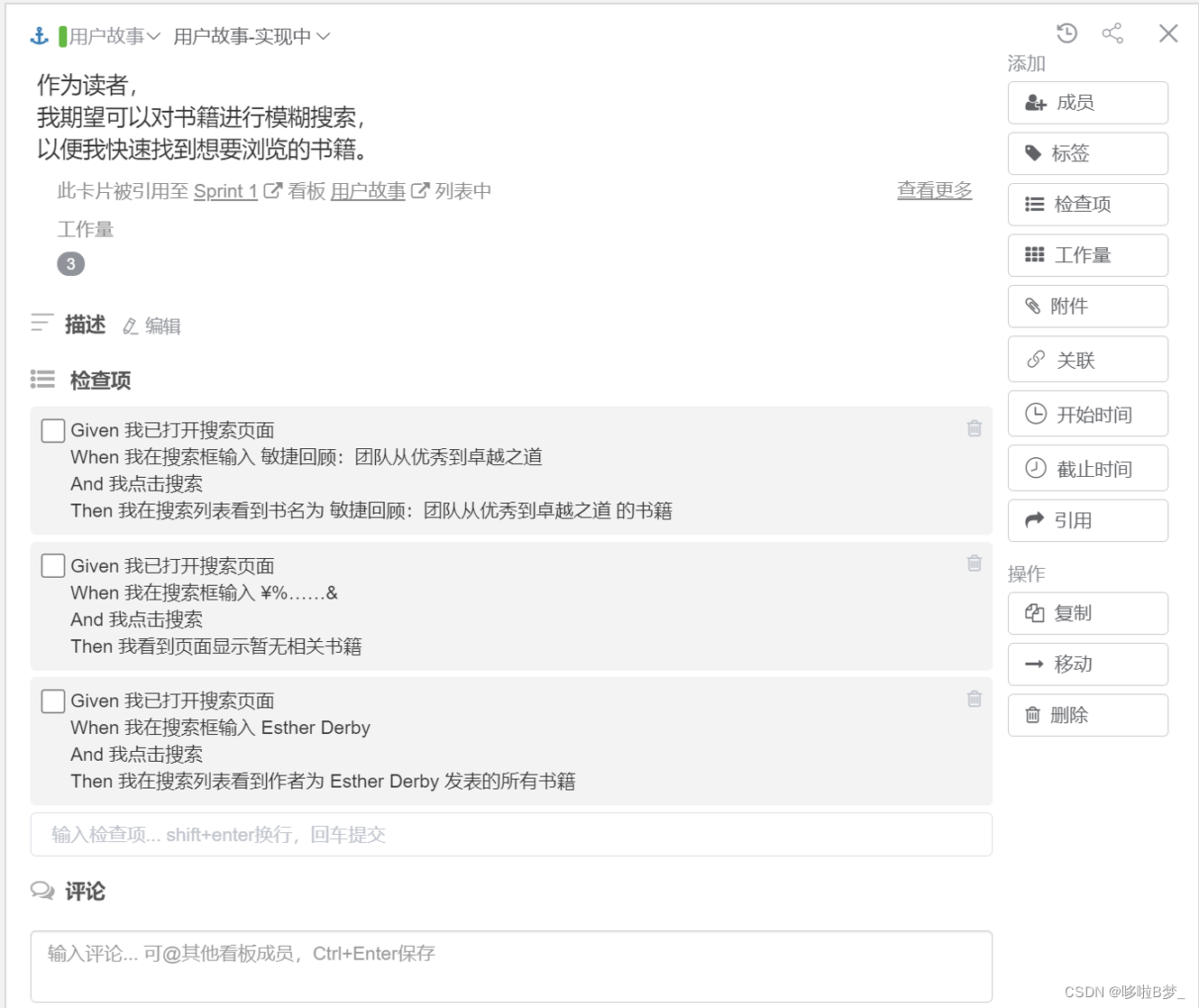
产品Backlog和需求管理
产品Backlog
产品backlog是一个按照价值排序的需求清单。为了达成产品目标,所有的需求都需要放到产品backlog中进行管理和规划。由产品负责人负责管理和维护。Leangoo为每一个里程碑建立了一个产品Backlog看板, 通过这个产品backlog看板来进行需求管理和规划。 里…
代码随想录训练营Day48|● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
目录
学习目标
学习内容 198.打家劫舍 213.打家劫舍II 337.打家劫舍III 学习目标 198.打家劫舍 213.打家劫舍II 337.打家劫舍III 学习内容 198.打家劫舍 198. 打家劫舍 - 力扣(LeetCode)https://leetcode.cn/problems/house-robber/ class Soluti…
2023门店管理系统app真实测评,第一款最实用!
我们在门店管理过程中,经常会遇到:库存管理不及时和不准确,订单处理不及时或出错,门店复购率低、客户流失严重等问题。 选用一款性价比高、实用性强、简单易操作的猛管理app,可以辅助我们更高效地管理门店,…
详解FreeRTOS:嵌入式多任务系统的任务等待和唤醒机制(理论篇—8)
当任务在试图访问IPC对象时,经常会因为运行条件不足而失败,被迫返回或者阻塞在该IPC对象的任务阻塞队列。而当有任务释放资源从而使得资源条件可以满足时,操作系统将会唤醒IPC对象上的阻塞任务,使得被唤醒任务继续运行。不同的访问…
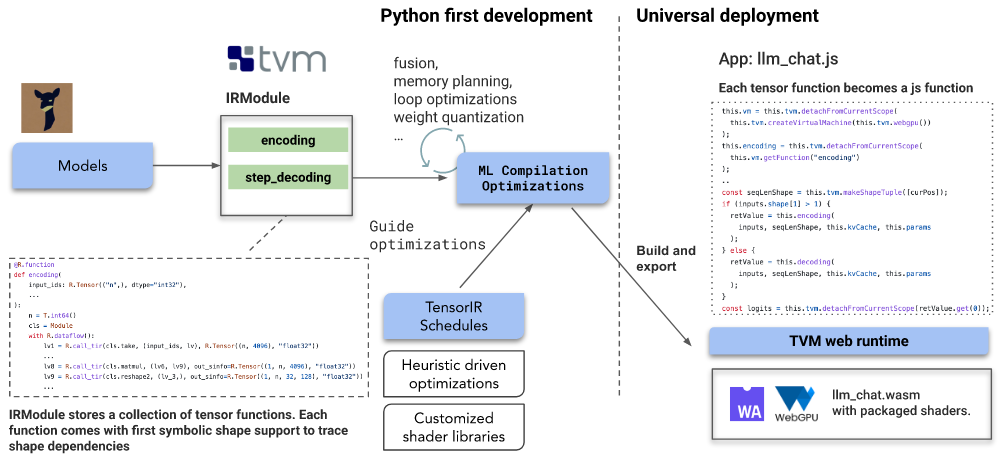
又一神器开源!无需服务器支持!打通手机,浏览器的Web LLM!
大家好,我是千与千寻,大家可以叫我“千寻哥”,之前和大家分享了两篇关于ChatGPT的技术文章,ChatGPT毫无疑问是现在最大的风口,各个行业都在集成ChatGPT的API接口以及各类的应用插件,这么多人的应用…
第一章.The Learning Problem
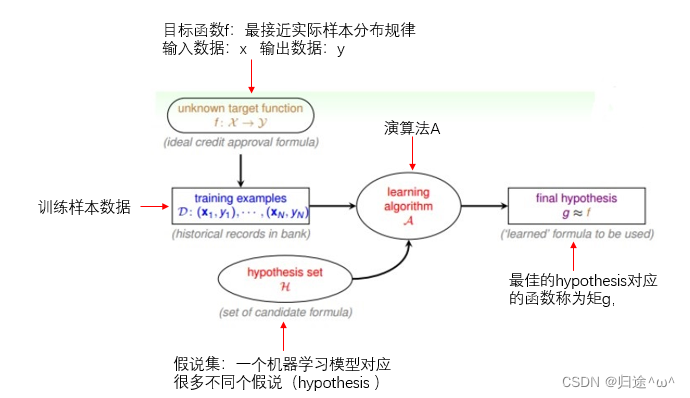
第一章.The Learning Problem 1.1 The Learning Problem 1.机器学习的概念:
机器学习就是机器从数据中总结经验。从数据中找出某种规律或者模型,并用他来解决某种实际问题。 2.机器学习的应用场景
1).事物本身存在某种潜在规律
2).某些问题难以使用普…