⛄一、小波变换心电信号去噪简介
0 引言
心电信号是人类最早研究的生物信号之一, 相比其他生物信号更易于检测, 且具有直观的规律。心电图的准确分析对心脏病的及早治疗有重大的意义。人体是一个复杂精密的系统, 有许多不可抗的外界因素, 得到纯净的心电信号非常困难。可以采用神经网络算法去除心电信号的噪声, 但这种方法存在训练难度大、耗时长的缺点。小波变换在处理非线性、非平稳且奇异点较多的信号时具有一定的优越性, 近年来许多学者使用其对心电信号进行研究。
1 心电信号简介
心电信号由以下几个波段组成, 一个典型的心电图如图1所示。

图1 典型心电图
(1) P波:反映心房肌在除极过程中的电位变化过程;
(2) P-R间期:反映的是激动从窦房结通过房室交界区到心室肌开始除极的时限;
(3) QRS波群:反映心室肌除极过程的电位变化;
(4) T波:代表心室肌复极过程中所引起的电位变化;
(5) S-T段:从QRS波群终点到达T波起点间的一段水平线[2];
(6) Q-T间期:心室从除极到复极的时间[3];
(7) U波:代表动作电位的后电位。
由于心电信号十分微弱, 且低频, 极易受到干扰, 不同的干扰源的噪声虽是随机的, 但来自同一个干扰源的噪声往往具有同一类特征。分析干扰的来源, 针对不同的来源使用合适的处理方法, 是数据采集重点考虑的一个问题。常见干扰有3种: (1) 工频干扰; (2) 基线漂移; (3) 肌电干扰。其中已经证明小波变换在抑制心电信号的工频干扰方面具有较大优势。具体噪声频带如表1所示。
表1 心电信号以及主要噪声频带

2 小波基础理论
2.1 小波变换定义

上述变换的逆变换为:

其中,


其中, a为尺度因子, b为位移因子, a, b∈R, 且a≠0, 当a, b不断变化时, 就可以得到一系列函数, 称为函数族, 在这里将这个函数族a, b (t) 称作小波基函数。小波变换的巧妙之处在于这个小波基函数中的a和b两个变量。a是将母小波进行伸缩变换, 且a在分母上, 所以a≠0。a越大, 母小波的时间域越大, 对应的频域越小, 适当将a增大可以用母小波研究低频信号, 提高时间域分辨率;a越小, 母小波的时间域越小, 对应频域越大, 适当减小a可以将母小波用来研究高频信号, 提高频率域的分辨率。b是位移因子, 调节b的大小可以将信号进行平移变换, 如果将a和b结合起来, 通过变换a和b的大小, 能对高频和低频信号都有一个好的分析效果。小波变换在时频域都是局部的, 能很好地对各时刻附近的频率信息进行处理。
2.2 Mallat算法
给定一个基本函数φ (x) , φ (x) 的伸缩和平移可以记为:

在小波变换中, 多分辨的一般定义为:L2 ® 可以被分割成许多小空间Vj, j=…, -2, -1, 0, 1, 2。
这样处理完之后, 就将L2 ® 这个向量空间用它的子空间Vj{j∈z}和Wj{j∈z}表示, 其中Vj{j∈z}被称为尺度空间, Wj{j∈z}被称为小波空间。
2.3 小波基的选择
首先选择对称性好的小波基, 对称性好的小波基不易产生相位畸变, 其次选择正则性好的小波基, 这样重构的信号更加平滑, 同时应该选择紧支撑的小波基使得处理能够实时进行。
Daubechies构造的db Nv小波就可以满足以上几个条件。其中最简单的是db1 (Haar) 小波, 但它的频域局域性差。此处选择db6小波, 相比db1小波其更加符合要求, 同时在MATLAB上容易实现, db6小波更接近于心电信号, 对心电信号去噪有更好的效果。图2为db系列小波基曲线。
3 小波去噪
3.1 去噪原理及评价标准
3.1.1 去噪原理
噪声的定义为“预测不到的, 只能用概率论统计的方法来认识的随机误差”。小波分析去噪的原理:对小波分解后的各层系数模大于和小于某阈值的系数分别进行处理, 然后利用处理后的小波系数重构出消噪后的图像[8]。将采集到的心电信号做多尺度的小波分解, 然后根据不同尺度的心电信号特征和噪声特点, 选取合适的规则, 利用分解的小波系数的特征在各尺度对心电信号进行去噪, 最后再进行重构, 得到去除噪声之后的图像。

图2 db系列小波
将心电信号进行小波变换之后, 在突变处幅值很大, 而突变的地方往往是噪声比较多的地方, 在很多比较平稳的有用信号处幅值很小, 这就能够用阈值的方法很好去除噪声。由前面的Mallat算法可以知道如何对信号进行多尺度分析, 即使信号突变严重, 也能用合适的小波系数将信号进行分解, 相比傅里叶单一的正弦函数基, 小波有很多优秀的小波基供选择去噪。
3.1.2 信号去噪的评价标准
信号去噪最好的结果是在不破坏信号本身信息的条件下将噪声予以剔除, 对原始信号的还原程度越高, 去噪效果越好。通常用以下两个参数来判断去噪效果的好坏:一个是最小化平均平方误差MSE, 另一个是信噪比SNR。

其中, X表示不含噪声的纯净的心电信号, x表示经过去噪过程之后的心电信号, 由式 (6) 可知, MSE越小, 真实纯净的信号与去噪之后的信号越接近, 去噪效果越好。

同样, X表示不含噪声的纯净的心电信号, 分母是均方误差, 分子是原始纯净的信号, SNR越大表明去噪效果越好。
除了这两个标准, 肉眼观察也可以辨别不同去噪算法的好坏, 本文最后的去噪效果通过客观和主观观察两种方法来判定。
3.2 阈值去噪
3.2.1 阈值去噪总流程
利用小波阈值去噪的过程如下:
(1) 选择一个合适的小波基;
(2) 利用下一小节式 (8) 确定分解的层数, 也可以利用简单规则, 根据SNR来简单确定分解层数;
(3) 根据小波系数, 选择合适的阈值对信号进行去噪;
(4) 将信号进行重构。
3.2.2 分解层数的选择
对信号处理的每一步都会影响最终的去噪结果, 分解层数过低或者过高都不能达到理想的去噪效果, 求解分解层数的公式为:

其中, fs是指所含噪声最低频率的下限。由上式中的几个变量可得, 分解层数j与采样频率、噪声频带宽度、信号长度这三个因素有关。
上述是求分解层数的最有效的方法, 也可以根据SNR来粗略确定分解层数, SNR越大, 可以选择相对较小的分解层数, 这样既能达到想要的去噪效果, 又能简化计算过程, 提高运算速度, 同理小的SNR时选择较大的分解层数才能达到想要的去噪效果。根据经验, 若SNR>20, 就可以将分解层数选为3, 既能有效去噪又能快速求解;若SNR<20, 可以粗略地将分解层数选为4。
3.2.3 阈值函数的选取
利用阈值去噪方法去除噪声过程中, 阈值的选取是最重要的一环, 传统的阈值选取方法有两种, 即硬阈值和软阈值。
首先介绍硬阈值的阈值取法, 硬阈值的取法如下所示:

其中, w为小波系数的值, 而λ为选定的阈值, 硬阈值即将小波系数中大于给定阈值的保持不变, 小于给定阈值的将其置0。硬阈值的处理效果在阈值点处一定是不连续的, 如果直接对信号进行重构, 那么重构的信号可能会产生震荡。
第二种阈值方法为软阈值:

此式中各符号的含义与硬阈值一样, 如果小波系数w比所设定的阈值大或者与设定的阈值相同时, 并不直接保留小波系数的值, 而是采取了一种比较平滑的处理, 令其为原值减阈值λ;小于时, 与硬阈值一样, 将其置0。经过这样的软阈值处理之后, 在阈值点处不会发生不连续的现象, 改进了硬阈值的缺点, 但对信号进行重构可能会影响重构信号对真实信号的逼近程度。软阈值相比硬阈值还是有更好的去噪效果, 因此本文基于软阈值来对信号去噪。
3.2.4 阈值选取
阈值去噪时在阈值大的情况下, 数据会不清晰, 大的阈值影响高频的小波系数, 心电信号边缘处小波系数被遗忘;若阈值选取值小, 会有很多噪声存在。可以采用全局和局部阈值, 用全部尺度或固定尺度的小波域系数仅以固定阈值进行噪声处理即全局阈值, 由小波系数的特征灵活地选择阈值即局部阈值。
全局阈值方法有:DJ阈值、极大极小阈值等。DJ阈值的D和J在理论上证明了当带有杂质的心电信号小波变换后, 如果其系数比指定阈值大时, 其含噪概率趋于0。其阈值选择标准如下:

其中, σn是噪声信号方差, N是信号长度。
但这种阈值处理效果并不理想, 会过度扼杀小波系数, 也会消除一些有用的小波信号。它只针对一个尺度上小波域系数的关联强度, 并没有在各个尺度表现小波系数的相关程度。
局部阈值挽救了全局阈值的不足, 把各个部位含噪信号的小波域系数的相关程度和杂质信号系数的影响也表示在公式中。分析小波系数的局部特点, 按照某种判定准则研究小波系数的来源, 决定是否保留这个小波系数。
⛄二、部分源代码
%%%%%%%%%%信号小波分解
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%基于Haar小波%%%%%%%
ecg=fopen(‘100.dat’,‘r’);
N=1201;
data=fread(ecg,N,‘int16’);
data=data/10000;
save ECGdata data;
fclose(ecg);
x=0:0.004:4.8;
figure(1);
subplot(321);
plot(x,data);
axis([0 4.8 -4 4]);
title(‘原始心电信号’);
x=data;
wname=‘Haar’;
level=5;
[c,l]=wavedec(x,level,wname);
a5=wrcoef(‘a’,c,l,‘Haar’,5);
a4=wrcoef(‘a’,c,l,‘Haar’,4);
a3=wrcoef(‘a’,c,l,‘Haar’,3);
a2=wrcoef(‘a’,c,l,‘Haar’,2);
a1=wrcoef(‘a’,c,l,‘Haar’,1);
subplot(322);plot(a5);title(‘a5’);axis([0 1201 -2 2]);
subplot(323);plot(a4);title(‘a4’);axis([0 1201 -2 2]);
subplot(324);plot(a3);title(‘a3’);axis([0 1201 -2 2]);
subplot(325);plot(a2);title(‘a2’);axis([0 1201 -2 2]);
subplot(326);plot(a1);title(‘a1’);axis([0 1201 -2 2]);
%%%%%%%%%%%%基于db6小波%%%%%
ecg=fopen(‘100.dat’,‘r’);
N=1201;
data=fread(ecg,N,‘int16’);
data=data/10;
fclose(ecg);
x=0:0.004:4.8;
figure(2);
subplot(321);
plot(x,data);
axis([0 4.8 -4000 4000]);
title(‘原始心电信号’);
x=data;
wname=‘db6’;
level=5;
[c,l]=wavedec(x,level,wname);
a5=wrcoef(‘a’,c,l,‘db6’,5);
a4=wrcoef(‘a’,c,l,‘db6’,4);
a3=wrcoef(‘a’,c,l,‘db6’,3);
a2=wrcoef(‘a’,c,l,‘db6’,2);
a1=wrcoef(‘a’,c,l,‘db6’,1);
subplot(322);plot(a5);title(‘a5’);axis([0 1201 -2000 2000]);
subplot(323);plot(a4);title(‘a4’);axis([0 1201 -2000 2000]);
subplot(324);plot(a3);title(‘a3’);axis([0 1201 -2000 2000]);
subplot(325);plot(a2);title(‘a2’);axis([0 1201 -2000 2000]);
subplot(326);plot(a1);title(‘a1’);axis([0 1201 -2000 2000]);
%%%%%%%%%%%%%%%%%基于sym3小波%%%%%%%%%%%%%%%%%%%%%%%
ecg=fopen(‘100.dat’,‘r’);
N=1201;
data=fread(ecg,N,‘int16’);
data=data/10;
save ECGdata data;
fclose(ecg);
x=0:0.004:4.8;
figure(3);
subplot(321);
plot(x,data);
axis([0 4.8 -4000 4000]);
title(‘原始心电信号’);
x=data;
wname=‘sym3’;
level=5;
[c,l]=wavedec(x,level,wname);
a5=wrcoef(‘a’,c,l,‘sym3’,5);
a4=wrcoef(‘a’,c,l,‘sym3’,4);
a3=wrcoef(‘a’,c,l,‘sym3’,3);
a2=wrcoef(‘a’,c,l,‘sym3’,2);
a1=wrcoef(‘a’,c,l,‘sym3’,1);
subplot(322);plot(a5);title(‘a5’);axis([0 1201 -2000 2000]);
subplot(323);plot(a4);title(‘a4’);axis([0 1201 -2000 2000]);
subplot(324);plot(a3);title(‘a3’);axis([0 1201 -2000 2000]);
subplot(325);plot(a2);title(‘a2’);axis([0 1201 -2000 2000]);
subplot(326);plot(a1);title(‘a1’);axis([0 1201 -2000 2000]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%心电信号降噪
%%%%%%%%%%%%%%%Birge-Massart策略阈值降噪
%基于小波变换的心电信号的降噪
ecg=fopen(‘100.dat’,‘r’);
N=1201;
data=fread(ecg,N,‘int16’);
data=data/10000;
fclose(ecg);
x=data;
wavename=‘db5’;
level=4;
[c,l]=wavedec(x,level,wavename);
alpha=1.5;
sorh=‘h’;
[thr,nkeep]=wdcbm(c,l,alpha);%使用硬阈值给信号降噪
[xc,cxc,lxc,perf0,perfl2]=wdencmp(‘lvd’,c,l,wavename,level,thr,sorh);
t1=0:0.004:(length(x)-1)*0.004;
figure(4);
subplot(211);
plot(t1,x);
title(‘从人体采集的原始的ECG信号’);
subplot(212);
plot(t1,xc);
title(‘Birge-Massart策略阈值降噪后的ECG信号(wname=db5 level=4)’);
%%%%%%%%%%%%%%%%%%最优预测软阈值降噪
%基于小波变换的心电信号的压缩
ecg=fopen(‘100.dat’,‘r’);
N=1201;
data=fread(ecg,N,‘int16’);
data=data/10000;
fclose(ecg);
x=data;
wavename=‘db3’;
level=4;
[xd,cxd,lxd]=wden(x,‘heursure’,‘s’,‘mln’,level,wavename);
t=0:0.004:4.8;
figure(5);
subplot(311);
plot(t,x);
title(‘从人体采集的原始的ECG信号’);
⛄三、运行结果




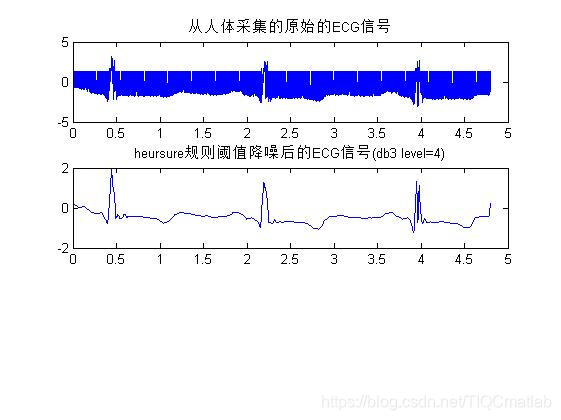


⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]焦运良,邢计元,靳尧凯.基于小波变换的心电信号阈值去噪算法研究[J].信息技术与网络安全. 2019,38(05)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除


![[高通MSM8909][Android7.1]电信卡信号优化](/images/no-images.jpg)