什么是博弈?字面描述中,博弈由两个字构成:博 和 弈。博弈是一种双方(多方)的对抗(比赛),对抗总是在一定的规则下进行,参与者必然会考虑应用相应的策略(计谋),并尽可能让自己获胜。
博弈论设计甚广,后续发展基本上沿着以下4个方面展开:
-
对 纳什均衡 的弱化(或一般化)研究
-
对 纳什均衡 的精炼(或筛选)研究
-
对 博弈论 的基本假设的深入研究
-
对 博弈论 的应用研究
事实上,博弈论早已从单纯对经济问题的研究发展成为对社会问题的研究,并且在经济学以外的政治学、社会学、管理学等众多领域都得到了广泛应用。
基于博弈论的重要性,针对 《博弈论》 一书进行了笔记摘要,相信博弈论将成为解释冲突、建立合作、增进信任、促进社会经济发展的重要理论。
文中讲述了多种博弈模型,贴近生活也耐人寻味。
一、概览
1)博弈类型和结构化思维
科学的起点是分类,只有通过分类才能区分事物之间的不同。
衣服会进行分类,书籍会进行分类,甚至身高、收入、智商等都能够进行分类。有了分类,事物才会变得有序。
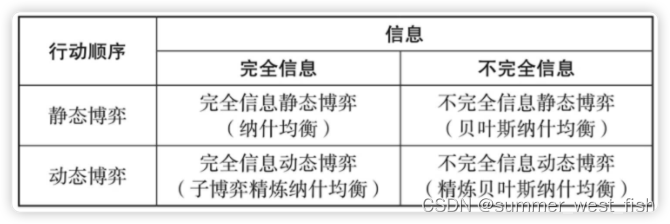
博弈的分类有两种:
-
静态博弈 和 动态博弈
-
完全信息博弈 和 不完全信息博弈
静态博弈和动态博弈
-
静态博弈是指在博弈中,参与者同时选择或虽非同时选择但后行动者并不知道先行动者采取了什么具体行动(虽然在物理时间上不是同时的,但是在逻辑时间上是同时的)
-
动态博弈是指在博弈中,参与者的行动有先后顺序,且后行动者能够观察到先行动者所选择的行动
以上推演到实际生活中:
石头剪刀布、投标活动就是 静态博弈
棋牌游戏、拍卖就是 动态博弈
有个实实在在的例子:
每个学校在课程结束后,都会要求学生给老师的课程评分,老师也需要对学生的成绩评分,如果学生先评分,那么可能会影响到老师做出成绩评分,如果老师先评分,那么可能也会影响到学生做出课程评分。那么这样一来,老师和学生之间就会相互牵制,难以确保评分真实有效。因此就会采取保密的方式,学生先评分,但是对老师保密,老师在进行学生成绩评分后的一段时间才能看到学生对自己的评分。而这就是一种 静态博弈 。
两者区别:
静态博弈 的参与者只能依据对对手策略或行动的想象做决策,比如 "石头剪刀布" 的游戏,你只能想象着对方会出"石头",然后你决定出"步"。
动态博弈 的参与者则是依据对手的实际选择做决策。
完全信息博弈与不完全信息博弈
-
完全信息博弈 是指在博弈过程中,每个参与者对其他参与者的类型、策略空间以及损益函数的信息都有准确的了解。
-
不完全信息博弈 就是与完全信息博弈相反,总有一些信息不是所有参与者都知道的。
以上推演到实际生活中:
教育、医疗和金融就是 不完全信息博弈
相比之下,完全信息博弈 少之又少,真实反映:生活本来就是不公平的
结构化思维
当某样东西可以从两个及以上不同的维度进行分类的时候,如果把两个维度组合在一个平面上,就可以构建出一种结构化的组合方式。
将上面说到4种博弈类型进行组合,我们可以得到:
2)扩展认知
纳什均衡
均衡是指所有博弈参与者的最优策略组合。
纳什均衡的释义就是:给定你的策略,我的策略就是对我而言最好的策略(或之一);给定我的策略,你的策略也是对你的来说最好的策略(或之一),双方在对方给定的策略下已经没有积极性调整自己已选的策略。
简言之:双方到了冷热化的底部,没有人愿意偏离自己给定的策略状态
策略探究
策略的三大属性:
1、策略的完整性
策略必须是完整的,意味着参与者把所有可能的情况都加以充分考虑,没有任何遗落(需善于利用分类,穷尽法)
2、策略的多样性
策略总是多样的,意味着你其实有很多个策略可以选择(A、B计划,留有一手,有备无患)
3、策略的不可观察性
策略不同于行动,行动是具体的做法,策略是对行动的预想。根据一个人的行为来推测一个人的策略有可能是错的(你以为的总是你以为的)
共同知识
什么是共同知识呢?
皇帝的新装 是一个家喻户晓的故事,但是皇帝没穿衣服,这是每个人都知道的 共有知识,但不是 共同知识,共同知识是每个人不但都知道(共有),而且也知道其他人都知道,而且都知道其他人知道每个人都知道...
我们平常所说的 共识 其实就是 共同知识 ,两者概念我们要加以区分。(不由想到互联网中著名的 两将军问题,TCP 为什么要进行 三次握手,而不是两次握手?就是为了达成共识)
二、经典模型
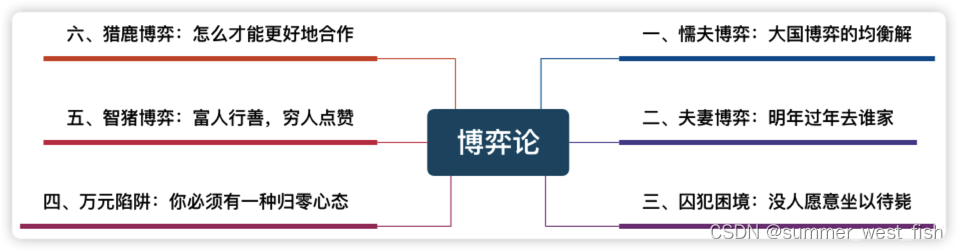
1)懦夫博弈
狭路相逢勇者胜 就是一种博弈,双方都在赌对方先退一步。
说起这种博弈,《速度与激情》中太多场景就是 懦夫博弈 的映照。
在懦夫博弈中,有两个参与者A和B,每个参与者有两种策略(行动):进和退。双方面临四种结果:都进、都退、A进B退、A退B进。
懦夫博弈存在先动优势,一旦有一方选择了进,另一方的选择只能是退,否则会遭到更大的损失,所谓的 **"先下手为强后下手遭殃"**。
从理论上来说,懦夫博弈的制胜策略是:抢先选择进,并抢先告诉对方已经选择了进,同时让对方知道自己的选择已经无法更改了
一句话中,体现了三要素:
-
抢先选择进
-
让对方知道自己选择了进
-
让对方知道自己没有退路
因此,懦夫博弈中的先动优势既是基于 行动的先动优势,又是基于信息传递的先动优势
赢者通吃会导致过度竞争,在这种博弈中,需要反复估量自己胜出的可能性,一般情况下选择不参与博弈是理性的。
2)夫妻博弈
夫妻间的博弈可谓不断,明年过年去谁家也成为了世纪难题。
这个问题的背景下,存在双方的共同利益。在夫妻博弈中,我们可以找到两个纯策略的纳什均衡:都去男方家过年或都去女方家过年。
从现实生活中分析,一般有三种情况:
-
与懦夫博弈一样存在先动优势,家庭地位决定纳什均衡的偏好
-
轮流去对方家
-
随机选择,这种解决方案比纳什均衡还有效,双方基于共同认可的规则。
提前商定合作收益的分配机制 :在所有的合作关系中,都会涉及合作收益的分配问题。不同的分配模式都有其存在的合理性,关键是合作之前先自愿约定,这样可以极大地降低合作成本。
夫妻博弈是一种共赢的合作博弈,但在合作的收益分配上存在差异。提前约定合作收益的分配是避免矛盾冲突的有效手段。
3)囚犯困境
囚犯困境又称“囚徒困境”,是博弈论中最为经典的理论模型之一。
囚犯困境在现在电视剧中屡见不鲜,大致场景为:两个罪犯进行分开审讯,如果两人都保持沉默,那么只能以犯罪事实定罪,可能判处的罪行就比较轻。但如果有一个人可以先坦白,那么这个人就可以当场释放,另一个人承受加重罪罚,如果两个人都坦白,不但不会被释放,还会加重处罚。
这个时候 囚犯困境 就出现了,对于两人来说最佳结果便是双方都选择抗拒,但对于个人来说便是先坦白,这才是占优策略
占优策略:采用该策略的结果都优于其他策略,由博弈中的所有参与者的占优策略组合所构成的均衡便是占优策略均衡
上述情境是在双方不能沟通的情况下,条件放宽后,允许两人呆上10分钟,再决定是否坦白。
那么此时博弈的方向就会变成双方是否遵守约定,当然,最好的选择依然是不遵守约定,最终的结果也取决于是否某一方能够具备在心理上不会有单独背叛对方的。
囚犯困境在现实中是无处不在的。对于囚犯困境的原因,人们一般理解为参与人对于自身利益的追求,因此有利益冲突的地方,往往就是一种囚犯困境。那么如何走出囚犯困境?
-
努力修改游戏规则。努力寻找每个人的占优策略,做不到让利于人,也要做到共利与人
-
寻求道德的力量。如果没有某种道德准则来约束人类的行为,那么人类社会与动物世界并无区别
-
借助历史的记忆。把对历史的记忆转为对未来的想象
囚犯困境的究极原因在于:每个人让自己利益增加,是以他人利益的更大损失为代价
囚犯困境带来的启示:博弈的均衡结果和事实的真相无关,只取决于博弈的规则
4)万元陷阱
这个博弈带来了一个十分有意思的案例:
有个《美元拍卖游戏》,在游戏中,苏必克把1美元纸币作为拍品,当众拍卖,拍卖的规则是:出价最高的人获得拍品,出价第二高的人也要付出所出价格的款项。
什么意思呢?现将10000元钱拍卖给大家,请大家互相竞价,以100元为加价单位,直到没有人再加价为止。出价最高者以其所出价格获得10000元钱,同时,出价第二高者也得将其所出价格的金钱数量付给我。
如果在场的人都没人参与竞拍,那么你只要以 100 元就可以获取到 10000元,净赚 9900 元。
当然以上是最佳的理想结果,如果有两人在不断加价,当你出到 1000 时,另一人出了 1100 ,你是否愿意放弃,如果你此时放弃就会损失 1000 元,那唯一的方法便是继续加价,冷热化持续中,当你已经加到 9900 元时,对方已经出价到了 10000 元,这个时候双方都不愿放弃,因此双方又在不断加价,甚至直到破产。
这就是著名的 万元陷阱 ,这些陷阱通常有三个特征:
-
一个明显的诱饵
-
通往诱饵之路是单向的,可进不可出
-
参与者越想挣脱就会陷得越深,变得不能自拔,最后为此付出惨痛的代价
那么如何避免 万元陷阱?
-
确立你投入的极限及预先的约定
-
极限一经确立,就要坚持到底,一定不要轻易改变
-
自己打定主意,尽量不受他人影响,避免出现 从众心理
-
不断提醒自己继续投入的代价
有趣的竞价方式:不要想着天上掉馅饼,直接开9900的价钱,只有100元的利润,一般情况下也不会有人继续加价,除非捣乱,但如果真的有人加价到 10000元,如果你决定继续加价,那就拿出 破釜沉舟 的行动,直接从 9900 加价到 19900 元,让对方意识到,如果再次加价到 20000 元,也是损失 10000 元,如果放弃也是损失 10000 元,而加价到 20000 元可能还会面临着你继续加价,增加损失。
避免万元陷阱最有效的策略就是及时止损,不要深陷其中,二是不要相信天上会掉馅饼,利小才不至于引起对方的强烈嫉妒和垂涎,如果血很多,会把狼招来的
5)智猪博弈
什么是智猪博弈呢?经典模型如下:
假设猪圈里有两头猪,一头大,一头小。猪圈的一侧放有食槽,另外一侧安装着控制猪食供应的按钮,按一下会有10个单位的猪食进槽,但是按动按钮的成本是2个单位的猪食。
情况1:如果两头猪一起按按钮,再一起跑过去吃,那么大猪会吃到 7 个单位,小猪吃到 3 个单位。减去成本,大猪:5,小猪:1
情况2:如果大猪去按按钮,小猪在食槽旁等着吃,那么大猪会吃到 6 个单位,小猪吃到 4 个单位。减去成本,大猪:4,小猪:4
情况3:如果小猪去按按钮,大猪在食槽旁等着吃,那么大猪会吃到 9 个单位,小猪吃到 1 个单位。减去成本,大猪:9,小猪:-1
3种情况很明显,对于小猪来说 等 是占优策略,那么在小猪一定等的情况下,想要吃到猪食,大猪只能按,那么这种情况的纳什均衡便是 (大猪按,小猪等)
但是这种均衡对大猪来说并不是占优策略,毕竟多劳并不能多得,最终的收益是(大猪:4,小猪:4)。在这个博弈模型中,对于小猪而言,无论如何都不会按按钮,大猪去不去按只影响小猪的损益,不会影响小猪的策略或行为选择。
因此这种模型也可以称为 搭便车博弈,一方付出了相应的代价,双方共享了所得到的收益。通过这种模型我们可以得到以下启示:
-
个体理性与集体理性是相互冲突,还是相一致,取决于制度安排本身。
-
收入分配的不均将有助于个体理性与集体理性的冲突。也就是让一部分人先富起来有助于帮助未富的人。
-
富人愿意行善,离不开穷人的点赞。想让大猪去按按钮,小猪可以选择少吃一点,让大猪觉得不会过于不平衡
-
能力越大,责任越大
在猜谜博弈中有两个非常重要的概念:纯策略 和 混合策略
纯策略: 参与者在每一个给定信息情况下只选择一种特定的行动
混合策略:参与者在给定信息情况下,以某种概率分布随机地选择不同的行动
比如“人不犯我,我不犯人;人若犯我,我必犯人”是一个纯策略。“人不犯我,我80%的可能性不犯人;人若犯我,我90%的可能性会犯人”就是一个混合策略
6)猎鹿博弈
又是一个有趣的博弈模型
两个人出去打猎,猎物为鹿和兔。
情况1:如果两个人独自去打兔子,一天下来可以打到2只兔子
情况2:如果要打鹿,则需要两个人一起去,缺一不可。(一只鹿的价值相当于8只兔子,每个人相当于4只兔子)当然如果只有一个人去打鹿,另一个没去,那么去打鹿的那个人收益为 0
分析发现,该模型下存在两种纳什均衡,便是要么一起去打鹿,要么一起去打兔子。
但是去打鹿就需要承担有一方未去打鹿的风险。那么这种情况下就需要 提前沟通
如果沟通成本小于最终获利成本,那么就要提前沟通,相互合作使利益最大化。沟通和协调成本越低,人与人之间就越容易建立合作关系