前言
今天在做一道宝石组合的题目时了解到了这个定理,还是蛮有意思的。
思想
唯一分解定理:
对于任何正整数n,有
n = p 1 a 1 × p 2 a 2 × . . . × p k a k n = p_1^{a1} \times p_2^{a2} \times ... \times p_k^{ak} n=p1a1×p2a2×...×pkak
其中,pi为质因子
基于这个定理,我们推广出关于最小公倍数(LCM)和最大公约数(GCD)的两个公式:
设两个正整数:n,m
l c m ( n , m ) = p 1 m a x ( a 1 , b 1 ) × p 2 m a x ( a 2 , b 2 ) × . . . × p k m a x ( a k , b k ) lcm(n,m) = p_1^{max(a1,b1)} \times p_2^{max(a2,b2)} \times... \times p_k^{max(ak,bk)} lcm(n,m)=p1max(a1,b1)×p2max(a2,b2)×...×pkmax(ak,bk)
g c d ( n , m ) = p 1 m i n ( a 1 , b 1 ) × p 2 m i n ( a 2 , b 2 ) × . . . × p k m i n ( a k , b k ) gcd(n,m) = p_1^{min(a1,b1)} \times p_2^{min(a2,b2)} \times... \times p_k^{min(ak,bk)} gcd(n,m)=p1min(a1,b1)×p2min(a2,b2)×...×pkmin(ak,bk)
同理可以推出:
n × m = l c m ( n , m ) × g c d ( n , m ) n \times m = lcm(n,m) \times gcd(n,m) n×m=lcm(n,m)×gcd(n,m)
宝石组合
题目
在一个神秘的森林里,住着一个小精灵名叫小蓝。有一天,他偶然发现了一个隐藏在树洞里的宝藏,里面装满了闪烁着美丽光芒的宝石。这些宝石都有着不同的颜色和形状,但最引人注目的是它们各自独特的 “闪亮度” 属性。每颗宝石都有一个与生俱来的特殊能力,可以发出不同强度的闪光。小蓝共找到了N 枚宝石,第 i 枚宝石的 “闪亮度” 属性值为 Hi,小蓝将会从这 N 枚宝石中选出三枚进行组合,组合之后的精美程度 S 可以用以下公式来衡量:
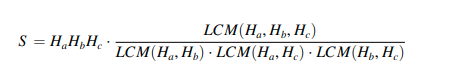
其中 LCM 表示的是最小公倍数函数。小蓝想要使得三枚宝石组合后的精美程度 S 尽可能的高,请你帮他找出精美程度最高的方案。如果存在多个方案 S 值相同,优先选择按照 H 值升序排列后字典序最小的方案。
题目分析
基于上面的分析,对给出的公式尝试化简:
S = ∏ i = 1 k p i a i + b i + c i × p i m a x ( a i , b i , c i ) p i m a x ( a i , b i ) × p i m a x ( a i , c i ) × p i m a x ( b i , c i ) S = \prod_{i=1}^{k} p_i^{a_i+b_i+c_i} \times \frac{p_i^{max(a_i,b_i,c_i)}}{p_i^{max(a_i,b_i)} \times p_i^{max(a_i,c_i)} \times p_i^{max(b_i,c_i)}} S=i=1∏kpiai+bi+ci×pimax(ai,bi)×pimax(ai,ci)×pimax(bi,ci)pimax(ai,bi,ci)
对上述式子进一步化简,可得:
S = ∏ i = 1 k p i a i + b i + c i × p i m a x ( 最大 ) p i m a x ( 最大 ) × p i m a x ( 最大 ) × p i m a x ( 次大 ) S = \prod_{i=1}^{k} p_i^{a_i+b_i+c_i} \times \frac{p_i^{max(最大)}}{p_i^{max(最大)} \times p_i^{max(最大)} \times p_i^{max(次大)}} S=i=1∏kpiai+bi+ci×pimax(最大)×pimax(最大)×pimax(次大)pimax(最大)
最后得到:
S = ∏ i = 1 k p i 最小 = ∏ i = 1 k p i m i n ( a i , b i , c i ) = g c d ( a , b , c ) S = \prod_{i=1}^{k} p_i^{最小} = \prod_{i=1}^{k} p_i^{min(a_i,b_i,c_i)} = gcd(a,b,c) S=i=1∏kpi最小=i=1∏kpimin(ai,bi,ci)=gcd(a,b,c)
所以经过化简公式,我们可以得出结论:就是找最大公约数最大的三个数
解答
经过上面的分析,我们有以下的思路:
- 1、定义一个fac二维数组,fac[i]是一个数组,表示i的所有约数
- 2、遍历所有a数组,s[a[i]]表示 a[i] 是哪些数的约数。
例如 10 的所有约数为 1 、 2、 5、 10
则
s[1] = { 10 }
s[2] = { 10 }
s[5] = { 10 }
s[10] = { 10 }
当我们遍历完a数组,倒着遍历s数组,第一次找到超过三个数的s[i],去前三项即是答案。
参考代码
#include<iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 100005;
vector<int> fac[N],s[N];
int a[N];
int main()
{int n;cin >> n;for(int i = 0;i<n;i++){cin >> a[i];}for(int i = 1; i<100005 ;i++){for(int j = i;j<100005;j+=i){fac[j].push_back(i);}}sort(a,a+n);for(int i = 0;i<n;i++){for(auto e : fac[a[i]]){s[e].push_back(a[i]);}}for(int i =100004;i>=0;i--){if(s[i].size() >= 3){cout << s[i][0] << " " << s[i][1] << " " << s[i][2] << endl;break;}}return 0;
}