数据结构 第六章 树与二叉树（三）

server/2024/12/22 2:09:22/

在这里插入图片描述

🚀 【考纲要求】二叉树的遍历
🚀 第六章第一节内容请查看此链接 树的基本概念
🚀 第六章第二节内容请查看此链接 二叉树的定义、四种特殊的二叉树和二叉树的存储结构

三、二叉树的遍历和线索二叉树

3.1二叉树的遍历

所谓的二叉树的遍历就是将按着某种顺序依次的遍历二叉树中的节点

从知识理解上看二叉树的遍历

①先序遍历

先序遍历就是按着根节点——左孩子节点——右孩子节点的顺序依次往下遍历

②中序遍历

是按着左孩子——根节点——右孩子的顺序遍历的

③后续遍历

按着左孩子——右孩子——根节点的顺序遍历

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

应该熟练的掌握这三种遍历的顺序，能够准确得出每种方法的遍历顺序。在遍历中我们还可以利用这些算法来求前缀、中缀和后缀表达式，使用先序遍历可以得到前缀表达式，使用中序遍历可以得到中缀表达式，使用后序遍历可以得到后缀表达式。
在这里插入图片描述
如何使用代码来表示这三种遍历顺序呢？其实就是使用了递归来实现遍历的，遍历之前要判断此时的根节点是否为空，即是否为空树，若不为空树就继续依次按着三种不同的访问顺序编写代码即可。

//先序遍历
void PreOrder(BiTree T){if(T!==NULL){visit(T);        //访问根节点PreOrder(T->Lchild);  //访问左孩子PreOrder(T->Rchild);  //访问右孩子}
}

//中序遍历
void PreOrder(BiTree T){if(T!==NULL){PreOrder(T->Lchild);  //访问左孩子visit(T);        //访问根节点PreOrder(T->Rchild);  //访问右孩子}
}

//后序遍历
void PreOrder(BiTree T){if(T!==NULL){PreOrder(T->Lchild);  //访问左孩子PreOrder(T->Rchild);  //访问右孩子visit(T);        //访问根节点}
}

④层序遍历

就是按着树的结构一层一层的遍历，对于这种方式的遍历我们是使用了一个队列进行辅助遍历的。
在这里插入图片描述
具体来看下它是怎么进行遍历的，首先判断是否为空树，树不为空，则将树的根节点首先入队；然后判断队列是否为空，若不为空则出队一个元素，与此同时判断出队元素的是否存在左孩子和右孩子，按着先入队左孩子再入队右孩子的顺序入队；入队操作结束后依次循环判队列空，出队一个元素，入队出对元素的左右孩子，值至队列空，遍历即可以完成。

在这里插入图片描述
⑤由遍历序列构造二叉树

前面学习了如何求一个树的遍历序列，接下去是给出中序的遍历序列和后续、先序、层序遍历中的一个来求特定的树的结构。

先来看一个例子
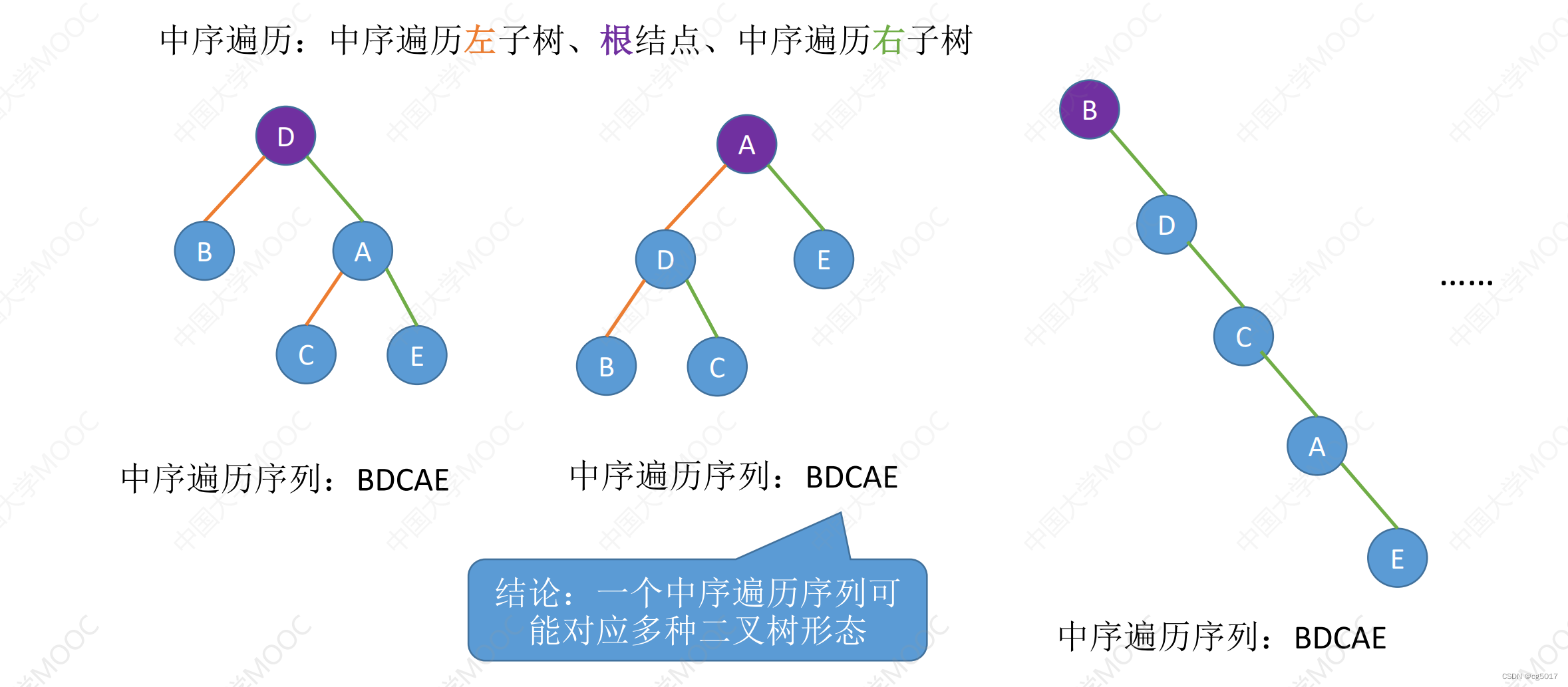
在这里插入图片描述
在这个例子中不难看出来若只给出一种遍历序列的话，其所能对应的树的结构是可以多种多样的，所以一种遍历序列是不可以推出具体树的结构的。所以能唯一可以确定树的结构的方法是中序遍历序列+先后层序遍历序列中一个才可以唯一的确定树的结构。

  • 中序遍历+先序遍历

在这里插入图片描述如上所示的遍历序列，为推出真实的树的结构，首先要确认根节点；由于先序遍历的第一个肯定是为根节点的，所以该树的根节点为A。由于根节点为A，再通过中序遍历序列就可得出BDC为左孩子的分支，E为右孩子的分支，即如下
在这里插入图片描述
接着继续分BDC；同样的要由先序遍历序列确定子树的根节点，显然子树的根节点为D，所以D为子树的根节点，再由中序遍历序列可知，D的左子树节点为B，右子树节点为C，即推出了正确的树结构
在这里插入图片描述

  • 中序遍历+后序遍历

在这里插入图片描述
遍历序列如上所示，仍然要先确认树的根节点，对于后续遍历来说，其最后遍历的肯定是根节点，所以该树的根节点为D，再由中序遍历序列就可推出其左子树为EAF，右子树为HCBGI。然后依次使用相同的步骤依次确认子树根节点，再确认根节点的左右子树。
在这里插入图片描述

  • 中序遍历+层序遍历

在这里插入图片描述
同样的要先找到树的根节点，由于层序遍历肯定由第一层开始遍历，即该树的根节点就是D，仍然由中序遍历序列确定左子树和右子树。根节点D，左子树EAF，右子树HCBGI；左子树根节点A，其左节点E，右节点为F；右子树根节点为B，其左子树为HC（根节点为C，左子树为H，无右子树），右子树为GI（根节点为G，无左子树，右子树为I）;所以最后的树如下所示：
在这里插入图片描述
以上就是由遍历序列推出子树的结构，而且也只有这三种序列的组合才可以推出树的结构，其余的组合是不能推出唯一确定的树的结构的。

从代码上看二叉树的遍历

文件结构：

在这里插入图片描述

①定义逻辑结构、初始化操作

Tree.h的内容

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int ElementType;typedef struct BitreeNode {ElementType data;  //数据域struct BitreeNode* LeftChild, * RightChild;  //左右孩子指针域int LeftTag, RightTag;   //标记指针是否指向左右孩子节点
}BitreeNode, * Bitree;//初始化二叉树
void IniateBitree(Bitree &tree,ElementType v);

Tree.c的内容

#include"Tree.h"//初始化二叉树
void IniateBitree(Bitree &tree,ElementType v) {BitreeNode* TreeNode = (BitreeNode*)malloc(sizeof(BitreeNode));assert(TreeNode);tree = TreeNode;tree->LeftChild = NULL;tree->RightChild = NULL;tree->LeftTag = 1;  tree->RightTag = 1;tree->data = v;
}

test.c的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,4);printf("根节点的数值为%d\n", tree->data);printf("根节点的左指针为%p\n", tree->LeftChild);printf("根节点的右指针为%p\n", tree->RightChild);return 0;
}

测试结果，初始化成功。

在这里插入图片描述

②构建一个二叉树

Tree.h的内容

//节点的插入
void InertBitreeNode(BitreeNode* Node, ElementType v, int i);

Tree.c的内容

//节点的插入
void InertBitreeNode(BitreeNode* Node, ElementType v, int i) {/* i为0时表示插在该节点的左孩子处i为1时表示插在该节点的右孩子处*/assert(Node);if ((i == 0) && (Node->LeftChild == NULL)) {BitreeNode* temp = (BitreeNode*)malloc(sizeof(BitreeNode));assert(temp);Node->LeftChild = temp;temp->data = v;temp->LeftChild = temp->RightChild = NULL;}else if ((i == 1) && (Node->RightChild == NULL)) {BitreeNode *temp = (BitreeNode*)malloc(sizeof(BitreeNode));assert(temp);Node->RightChild = temp;temp->data = v;temp->LeftChild = temp->RightChild = NULL;}else {printf("节点插入失败，位置不合法\n");exit;}
}

test.c的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);printf("根节点的数值为%d\n", tree->data);printf("根节点的左指针为%p\n", tree->LeftChild);printf("根节点的右指针为%p\n", tree->RightChild);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3printf("根节点的左孩子数值为%d\n", tree->LeftChild->data);InertBitreeNode(tree, 3, 1);  //根节点左孩子插3printf("根节点的右孩子数值为%d\n", tree->RightChild->data);InertBitreeNode(tree->LeftChild, 4, 1);printf("根节点的左孩子的右孩子数值为%d\n", tree->LeftChild->RightChild->data);InertBitreeNode(tree->RightChild, 5, 1);printf("根节点的右孩子的右孩子数值为%d\n", tree->RightChild->RightChild->data);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);printf("根节点的左孩子的右孩子的左孩子的数值为%d\n", tree->LeftChild->RightChild->LeftChild->data);return 0;
}

测试结果如下：
在这里插入图片描述

构建的二叉树的结构如下所示，接下去我们就要对我们构建的二叉树使用层序遍历、先序遍历、后续遍历、和中序遍历。
在这里插入图片描述
③先序遍历

Tree.h的内容

//visit函数
void visit(BitreeNode* Node);
//先序遍历
void PreOrder(Bitree tree);

Tree.c的内容

//visit函数
void visit(BitreeNode* Node) {printf("%d ", Node->data);
}//先序遍历 先访问根节点
void PreOrder(Bitree tree) {if (tree != NULL) {visit(tree);PreOrder(tree->LeftChild);PreOrder(tree->RightChild);}
}

test.c的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);printf("根节点的数值为%d\n", tree->data);printf("根节点的左指针为%p\n", tree->LeftChild);printf("根节点的右指针为%p\n", tree->RightChild);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3printf("根节点的左孩子数值为%d\n", tree->LeftChild->data);InertBitreeNode(tree, 3, 1);  //根节点左孩子插3printf("根节点的右孩子数值为%d\n", tree->RightChild->data);InertBitreeNode(tree->LeftChild, 4, 1);printf("根节点的左孩子的右孩子数值为%d\n", tree->LeftChild->RightChild->data);InertBitreeNode(tree->RightChild, 5, 1);printf("根节点的右孩子的右孩子数值为%d\n", tree->RightChild->RightChild->data);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);printf("根节点的左孩子的右孩子的左孩子的数值为%d\n", tree->LeftChild->RightChild->LeftChild->data);//先序遍历PreOrder(tree);return 0;
}

在这里插入图片描述
可以看到结果，采用先序遍历的结果其遍历节点的顺序是 1 2 4 5 6，我们在按着我们之前理解的方式来遍历一遍，首先是遍历根节点123，然后1243，然后12463，然后124635，和结果一致！！！

④中序遍历

Tree.h的内容

//中序遍历
void MidOrder(Bitree tree);

Tree.c的内容

//中序遍历
void MidOrder(Bitree tree) {if (tree != NULL) {MidOrder(tree->LeftChild);visit(tree);MidOrder(tree->RightChild);}
}

test.c的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);printf("根节点的数值为%d\n", tree->data);printf("根节点的左指针为%p\n", tree->LeftChild);printf("根节点的右指针为%p\n", tree->RightChild);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3printf("根节点的左孩子数值为%d\n", tree->LeftChild->data);InertBitreeNode(tree, 3, 1);  //根节点左孩子插3printf("根节点的右孩子数值为%d\n", tree->RightChild->data);InertBitreeNode(tree->LeftChild, 4, 1);printf("根节点的左孩子的右孩子数值为%d\n", tree->LeftChild->RightChild->data);InertBitreeNode(tree->RightChild, 5, 1);printf("根节点的右孩子的右孩子数值为%d\n", tree->RightChild->RightChild->data);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);printf("根节点的左孩子的右孩子的左孩子的数值为%d\n", tree->LeftChild->RightChild->LeftChild->data);//先序遍历PreOrder(tree);printf("\n");//中序遍历MidOrder(tree);printf("\n");return 0;
}

在这里插入图片描述

可以看到结果，采用先序遍历的结果其遍历节点的顺序是 2 6 4 1 3 5，我们在按着我们之前理解的方式来遍历一遍，首先是遍历213，然后2413，然后26413，然后264135，和结果一致！！！

⑤后续遍历
Tree.h的内容

//后序遍历
void PostOrder(Bitree tree);

Tree.c的内容

//后序遍历
void PostOrder(Bitree tree) {if (tree != NULL) {PostOrder(tree->LeftChild);PostOrder(tree->RightChild);visit(tree);}
}

test.c的内容

在这里插入图片描述
⑥层序遍历

Tree.h的内容

再加上以下头文件，因为层序遍历需要使用一个栈作为辅助，C++中可以直接定义一个栈，所示直接使用C++的语法来定义一个栈。

#include<iostream>
#include<queue>
using namespace std;//层序遍历
void LayerOrder(Bitree tree);

Tree.c的内容

//层序遍历
void LayerOrder(Bitree tree) {queue <BitreeNode *>s1;   //定义一个栈/*1.根节点入队*/s1.push(tree);  /*2.队列非空，出队并访问该节点，若该节点有左右孩子，依次入队。*/while (!s1.empty()) {BitreeNode* tmp = s1.front();s1.pop();visit(tmp);if (tmp->LeftChild != NULL) {s1.push(tmp->LeftChild);}if (tmp->RightChild != NULL) {s1.push(tmp->RightChild);}}
}

test.c的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);printf("根节点的数值为%d\n", tree->data);printf("根节点的左指针为%p\n", tree->LeftChild);printf("根节点的右指针为%p\n", tree->RightChild);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3printf("根节点的左孩子数值为%d\n", tree->LeftChild->data);InertBitreeNode(tree, 3, 1);  //根节点左孩子插3printf("根节点的右孩子数值为%d\n", tree->RightChild->data);InertBitreeNode(tree->LeftChild, 4, 1);printf("根节点的左孩子的右孩子数值为%d\n", tree->LeftChild->RightChild->data);InertBitreeNode(tree->RightChild, 5, 1);printf("根节点的右孩子的右孩子数值为%d\n", tree->RightChild->RightChild->data);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);printf("根节点的左孩子的右孩子的左孩子的数值为%d\n", tree->LeftChild->RightChild->LeftChild->data);//先序遍历PreOrder(tree);printf("\n");//中序遍历MidOrder(tree);printf("\n");//后续遍历PostOrder(tree);printf("\n");//层序遍历LayerOrder(tree);printf("\n");return 0;
}

在这里插入图片描述

3.2线索二叉树

在这里插入图片描述
对于上面的我们使用代码构建的二叉树来说，其2，3，4，5，6号节点的中的指针域并没有被用完，所以我们得用这些没有利用的空指针域来构建线索二叉树。

构建结果如下：
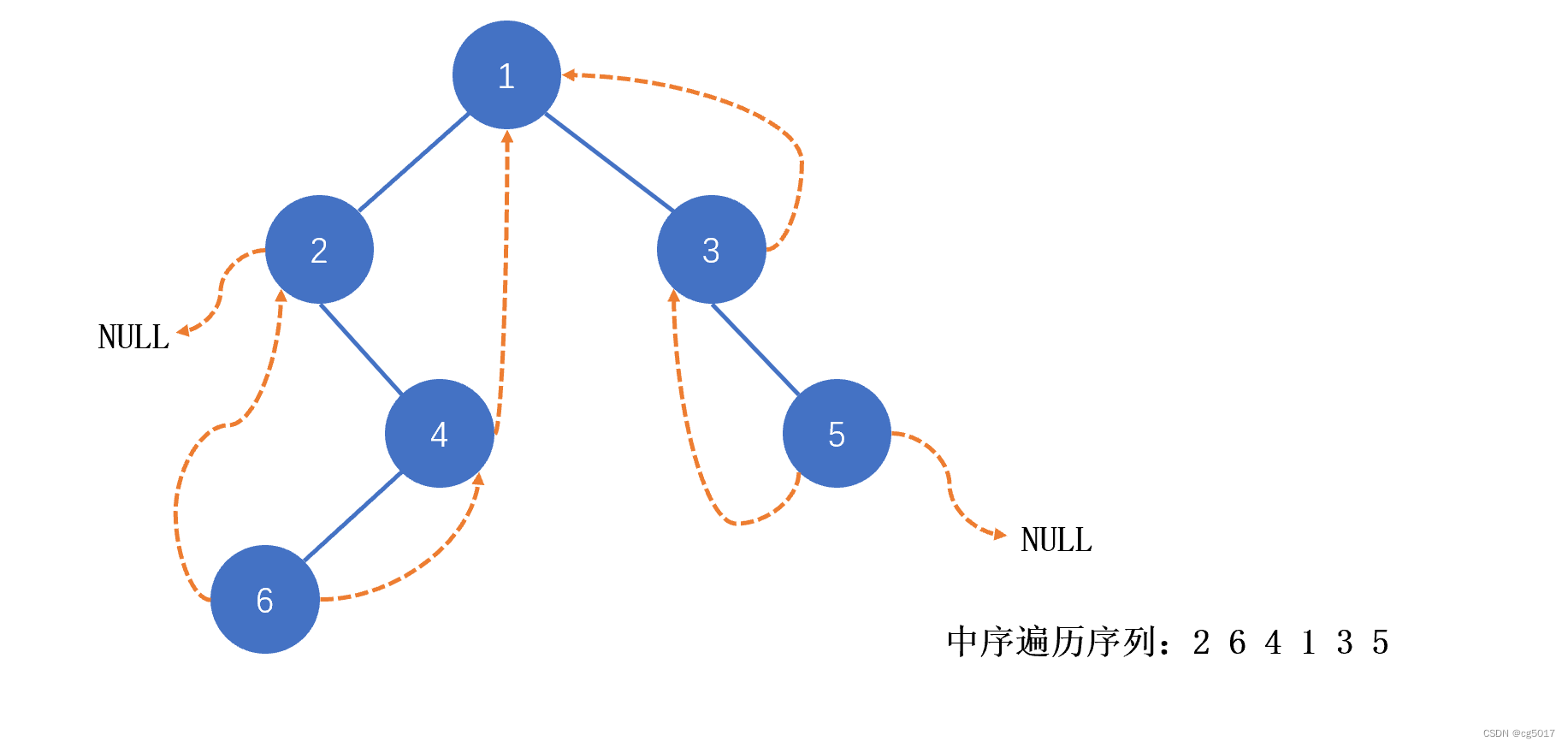
在这里插入图片描述

①理解线索二叉树构建的过程

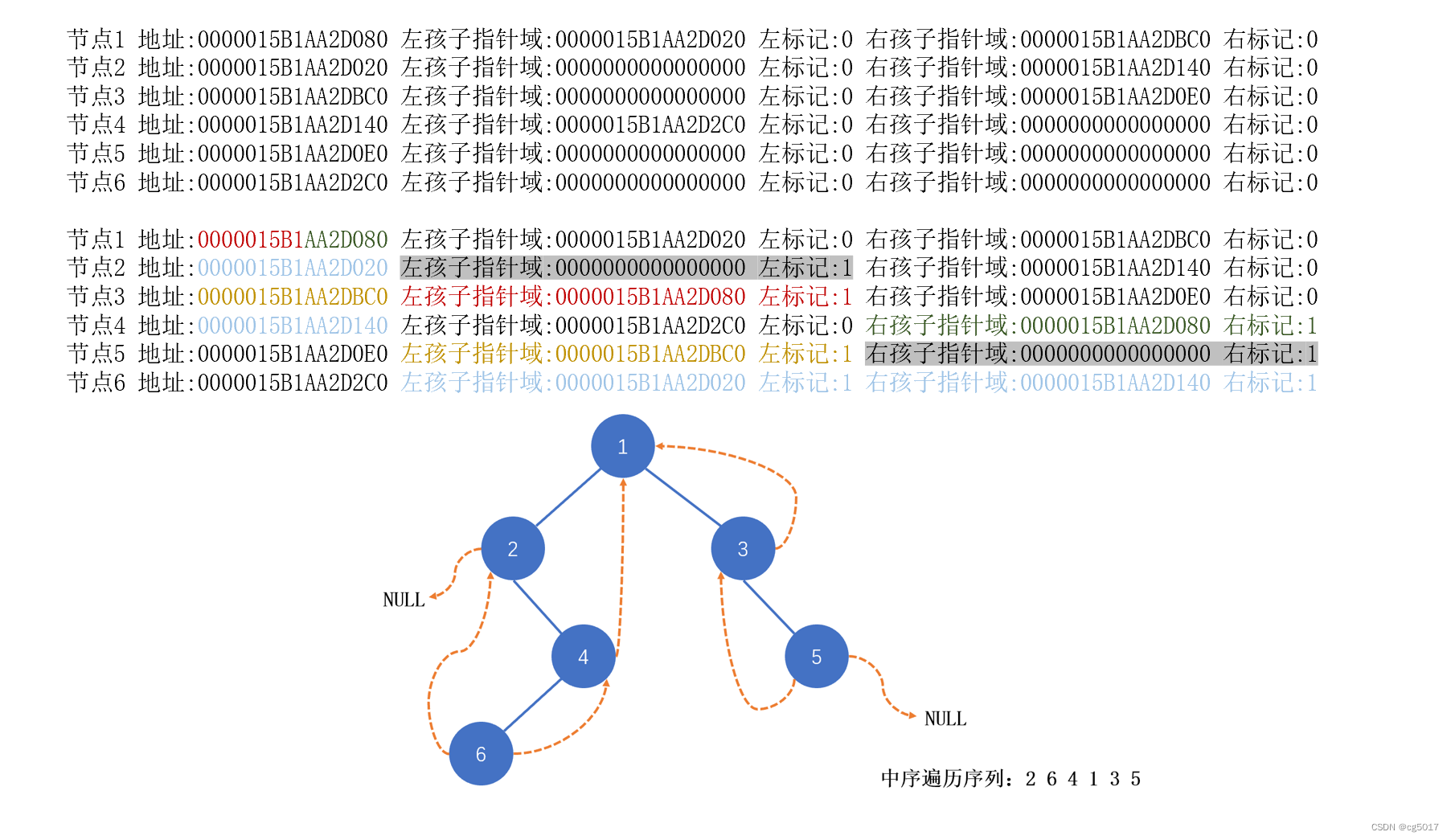
上述代码构建的二叉树，若使用中序遍历的话，其产生的中序遍历序列就为264135，对于中序遍历序列来说，我们其实可以将这个序列看成一个线性表，这个线性表除了头尾元素都有前驱和后继元素，而我们在构建线索二叉树时，就是利用空指针域来指向他们的前驱和后继元素。

来看一下以下这个二叉树是如何进行线索化的，现在我们以中序线索化为例

  • 利用pre指针指向访问当前节点的前驱节点，当访问第一个节点B的时候，P是指向B节点的，而pre要指向B节点的前驱节点，所以要先将pre指针赋为NULL。
  • 访问当前节点的时候进行两个判断
    • First：判断当前节点的左孩子指针域是否为空，若为空，则构建该节点的前驱线索，即让当前节点的左孩子指针域指向前驱节点（pre指向的位置）。（p -> LeftChild = pre; p -> LeftTag = 1）
    • Secend：判断当前pre在不为空的情况下所指向的节点的右孩子指针域是否为空，若为空，则将pre所指向的右孩子指针域赋为p。（pre -> RightChild = p; pre -> RightTag = 1）
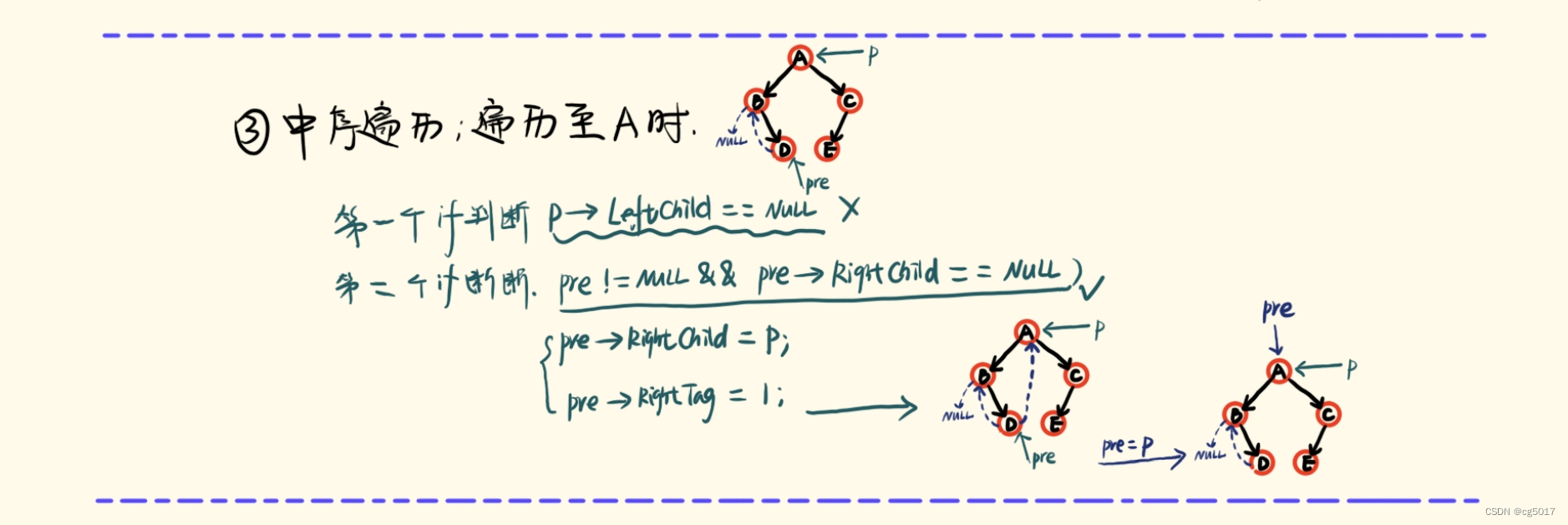
    • Third：判断结束后让pre=p。在这里插入图片描述在这里插入图片描述
      通过不断循环上述操作，直到遍历至二叉树中的最后一个元素为止。中序线索二叉树就构建完成了，那中序遍历完成是否中序线索二叉树真的构建完成了呢，我们来看一下遍历到最后一个节点的话，就是遍历至节点C，也就是P指向节点C，pre指向节点E时，进入条件判断，让pre -> RightChild = p; pre->RightTag=1，条件结束后，还有一个步骤Third步骤，让pre=p;，此时就遍历完成，同时，递归遍历结束；而此时的节点C的右孩子节点还未进行线序构建，所以递归最终结束之后还应该将pre->RightChild=NULL;。
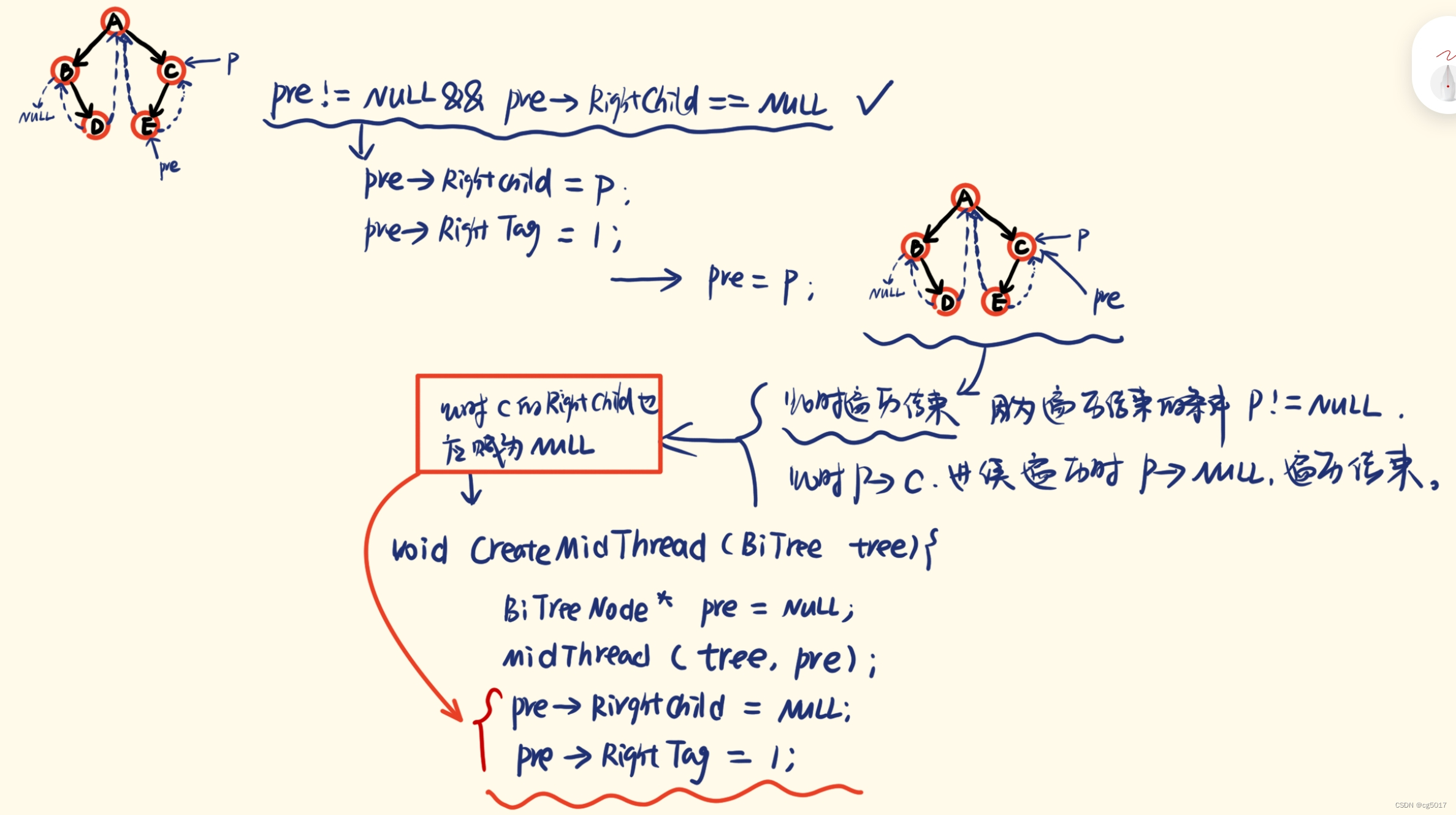
      在这里插入图片描述

②线索二叉树的代码实现

继续使用上述文件结构，将上述代码构建的二叉树结构，进一步构建为中序线索二叉树。
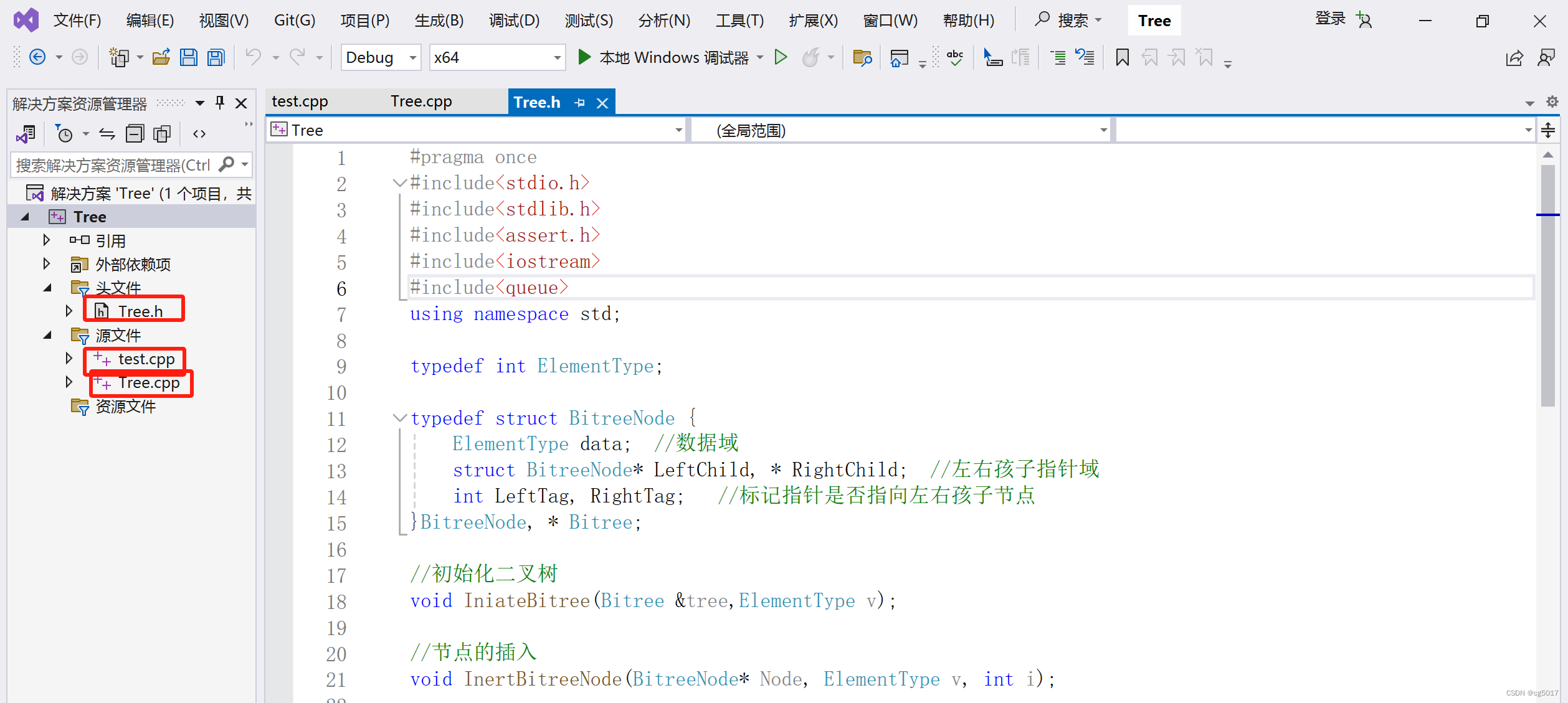
在这里插入图片描述

①准备待构建中序线索二叉树的二叉树

Tree.cpp的内容
节点插入的代码更改了一下，加上了每一次新增节点的时候将其左右tag都设置为1，表示不是构建线序的指针。

//节点的插入
void InertBitreeNode(BitreeNode* Node, ElementType v, int i) {/* i为0时表示插在该节点的左孩子处i为1时表示插在该节点的右孩子处*/assert(Node);if ((i == 0) && (Node->LeftChild == NULL)) {BitreeNode* temp = (BitreeNode*)malloc(sizeof(BitreeNode));assert(temp);temp->LeftTag = temp->RightTag = 0;Node->LeftChild = temp;temp->data = v;temp->LeftChild = temp->RightChild = NULL;}else if ((i == 1) && (Node->RightChild == NULL)) {BitreeNode *temp = (BitreeNode*)malloc(sizeof(BitreeNode));assert(temp);temp->LeftTag = temp->RightTag = 0;Node->RightChild = temp;temp->data = v;temp->LeftChild = temp->RightChild = NULL;}else {printf("节点插入失败，位置不合法\n");exit;}
}

test.cpp的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3InertBitreeNode(tree, 3, 1);  //根节点左孩子插3InertBitreeNode(tree->LeftChild, 4, 1);InertBitreeNode(tree->RightChild, 5, 1);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);//层序遍历LayerOrder(tree);printf("\n");return 0;
}

在这里插入图片描述
此时已经准备好了待构建的二叉树。

②中序线索二叉树

Tree.h的内容

//中序线索二叉树的构建
void CreateMidThread(Bitree &tree);//中序线索二叉树的遍历
void MidThread(Bitree &tree, BitreeNode* &pre);

Tree.cpp的内容

//visit函数
void visit(BitreeNode* Node) {printf("节点%d 地址:%p 左孩子指针域:%p 左标记:%d 右孩子指针域:%p 右标记:%d\n", Node->data,Node,Node->LeftChild,Node->LeftTag,Node->RightChild,Node->RightTag);
}

//中序线索二叉树的遍历
void MidThread(Bitree &tree, BitreeNode* &pre) {if (tree != NULL) {//左MidThread(tree->LeftChild, pre);   //根if (tree->LeftChild == NULL) {tree->LeftChild = pre;tree->LeftTag = 1;}if (pre != NULL && pre->RightChild == NULL) {pre->RightChild = tree;pre->RightTag = 1;}pre = tree;//右MidThread(tree->RightChild, pre);}}//中序线索二叉树的构建
void CreateMidThread(Bitree &tree) {assert(tree);BitreeNode* pre = NULL;MidThread(tree,pre);pre->RightChild = NULL;pre->RightTag = 1;
}

test.cpp的内容

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3InertBitreeNode(tree, 3, 1);  //根节点左孩子插3InertBitreeNode(tree->LeftChild, 4, 1);InertBitreeNode(tree->RightChild, 5, 1);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);//层序遍历LayerOrder(tree);printf("\n");CreateMidThread(tree);visit(tree); //根节点 1           visit(tree->LeftChild); // 2visit(tree->RightChild); // 3visit(tree->LeftChild->RightChild);  //4visit(tree->RightChild->RightChild); //5visit(tree->LeftChild->RightChild->LeftChild); //6return 0;
}

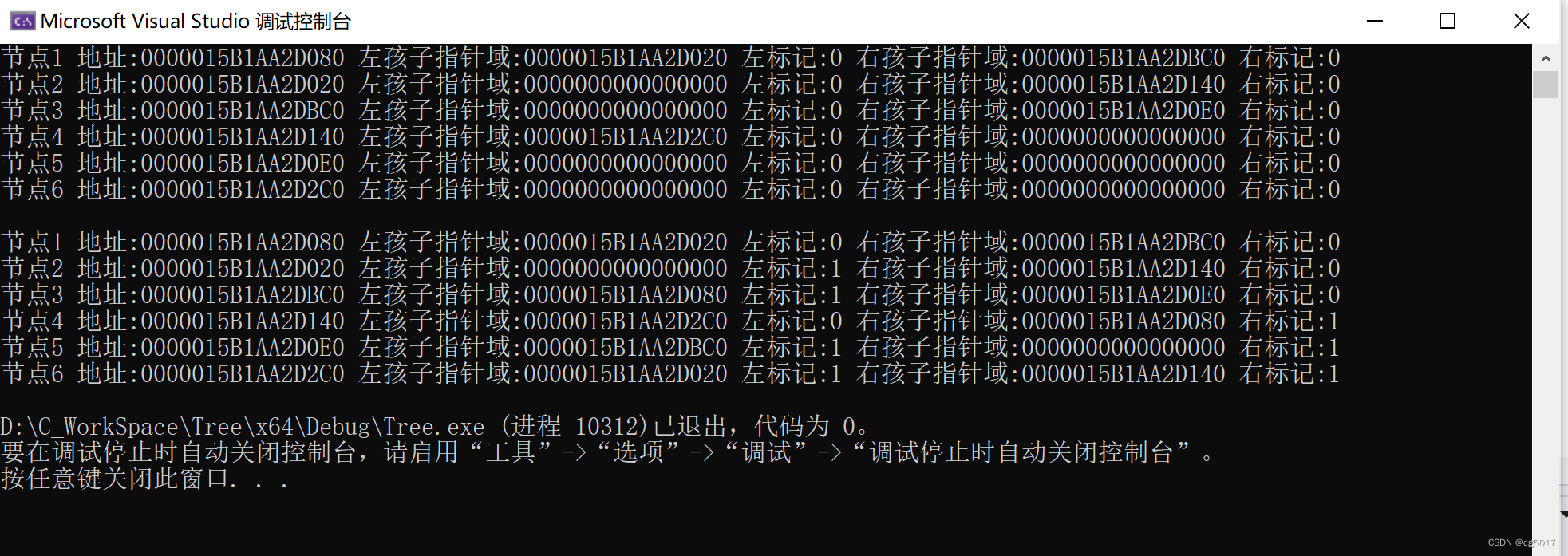
在这里插入图片描述

结果如下，构建完成。
在这里插入图片描述

③后序线索二叉树

Tree.h

//后序线索二叉树的构建
void CreatePostThread(Bitree& tree);
//后序线索二叉树的遍历
void PostThread(Bitree& tree, BitreeNode*& pre);

Tree.cpp

//后序线索二叉树的遍历
void PostThread(Bitree& tree, BitreeNode*& pre) {if (tree != NULL) {//左PostThread(tree->LeftChild, pre);//右PostThread(tree->RightChild, pre);//根if (tree->LeftChild == NULL) {tree->LeftChild = pre;tree->LeftTag = 1;}if (pre != NULL && pre->RightChild == NULL) {pre->RightChild = tree;pre->RightTag = 1;}pre = tree;}
}//后序线索二叉树的构建
void CreatePostThread(Bitree& tree) {assert(tree);BitreeNode* pre = NULL;PostThread(tree, pre);if (pre->RightChild == NULL) {pre->RightTag = 1;}
}

test.cpp

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3InertBitreeNode(tree, 3, 1);  //根节点左孩子插3InertBitreeNode(tree->LeftChild, 4, 1);InertBitreeNode(tree->RightChild, 5, 1);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);//层序遍历LayerOrder(tree);printf("\n");CreatePostThread(tree);visit(tree); //根节点 1           visit(tree->LeftChild); // 2visit(tree->RightChild); // 3visit(tree->LeftChild->RightChild);  //4visit(tree->RightChild->RightChild); //5visit(tree->LeftChild->RightChild->LeftChild); //6return 0;
}

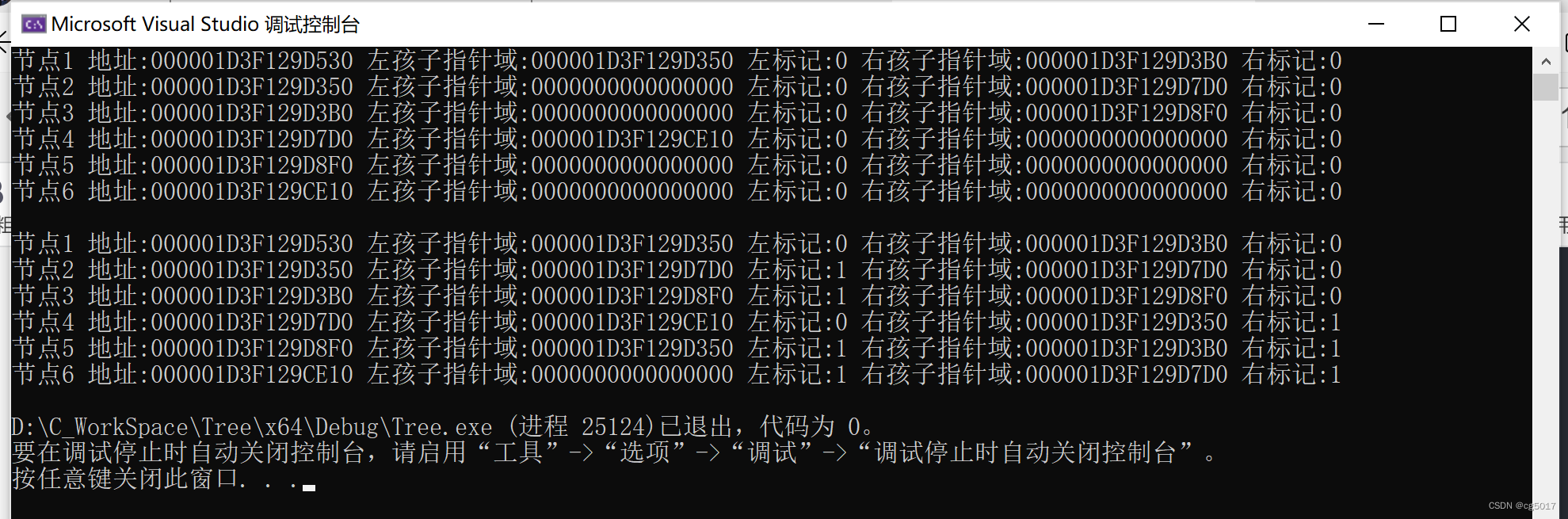
在这里插入图片描述
④先序线索二叉树

Tree.h

//先序线索二叉树的遍历
void PreThread(Bitree& tree, BitreeNode*& pre);
//先序线索二叉树的构建
void CreatePreThread(Bitree& tree);

Tree.cpp

//先序线索二叉树的遍历
void PreThread(Bitree& tree, BitreeNode* &pre) {if (tree != NULL) {//根if (tree->LeftChild == NULL) {tree->LeftChild = pre;tree->LeftTag = 1;}if (pre != NULL && pre->RightChild == NULL) {pre->RightChild = tree;pre->RightTag = 1;}pre = tree;//左if (tree->LeftTag == 0) {PreThread(tree->LeftChild, pre);}//右if (tree->RightTag == 0) {PreThread(tree->RightChild, pre);}}}//先序线索二叉树的构建
void CreatePreThread(Bitree& tree) {assert(tree);BitreeNode* pre = NULL;PreThread(tree, pre);pre->RightChild == NULL;pre->RightTag = 1;
}

test.cpp

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3InertBitreeNode(tree, 3, 1);  //根节点左孩子插3InertBitreeNode(tree->LeftChild, 4, 1);InertBitreeNode(tree->RightChild, 5, 1);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);//层序遍历LayerOrder(tree);printf("\n");CreatePreThread(tree);visit(tree); //根节点 1           visit(tree->LeftChild); // 2visit(tree->RightChild); // 3visit(tree->LeftChild->RightChild);  //4visit(tree->RightChild->RightChild); //5visit(tree->LeftChild->RightChild->LeftChild); //6return 0;
}

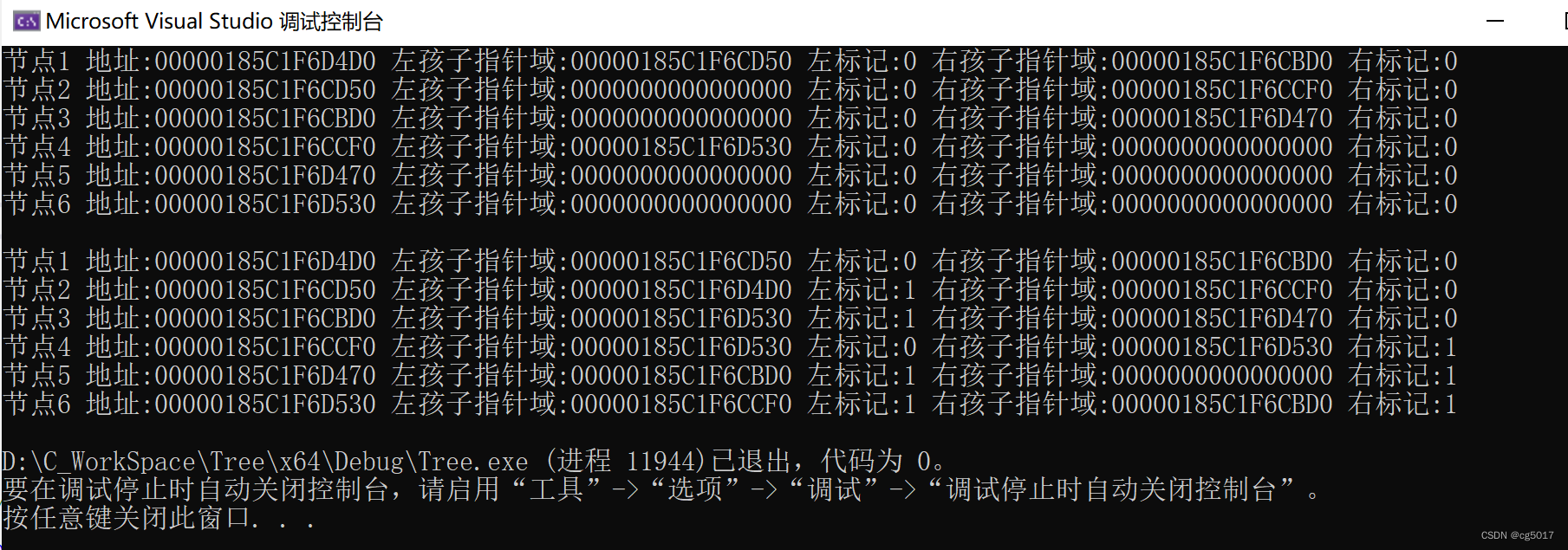
在这里插入图片描述

3.3线索二叉树的遍历

①中序二叉树的遍历

中序二叉树的遍历就不在可以使用之前中序遍历的方式来遍历的，使用方式进行遍历的时候就会出现兜圈子的情况，我们在设计遍历中序线索二叉树的函数时，可以使用以下方法

//中序线索二叉树的遍历
void MidThredOrder(Bitree tree) {if (tree != NULL) {printf("中序线索二叉树遍历如下：\n");BitreeNode* p = tree;p = FirstMidThreadOrderNode(p);   //找到最先开始的左节点while (p != NULL) {	visit(p);      //访问左节点p = NextMidThreadOrderNode(p);    //找到后继节点}printf("\n");}
}

首先通过函数FirstMidThreadOrderNode(p); 找到最先开始遍历的左节点，然后就开始进入循环，不断的通过函数NextMidThreadOrderNode(p); 找到应该访问的后继节点；接下去我们去实现这两个函数

FirstMidThreadOrderNode(p); 

//找到中序线索最先开始的左节点
BitreeNode* FirstMidThreadOrderNode(BitreeNode* p) {assert(p);while (p->LeftTag == 0) {p = p->LeftChild;}return p;
}

NextMidThreadOrderNode(p);

//找到中序线索当前节点的下一个后继节点
BitreeNode* NextMidThreadOrderNode(BitreeNode* p) {assert(p);if (p->RightTag == 0) {  //有右孩子，找右孩子为根节点的树最下方的左节点p = FirstMidThreadOrderNode(p->RightChild);}else {    //左标记为1，就是后继return p->RightChild;}
}

test.cpp

#include"Tree.h"int main() {Bitree tree;IniateBitree(tree,1);InertBitreeNode(tree, 2, 0);  //根节点左孩子插3InertBitreeNode(tree, 3, 1);  //根节点左孩子插3InertBitreeNode(tree->LeftChild, 4, 1);InertBitreeNode(tree->RightChild, 5, 1);InertBitreeNode(tree->LeftChild->RightChild, 6, 0);//层序遍历//LayerOrder(tree);//printf("\n");//中序遍历二叉树printf("中序遍历二叉树如下：\n");MidOrder(tree);//构建中序线索二叉树CreateMidThread(tree);//中序线索二叉树遍历MidThredOrder(tree);//visit(tree); //根节点 1           //visit(tree->LeftChild); // 2//visit(tree->RightChild); // 3//visit(tree->LeftChild->RightChild);  //4//visit(tree->RightChild->RightChild); //5//visit(tree->LeftChild->RightChild->LeftChild); //6return 0;
}

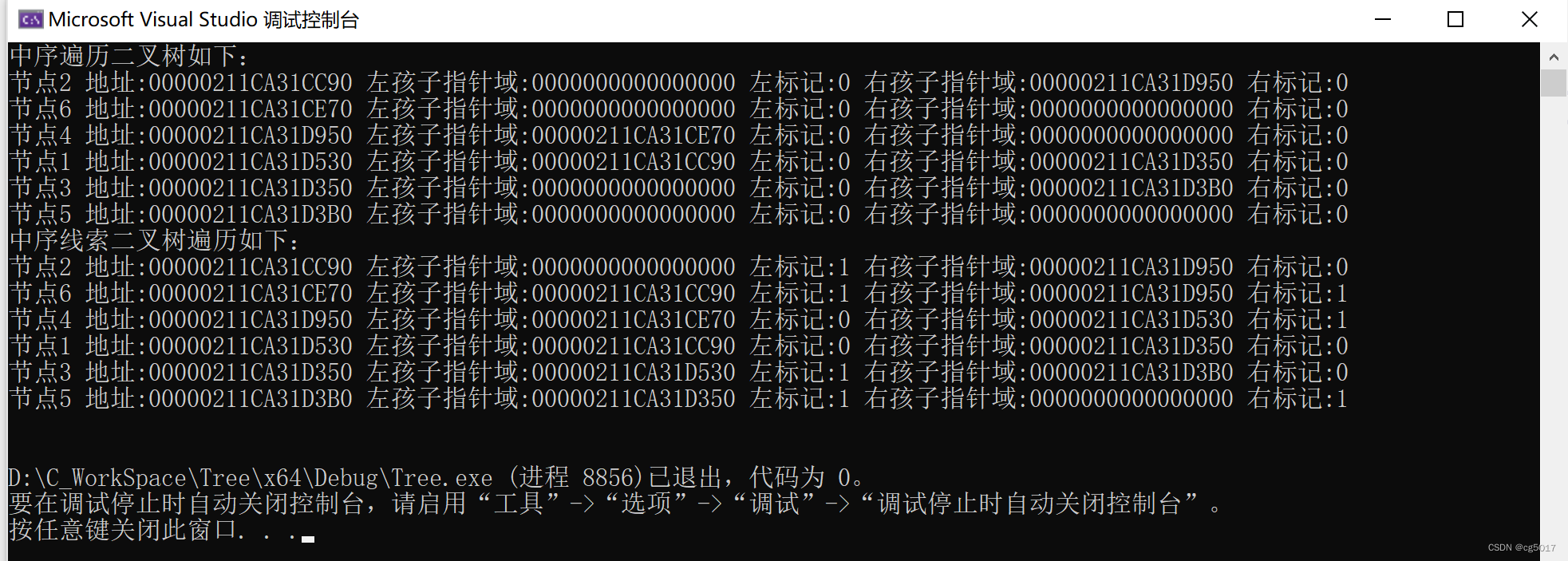
在这里插入图片描述
以上的遍历中序线索二叉树是按着中序遍历顺序的进行的访问的，其实我们也可以按着中序遍历的逆序访问该中序线索二叉树，思想仍然一样，就是先找到最后一个被访问的节点，然后再通过一个函数找前驱节点，然后就这样的依次访问下去。
这里就只给出实现代码，大家可以自己尝试，思想也是非常简单的，对于找最后一个访问的节点，就是只要从根节点出发，该节点的RightTag==0;，就表示它指向的是孩子，继续往下找直到为RightTag==1;，此时就已经是指向被构建线序的节点了，即为找到了最右且最后一个被访问的；对于找前驱节点，就是找以LeftChild为根节点的下一个
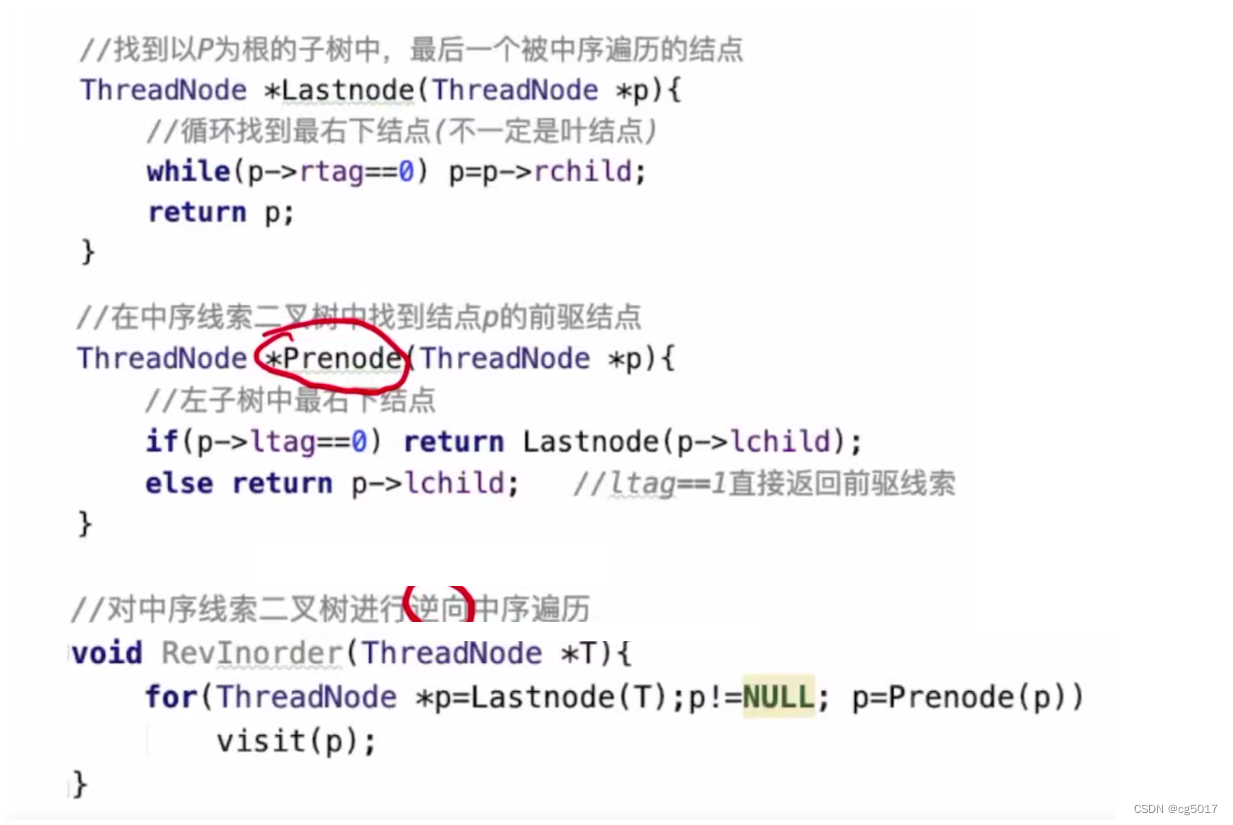
在这里插入图片描述

②先序二叉树的遍历和后序二叉树的遍历

在这里插入图片描述


http://www.ppmy.cn/server/22987.html

相关文章

VUE3与Uniapp 二 （响应式变量ref）

VUE3与Uniapp 二 （响应式变量ref）

<template><!-- 响应式数据变量是双项绑定 --><view>{{num}}</view><view>{{string}}</view><view>{{arry[2]}}</view><view>{{obj.name}}</view> </template><script setup>// 使用ref定义响应式数据…
阅读更多...
三维点云处理-聚类（上）

三维点云处理-聚类（上）

聚类&#xff08;Cluster&#xff09;是数据处理中常用的一种分析方法&#xff0c;聚类的目标是将相似的数据对象划分到同一个簇中&#xff0c;使得同一簇内的数据对象的相似性尽可能大&#xff0c;而不同簇中的数据对象的差异性也尽可能大。  这里主要是介绍两种比较经典的聚…
阅读更多...
ArcGIS批量寻找图层要素中的空洞

ArcGIS批量寻找图层要素中的空洞

空洞指的是图层中被要素包围所形成的没有被要素覆盖的地方&#xff0c;当图层要素数量非常庞大时&#xff0c;寻找这些空洞就不能一个一个的通过目测去寻找了&#xff0c;需要通过使用工具来实现这一目标。 一、【要素转线】工具 利用【要素转线】工具可以将空洞同图层要素处于…
阅读更多...
[ LeetCode ] 题刷刷(Python)-第66题：加一

[ LeetCode ] 题刷刷(Python)-第66题：加一

题目描述 给定一个由 整数 组成的 非空 数组所表示的非负整数&#xff0c;在该数的基础上加一。 最高位数字存放在数组的首位&#xff0c; 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外&#xff0c;这个整数不会以零开头。 示例 示例 1&#xff1a; 输入&#xf…
阅读更多...
AI电销机器人系统源码部署之：freeswitch安装Linux

AI电销机器人系统源码部署之：freeswitch安装Linux

安装 FreeSWITCH&#xff08;一个开源的电话交换系统&#xff09;通常需要一些步骤&#xff0c;以下是在 Linux 系统上安装 FreeSWITCH 的基本指南&#xff1a; 准备工作&#xff1a; 确保你有一个运行 Linux 的服务器&#xff0c;并且有 root 或者具有 sudo 权限的用户。确保服…
阅读更多...
使用R语言进行简单的因子分析

使用R语言进行简单的因子分析

在本文中&#xff0c;将介绍如何使用R语言进行因子分析&#xff0c;并通过一个示例演示整个过程。因子分析是一种多元统计分析方法&#xff0c;用于探索变量之间的潜在结构和关系。R语言提供了丰富的统计工具和包&#xff0c;使因子分析的实现变得简单而高效。 准备工作 首先…
阅读更多...
传感器在机械自动化中的应用有哪些？

传感器在机械自动化中的应用有哪些？

传感器在机械自动化领域扮演了非常关键的角色&#xff0c;它们是实现高效和精准控制的基础。传感器可以检测和测量机械系统中的各种物理量&#xff0c;如位置、速度、温度、压力等&#xff0c;并将这些物理量转换成电信号&#xff0c;以便控制系统能够进行分析和响应。以下是一…
阅读更多...
蓝桥杯ctf2024 部分wp

蓝桥杯ctf2024 部分wp

数据分析 1. packet 密码破解 1. cc 逆向分析 1. 欢乐时光 XXTEA #include<stdio.h> #include<stdint.h> #define DELTA 0x9e3779b9 #define MX (((z>>5^y<<2)(y>>3^z<<4))^((sum^y)(key[(p&3)^e]^z))) void btea(unsigned int* v…
阅读更多...
最新文章

Copyright @ 2022~2023