聚类（Cluster）是数据处理中常用的一种分析方法，聚类的目标是将相似的数据对象划分到同一个簇中，使得同一簇内的数据对象的相似性尽可能大，而不同簇中的数据对象的差异性也尽可能大。
  这里主要是介绍两种比较经典的聚类算法：k-means和高斯混合模型（Gaussian Mixture Model, GMM）。此外，考虑到上述两种算法都可以看做 Expectation Maximization（EM）算法的具体应用，因此这里也对EM算法做一下简单了解。

1. EM算法

  Expectation Maximization（EM）算法算法是一种迭代优化算法，主要用于估计含有隐变量（latent variables）的概率模型参数。网上有很多写的比较好的介绍和推导文章，这里就不再赘述了，感兴趣的可以搜素了解下，这里仅留下自己在学习过程中参考的两篇资料：

• 人人都懂EM算法
• 期望最大化（EM）算法：从理论到实战全解析

  简单来讲：EM算法可以用来处理一些含隐变量的模型的参数估计问题，比如k-means中，我们希望得到 k 个聚类数据，如果我们已经知道了样本集X中每个点的归属信息，那么很容易对 k 个聚类利用极大似然估计（MLE）方法估计出 k 个聚类的信息；但是现在问题时我们不知道样本集中的每个点的归属问题，那么E-M方法就提供了这样的一个求解方法：期望（E）步骤和最大化（M）步骤。假设给定了初始的 k 个聚类中心，E-step 就是 基于给定的k个聚类信息和样本点信息，计算样本点归属于各个聚类中心的条件概率。M-step 就是基于更新后的点的归属信息，计算新的 k 个聚类的信息。重复迭代E-step和M-step至收敛。

EM-算法流程：

2. K-mean算法

  给定 N 个数据，要求将其划分为 k 个类别。

2.1 基本原理：

1. 初始化：随机给定 k 个初始中心点，即 k 个类别；
2. 分别计算 n 个数据点 x 到 k 个中心点的距离，并将数据点分配给离其最近的中心点，即把 n 个数据点 x 分配到 k 个类别上。
3. 取平均，更新 k 个类别的中心点的位置。
   

数学定义：

1. 给定样本集 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n \} {x1​,x2​,...,xn​}，$x_n\in {\mathbb{R}}^D$
2. 聚类中心 ${\mu }_k,k=1,\mathrm{2...},K$， ${\mu }_k$表示第 k 个聚类的中心
3. 二分变量 r n k ∈ { 0 , 1 } r_{nk} \in \{ 0,1 \} rnk​∈{0,1}， $r_{nk}$表示 当$x_n$属于第 $k_i$个类别时，$r_{nk}=1$，否则为 0
4. 利用损失函数优化目标

$$J=\sum _{n=1}^N\sum _{k=1}^K{r}_{nk}{\Vert x_n-{\mu }_k\Vert }^2$$

5. 重复迭代2-3、4步骤
   

求解函数

• E-step: 固定${\mu }_k$，求解$r_{nk}$

  将 $x_n$ 分配到离其最近的 ${\mu }_k$类别；

• M-step: 固定$r_{nk}$，求解${\mu }_k$
  
    对损失函数 J 求一阶导并令其等于0，即
  
  $$2\sum _{n=1}^N{r}_{nk}(x_n-{\mu }_k)=0,{\mu }_k=\frac{{\sum }_n{r}_{nk}{x}_n}{{\sum }_n{r}_{nk}}$$

• 迭代执行E-step、M-step，直到算法收敛。(判断是否收敛：①${\mu }_k$位置不再变动，或者变化量很小；②$r_{nk}$不再变化；)

工程应用中的一些技巧

1. ${\mu }_k$初始化时应选取样本集中点；
2. 随机初始化多次k-means，选择损失函数 J 最小的作为最终结果；
3. 在E-step中选择 KD-Tree 或 Octree 进行近邻搜索加速；
4. Mini-batch K-Means; 每次迭代选择不同的数据子集进行 E&M；
   

局限性

• k 值未知，需要人为给定；
• 受噪声影响大；
  

2.2 K-mediods K-中心点算法

  由于标准的 K-means 是对每个类别中的所有数据点取均值，因此计算时容易受到 噪声点的影响。
K-mediods法的中心思想：

1. E-step 与 K-means方法相同；
2. 而 M-step 中不是直接对所有数据取均值。对于每个聚类，需要遍历当前类别中的所有数据点，计算$x_n$到其他数据点的距离 S，选取 S 最小的点作为新的 ${\mu }_k$，从而剔除噪声点的影响；

  损失函数 J:

$$J=\sum _{n=1}^N\sum _{k=1}^K{r}_{nk}\nu (X_n,{\mu }_k)$$
  其中：$\nu (X_n,{\mu }_k)$不可导不可取平均。

2.3 K-means算法的应用

1. 图像压缩

  一般图像所占位数为 H x W x 3 (高x宽x通道数)，假设图像有 N 个pixels，每个 pixel 包含 3 个通道信息（RGB），每一位都用0-255之间的数据表示的话，那么所占的存储空间为 24N bits 。如果人为选取 k =2, 3, 10,… (k << N) 中颜色对图像进行表示，会发现将颜色相近的像素用同一种颜色表达时，肉眼对图像内容的差异可能并不敏感，进而通过这种方式表达图像，可以实现图像的数据压缩。

2.4 代码练习

  这里仅记录k-means算法实现的主流程部分：

1. 定义存储聚类所需的结构体

// 定义存储聚类的结构体
typedef struct Cluster{// id, 存储索引, 中心点，unsigned int id;Eigen::VectorXd center;std::vector<int> data_index;int data_index_size;    double delta;Cluster(unsigned int id_):id(id_) {delta = std::numeric_limits<double>::max();data_index_size = 0;}
}Cluster;

2. 聚类中心随机初始化

bool KMeans::init_cluster(int k){// 判断 data_sizesize_t data_size = _data.cols();if(data_size < k){std::cerr << "data_size < k: " << data_size << " : " << k << std::endl;return false;}// 使用当前时间生成随机数来初始化聚类中心srand(int(time(0)));// 为了防止生成的随机数重复，还需要考虑去重逻辑!!!std::set<int> idx_removed;for(int i = 0; i < k;){int idx = rand() % data_size;if(idx_removed.count(idx) != 0){continue;}Cluster cluster(i);cluster.center = _data.col(idx);cluster.data_index.resize(data_size);   // 方便后续添加聚类数据cluster.data_index_size = 0;_clusters.emplace_back(cluster);idx_removed.insert(idx);++i;}print_clusters();return true;
}

3. E-step：计算每个数据点最可能归属的类别

bool KMeans::E_step(){// 不需要聚类时的边界条件！！！if(_clusters.size() <= 0){std::cerr << "clusters size is zero" << std::endl;}// 清除聚类中已分配的数据for(int i = 0; i < _clusters.size(); ++i){_clusters[i].data_index.clear();_clusters[i].data_index_size = 0;}// 计算所有点到这 k 个中心的距离，并分类；for(int i = 0; i < _data.cols(); ++i){// 计算当前点到k个中心的距离，并将其分配给离得最近的中心const Eigen::VectorXd tmp_value = _data.col(i);double distance = std::numeric_limits<double>::max();int id = -1;for(int j = 0; j < _clusters.size(); ++j){Eigen::VectorXd vdiff = tmp_value - _clusters[j].center;double diff = vdiff.norm();if(diff < distance){distance = diff;id = j;}}// 无法分配时，输出点号及错误提示// 否则将其加入到聚类中if(id == -1){std::cerr << "No " << i <<" data can not fine cluster center" << std::endl;return false;}_clusters[id].data_index.emplace_back(i);_clusters[id].data_index_size += 1;}return true;
}

4. M-step: 取平均，更新 k 个类别的中心点的位置

bool KMeans::M_step(){// 需要考虑聚类数量为 0 的情况！！！if(_clusters.size() <= 0){std::cerr << "clusters size is zero" << std::endl;return false;}// 更新聚类for(int i = 0; i < _clusters.size(); ++i){Eigen::VectorXd tmp_value(_clusters[i].center.rows());tmp_value.setZero();for(int j = 0; j < _clusters[i].data_index_size; ++j){tmp_value += _data.col(_clusters[i].data_index[j]);}tmp_value /= _clusters[i].data_index_size;// 更新聚类中心_clusters[i].delta = (tmp_value - _clusters[i].center).norm();_clusters[i].center = tmp_value;}return true;
}

5. 迭代执行E-step、M-step，直到收敛。

bool KMeans::compute(int k, int max_step, double min_update_size){// 检查聚类是否初始化if(!init_cluster(k)){std::cerr << "clusters initial error! " << std::endl;return false;}// 迭代聚类int i = 0;for(i = 0; i < max_step; ++i){// 执行E-stepif(!E_step()){std::cerr << "E_step error! " << std::endl;return false;            }// 执行M-stepif(!M_step()){std::cerr << "M_step error! " << std::endl;return false;               }// 判断是否可以提前结束迭代double update_size = KMeans::get_update_size();if(update_size < min_update_size){std::cout << "stop E-M step, update_size: " << update_size << std::endl;break;}}// 如果达到max_step仍不收敛，输出提示信息if(i >= max_step){std::cout << "reach max_step: " << max_step << std::endl;}return true;
}

3. 高斯混合模型（Gaussian Mixture Model, GMM）

  基本思想：使用高斯分布$N(\mu ,\sigma )$来表示每一个聚类的信息，所有聚类信息结合在一起可以看做是多个高斯分布的线性组合。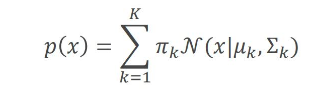

  其中${\pi }_k$表示第 k 个高斯分布所占的权重，${\sum }_{k=1}^K{\pi }_k=1$。

3.2 基本原理

  首先引入一个 K 维的二进制变量$z$：
z k ∈ { 0 , 1 } , Σ k z k = 1 z_k \in \{ 0,1 \}, \space\space \Sigma_k z_k =1 zk​∈{0,1},  Σk​zk​=1
  高斯分布$N({\mu }_k,{\Sigma }_k)$的先验概率$p(z_k=1)$，表示数据点 x 来自第 k 个分布的可能性有多大
$$p(z_k=1)={\pi }_k$$
  给定一个数据点 x，我们希望得到表示聚类“label probability”的条件概率$p(z|x)$，即 x 属于哪一个高斯分布：
$$p(z|x)=\frac{p(x|z)p(z)}{p(x)},p(x)=\sum _{z}p(z)(x|z)$$
  从有向图的角度来看，联合分布$p(x,z)=p(z)p(x|z)$

• $p(z_k=1)={\pi }_k,z=[z_1,\cdots ,z_k,\cdots ,z_K]$，且$0\le {\pi }_k\le 1，{\sum }_{k=1}^K{\pi }_k=1$
• 进一步，$p(z)={\Pi }_{k=1}^K{\pi }_k^{z_k}$
• 那么$p(x|z_k=1)$表示已知第 k 个高斯分布的情况下得到数据点 x 的概率：

$$p(x|z_k=1)=\mathrm{N}(x|{\mu }_k,{\Sigma }_k)$$

• 进一步，$p(x|z)$可以表示为

$$p(x|z)={\Pi }_{k=1}^k\mathrm{N}(x|{\mu }_k,{\Sigma }_k{)}^{z_k}$$
  那么 x 的边缘分布可以通过 $p(x)={\Sigma }_{z}p(x,z)$得到：
$$p(x)=\sum _{z}p(z)p(x|z)=\sum _{k=1}^K{\pi }_k\mathrm{N}(x|{\mu }_k,{\Sigma }_k)$$

推导过程

  假设已知数据点 $x_n$，以及各个高斯分布模型 { π k , μ k , Σ k } \{ \pi_k,\mu_k,\Sigma_k \} {πk​,μk​,Σk​}，求该数据点属于第 k 个高斯分布的概率：
$$p(z|x)=\frac{p(x,z)}{p(x)}=\frac{p(x|z)p(z)}{p(x)}$$
  定义$p(z_k=1|x)$为$\gamma (z_k)$，则：

求解过程

  上一部分是基于高斯模型 { π k , μ k , Σ k } \{ \pi_k,\mu_k,\Sigma_k \} {πk​,μk​,Σk​}给定的情况，但在实际处理中，一般只知道样本数据 $x_n$，需要计算各个高斯模型的参数。也就是要用到极大似然估计（Maximum likelihood），即在给定样本数据点 X 后，如何得到最大可能性的高斯分布模型参数 { π k , μ k , Σ k } \{ \pi_k,\mu_k,\Sigma_k \} {πk​,μk​,Σk​}。
$$p(x)=\sum _{k=1}^K{\pi }_k\mathrm{N}(x|{\mu }_k,{\Sigma }_k)$$
l n p ( X ∣ π , μ , Σ ) = ∑ n = 1 N l n { π k N ( x n ∣ μ k , Σ k ) } ln \space p(X|\pi,\mu,\Sigma)=\sum_{n=1}^{N}ln \{\pi_k \Nu(x_n|\mu_k,\Sigma_k) \} ln p(X∣π,μ,Σ)=n=1∑N​ln{πk​N(xn​∣μk​,Σk​)}

1. 奇点问题

  假设高斯分布的协方差矩阵${\Sigma }_k={\sigma }_k^{2}I$，即每个方向上的方差一致；同时假设有一个数据点 $x_n={\mu }_j$（某个高斯分布的中心）,
$$\mathrm{N}(x_n|x_n,{\sigma }_j^{2}I)=\frac{1}{(2\pi {)}^{1/2}}\frac{1}{{\sigma }_j}$$
  此时如果${\sigma }_j$很小，会导致整体趋于无穷大，此时会出现很大的似然估计。
  解决方法：当出现${\Sigma }_k$很小的情况时，随机初始化成另一个值。

2. 求解 MLE

  GMM的最大似然优化项为：

①固定$\pi$和$\Sigma$，求解${\mu }_k$：（用到了链式求导法则和对数求导）

② 固定 $\pi$和$\mu$，求解${\Sigma }_k$:

③ 固定$\mu$和$\Sigma$，求解 ${\pi }_k$:

总结：

  给定数据集 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n \} {x1​,x2​,...,xn​}，$x_n\in {\mathbb{R}}^D$，和聚类数量 k，如何求解GMM 的极大似然估计？

1. Step-1: 初始化 k 个高斯分布 { π k , μ k , Σ k } \{ \pi_k,\mu_k,\Sigma_k \} {πk​,μk​,Σk​}

2. E-step: 求解一个点属于一个高斯分布的概率$p(z_{nk}=1|x_n)$
   

3. M-step: 利用MLE估算高斯分布模型参数、
   

4. 迭代执行E-step、M-step，直到算法收敛。
   

3.2 代码练习

1. 定义存储聚类结果的结构体
   1. 成员属性：id, pi, mu, sigma. delta
   2. 成员方法：有参构造函数，概率计算函数

typedef struct GMMCluster{// 成员int id;Eigen::VectorXd mu;Eigen::MatrixXd sigma;double pi;double delta;	// 记录聚类中心更新前后的变化量// 方法 double probability(const Eigen::VectorXd& x){// 指数 -1/2 * (x-mu).t * sigma.inverse() * (x-mu)Eigen::VectorXd exp_index = (x - mu).transpose() * sigma.inverse() * (x - mu);exp *= -1. / 2;// 系数double coefficient = 1 / std::pow(2 * M_PI, mu.size() / 2) * 1 / std::pow(sigma.determinant(), 0.5);// 概率值double result = coefficient * exp(exp_index);return result;}GMMCluster(int id_, double pi_): id(id_), pi(pi_){delta = std::numeric_limits<double>::max();}}GMMCluster;

2. 聚类中心初始化

bool init_clusters(int k){// 判断样本集数据是否小于 ksize_t data_size = _data.cols(); // _data为输入数据，大小是dxn，d表示维度，n表示样本数if(data_size < k) {std::cerr << "data_size < k: " << data_size << " : " << k << std::endl;return false;}// 从样本集中随机选取 k 个聚类中srand(int(time(0)));std::set<int> idx_removed;for(int i = 0; i < k;){int idx = rand() % data_size;// 去重if(idx_removed.count(idx) != 0){continue;}GMMCluster cluster(i, 1. / k);cluster.mu = _data.col(idx);cluster.sigma = Eigen::MatrixXd::Identity(_data.rows(), _data.rows());_clusters.emplace_back(cluster); // 不要忘记把已选取的随机点添加到set中！！！idx_removed.insert(idx);++i;}// 初始化Znk矩阵	nxk  n行表示n个样本数据，k列表示每个点归属于当前类别的概率_Z_nk = Eigen::MatrixXd::Zero(_data.cols(), k);return true;
}

2. E-step：求解一个点x_n属于一个类别(高斯分布 k)的概率

// _Z_nk 是一个 nxk的矩阵，每一行表示当前点归属于 k 个高斯分布的概率
// 计算每个点归属于 k 个类别的概率，即 Z_nk 矩阵
bool E_step(){// 遍历每个点，并计算其归属于 k 个类别的概率for(int n = 0; n < _data.cols(); ++n){// 计算当前点在 k 个分布上的总概率double total_prob = 0.;for(int k = 0; k < _Z_nk.cols(); ++k){total_prob += _clusters[k].pi * _clusters[k].probability(_data.col(n));}// 计算更新当前点归属于 k 个分布的概率for(int k = 0; k < _Z_nk.cols(); ++k){double prob = _clusters[k].pi * _clusters[k].probability(_data.col(n));_Z_nk(n, k) = prob / total_prob;}}return true;
}

3. M-step：利用MLE估计高斯分布模型参数

// 利用MLE更新高斯分布模型参数（pi, mu, sigma）
bool M_step(){// 需要用到 N_k, 表示指定分布k时，所有点在该分布上的概率加和Eigen::VectorXd Z_nk_sum = _Z_nk.colwise().sum();// 更新 k 个分布的参数for(size_t k = 0; k < _clusters.size(); ++k){double N_k = Z_nk_sum(k);// 更新 muEigen::VectorXd new_mu_ = (_Z_nk.col(k).transpose() * _data.transpose()) / N_k;Eigen::VectorXd new_mu = new_mu_.transpose();// 更新 sigmaEigen::MatrixXd new_sigma = Eigen::MatrixXd::Zero(_data.rows(), _data.rows());for(size_t n = 0; n < _data.cols(); ++n){new_sigma += _Z_nk(n, k) * (_data.col(n) - new_mu) * (_data.col(n) - new_mu).transpose();}new_sigma /= N_k;// 更新 pidouble new_pi = N_k / _data.cols();// 判断是否存在奇点情况if(new_sigma.determinant() > 1e-6){// 正常更新 模型参数_clusters[k].delta = (new_mu - _clusters[k].mu).norm();_clusters[k].mu = new_mu;_clusters[k].sigma = new_sigma;_clusters[k].pi = new_pi;}else{srand(int(time(0)));int idx = rand() % _data.cols();_clusters[k].mu = _data.col(idx);_clusters[k].sigma = Eigen::MatrixXd::Identity(_data.rows(), _data.rows());}}return true;
}

4. 迭代执行E-step、M-step，直到收敛。

bool compute(int k, int max_step=100, double min_update_size=0.01){// 聚类分布初始化if(!init_clusters(k)){std::cerr << "initial cluster failure!" << std::endl;return false;}// 迭代int i = 0;for(i = 0; i < max_step; ++i){std::cout << "Iteration: " << i << std::endl;// E-stepif(!E_step()){std::cerr << "E_step failure!" << std::endl;return false;}// M_stepif(!M_step()){std::cerr << "M_step failure!" << std::endl;return false;}// 判断是否收敛double update_size = get_update_size();if(update_size < min_update_size){std::cout << "update_size < min_update_size: " << update_size << " : " << min_update_size << std::endl;break;}}// 判断是否达到了最大迭代次数if(i >= max_step){std::cout << "reach max_step: " << max_step << std::endl;}return true;
}

  声明：以上公式和图片来自课程上的PPT部分，小部分参考借鉴了其他博主，仅作为学习、交流使用。

参考资料：

1. 点云学习第三周学习（聚类上）
2. 《三维点云处理》学习笔记（3）：聚类
3. 高斯混合模型（GMM）推导及实现
4. 代码参考