一、机器学习基础概念
1. 定义
机器学习(Machine Learning, ML):通过算法让计算机从数据中自动学习规律,并利用学习到的模型进行预测或决策,而无需显式编程。
2. 与编程的区别
| 传统编程 | 机器学习 |
|---|---|
| 输入:规则+数据 → 输出:结果 | 输入:数据+结果 → 输出:规则 |
| 需要人工编写逻辑 | 自动发现数据中的模式 |
3. 核心要素
- 数据:模型学习的原材料(结构化/非结构化)
- 特征(Feature):数据的可量化属性(如房价预测中的面积、地段)
- 标签(Label):监督学习中的目标变量(如房价数值)
- 模型:从数据中学习到的数学函数(如 y = w 1 x 1 + w 2 x 2 + b y = w_1x_1 + w_2x_2 + b y=w1x1+w2x2+b)
- 损失函数:衡量预测值与真实值的差距(如均方误差 MSE)
- 优化算法:调整模型参数以最小化损失(如梯度下降)
二、机器学习分类
1. 按学习方式分类
(1) 监督学习(Supervised Learning)
- 特点:数据包含输入特征和对应标签
- 典型任务:
- 分类(预测离散类别):垃圾邮件识别(二分类)、手写数字识别(多分类)
- 回归(预测连续数值):房价预测、股票走势预测
- 常用算法:
- 线性回归(Linear Regression)
- 支持向量机(SVM)
- 随机森林(Random Forest)
- 神经网络(Neural Networks)
(2) 无监督学习(Unsupervised Learning)
- 特点:数据只有输入特征,无标签
- 典型任务:
- 聚类:客户分群、新闻主题发现
- 降维:可视化高维数据(t-SNE)
- 异常检测:信用卡欺诈识别
- 常用算法:
- K-Means聚类
- 主成分分析(PCA)
- 自编码器(Autoencoder)
(3) 强化学习(Reinforcement Learning, RL)
- 特点:智能体通过与环境交互获得奖励信号学习策略
- 典型应用:AlphaGo、自动驾驶决策
- 核心要素:
- 状态(State)
- 动作(Action)
- 奖励(Reward)
- 策略(Policy)
2. 按模型类型分类
| 类型 | 特点 | 算法示例 |
|---|---|---|
| 参数模型 | 参数数量固定(如线性模型) | 线性回归、逻辑回归 |
| 非参数模型 | 参数数量随数据增长 | KNN、决策树 |
| 判别模型 | 直接学习决策边界 | SVM、神经网络 |
| 生成模型 | 学习数据分布 | 朴素贝叶斯、GAN |
三、机器学习流程
1. 标准工作流
2. 关键步骤详解
(1) 数据预处理
- 缺失值处理:删除/填充(均值、中位数)
- 异常值检测:Z-Score、IQR方法
- 数据标准化:Min-Max缩放、Z-Score标准化
- 类别编码:One-Hot编码、标签编码
(2) 特征工程
- 特征选择:方差阈值、卡方检验
- 特征构造:组合特征(如面积=长×宽)
- 时间序列特征:滑动窗口统计
- 文本特征:TF-IDF、词嵌入
(3) 模型训练
- 数据集划分:训练集(60-80%)、验证集(10-20%)、测试集(10-20%)
- 超参数调优:网格搜索、随机搜索、贝叶斯优化
- 防止过拟合:交叉验证、早停(Early Stopping)
(4) 模型评估
| 任务类型 | 评估指标 |
|---|---|
| 分类 | 准确率、精确率、召回率、F1 Score、ROC-AUC |
| 回归 | MAE、MSE、R² |
| 聚类 | 轮廓系数、Calinski-Harabasz指数 |
四、经典算法原理
1. 线性回归(Linear Regression)
- 核心思想:找到最佳拟合直线 y = w T x + b y = w^Tx + b y=wTx+b
- 损失函数: M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE = \frac{1}{n}\sum_{i=1}^n(y_i - \hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2
- 求解方法:
- 解析解: w = ( X T X ) − 1 X T y w = (X^TX)^{-1}X^Ty w=(XTX)−1XTy (适用于小数据)
- 数值解:梯度下降(大数据场景)
2. 决策树(Decision Tree)
- 分裂准则:
- 信息增益(ID3算法)
- 基尼不纯度(CART算法)
- 剪枝策略:预剪枝(最大深度限制)、后剪枝(代价复杂度剪枝)
3. 随机森林(Random Forest)
- 核心机制:
- Bagging:通过自助采样(Bootstrap)生成多个子数据集
- 特征随机性:每个节点分裂时随机选择部分特征
- 预测方式:分类任务投票,回归任务平均
4. 支持向量机(SVM)
- 最大间隔分类器:寻找使间隔最大的超平面
- 核技巧:通过核函数将数据映射到高维空间(常用RBF核)
- 数学形式: f ( x ) = s i g n ( ∑ i = 1 n α i y i K ( x i , x ) + b ) f(x) = sign(\sum_{i=1}^n \alpha_i y_i K(x_i, x) + b) f(x)=sign(∑i=1nαiyiK(xi,x)+b)
五、实战案例解析
案例1:鸢尾花分类(监督学习)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier# 加载数据
iris = load_iris()
X, y = iris.data, iris.target# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 训练模型
model = RandomForestClassifier(n_estimators=100)
model.fit(X_train, y_train)# 评估
print("准确率:", model.score(X_test, y_test))
案例2:客户分群(无监督学习)
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6)# 聚类分析
kmeans = KMeans(n_clusters=4)
clusters = kmeans.fit_predict(X)# 可视化
plt.scatter(X[:,0], X[:,1], c=clusters, cmap='viridis')
plt.show()

六、挑战与解决方案
| 常见问题 | 解决方法 |
|---|---|
| 数据不平衡 | SMOTE过采样、类别权重调整 |
| 维度灾难 | 特征选择、降维技术(PCA) |
| 过拟合 | L1/L2正则化、Dropout(神经网络) |
| 计算效率低 | 特征哈希、模型量化 |
线性回归算法
以下是线性回归的全面详解,包含基础概念、数学原理、实战应用及进阶技巧,适合零基础学习者系统掌握:
线性回归终极指南
一、核心概念全景图
二、算法深度解析
1. 数学表达形式
-
简单线性回归:
y = w 1 x + b y = w_1x + b y=w1x+b- w₁:斜率(特征权重)
- b:截距(偏置项)
-
多元线性回归:
y = w 1 x 1 + w 2 x 2 + . . . + w n x n + b y = w_1x_1 + w_2x_2 + ... + w_nx_n + b y=w1x1+w2x2+...+wnxn+b- 示例:房价 = 3.5×面积 + 1.2×卧室数 + 20
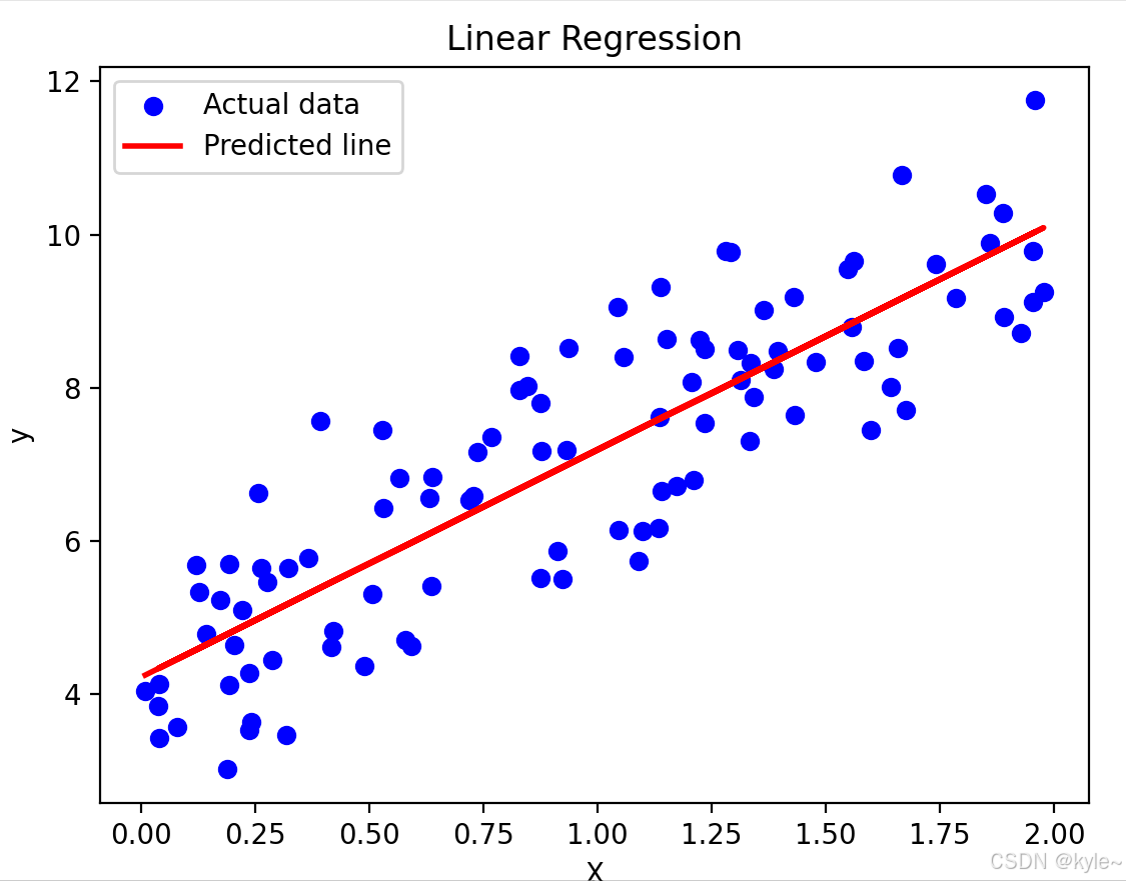
2. 损失函数可视化
均方误差(MSE):
M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2
3. 参数求解
更新规则:
w = w − α ∂ M S E ∂ w w = w - \alpha \frac{\partial MSE}{\partial w} w=w−α∂w∂MSE
b = b − α ∂ M S E ∂ b b = b - \alpha \frac{\partial MSE}{\partial b} b=b−α∂b∂MSE
学习率(α)的影响:
- 太小:收敛慢
- 太大:可能无法收敛
三、实战全流程演练
案例:预测汽车油耗(MPG)
数据集:
| 气缸数 | 排量 | 马力 | 重量 | 油耗 |
|---|---|---|---|---|
| 4 | 2.5 | 120 | 1500 | 28 |
| 6 | 3.0 | 180 | 2000 | 22 |
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split# 加载数据
data = pd.read_csv('auto-mpg.csv')
X = data[['cylinders', 'displacement', 'horsepower', 'weight']]
y = data['mpg']# 数据预处理
X.fillna(X.mean(), inplace=True) # 处理缺失值
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)# 评估模型
print("训练集R²:", model.score(X_train, y_train))
print("测试集R²:", model.score(X_test, y_test))# 预测新数据
new_car = [[4, 2.0, 110, 1400]]
predicted_mpg = model.predict(new_car)
print("预测油耗:", predicted_mpg[0])
关键输出解读:
- 系数权重:
model.coef_显示每个特征的影响程度 - 截距:
model.intercept_表示基础油耗值 - R²分数:0.8表示模型能解释80%的数据变化
四、算法变种与改进
1. 多项式回归
处理非线性关系:
y = w 1 x + w 2 x 2 + b y = w_1x + w_2x^2 + b y=w1x+w2x2+b
from sklearn.preprocessing import PolynomialFeaturespoly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
model.fit(X_poly, y)
2. 正则化回归
| 类型 | 公式 | 特点 |
|---|---|---|
| Ridge回归 | 添加L2正则项: λ ∑ w i 2 \lambda\sum w_i^2 λ∑wi2 | 防止过拟合,保留所有特征 |
| Lasso回归 | 添加L1正则项:$\lambda\sum | w_i |
| ElasticNet | L1+L2组合 | 平衡特征选择与稳定性 |
from sklearn.linear_model import Lassolasso = Lasso(alpha=0.1) # 正则化强度
lasso.fit(X_train, y_train)
五、模型诊断与优化
1. 常见问题诊断表
| 现象 | 可能原因 | 解决方案 |
|---|---|---|
| 训练集R²高,测试集低 | 过拟合 | 增加正则化、减少特征 |
| 所有系数接近零 | 特征尺度差异大 | 数据标准化 |
| 残差不随机分布 | 非线性关系 | 添加多项式特征 |
2. 特征工程技巧
- 分箱处理:将连续年龄分段为青年/中年/老年
- 交互特征:创建面积=长×宽等组合特征
- 离散化:将温度分为低温/常温/高温
3. 超参数调优
from sklearn.model_selection import GridSearchCVparams = {'alpha': [0.001, 0.01, 0.1, 1]}
grid = GridSearchCV(Lasso(), params, cv=5)
grid.fit(X, y)
print("最佳参数:", grid.best_params_)
六、数学推导(简化版)
1. 最小二乘法推导
目标:找到使 ∑ ( y i − w x i − b ) 2 \sum(y_i - wx_i - b)^2 ∑(yi−wxi−b)2最小的w和b
求导过程:
-
对w求导:
∂ ∂ w = − 2 ∑ x i ( y i − w x i − b ) = 0 \frac{\partial}{\partial w} = -2\sum x_i(y_i - wx_i - b) = 0 ∂w∂=−2∑xi(yi−wxi−b)=0 -
对b求导:
∂ ∂ b = − 2 ∑ ( y i − w x i − b ) = 0 \frac{\partial}{\partial b} = -2\sum(y_i - wx_i - b) = 0 ∂b∂=−2∑(yi−wxi−b)=0
解得:
w = n ∑ x i y i − ∑ x i ∑ y i n ∑ x i 2 − ( ∑ x i ) 2 w = \frac{n\sum x_iy_i - \sum x_i \sum y_i}{n\sum x_i^2 - (\sum x_i)^2} w=n∑xi2−(∑xi)2n∑xiyi−∑xi∑yi
b = ∑ y i − w ∑ x i n b = \frac{\sum y_i - w\sum x_i}{n} b=n∑yi−w∑xi
愿得一心人,白头不相离。 —卓文君





