强化学习笔记
主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门.
第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
第四章 值迭代和策略迭代
第五章 强化学习实践—GridWorld
第六章 蒙特卡洛方法
第七章 Robbins-Monro算法
文章目录
- 强化学习笔记
- 一、Robbins-Monro 算法
- 实例
- 二、期望估计
- 三、参考资料
一、Robbins-Monro 算法
随机近似(Stochastic Approximation)是指用于解决寻根或优化问题的一类广泛的随机迭代算法。与许多其他求根算法(如梯度下降法、牛顿法)相比,随机近似的强大之处在于它不需要目标函数的表达式或其导数。Robbins-Monro (RM)算法是随机近似领域的开创性工作,下面介绍RM算法的基本框架:
【RM算法】
设 g : R → R g: \mathbb{R}\to \mathbb{R} g:R→R是一个未知函数,也就是说 g g g的形式未知,但能得到带有噪声的观测值,类似神经网络的黑箱子:
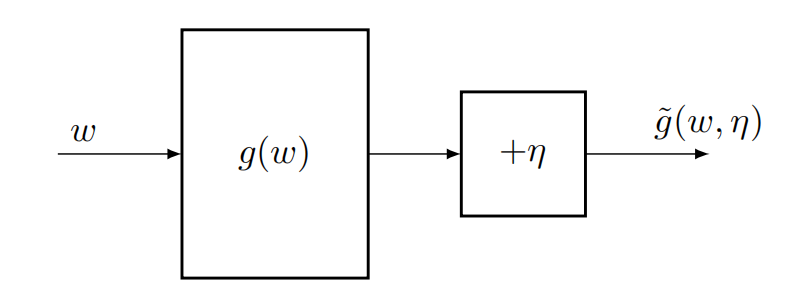
我们想要找到方程 g ( w ) = 0 g(w)=0 g(w)=0的根,RM算法迭代格式如下:
w k + 1 = w k − α k g ~ ( w k , η k ) w_{k+1} = w_k-\alpha_k\tilde{g}(w_k,\eta_k) wk+1=wk−αkg~(wk,ηk)
其中, w k w_k wk是根的第 k k k次迭代的估计值, g ~ ( w k , η k ) \tilde{g}(w_k,\eta_k) g~(wk,ηk)是第 k k k次迭代带有噪声的观测值, α k \alpha_k αk是一个正系数,可以理解为步长.
算法的收敛性由如下定理进行保证:

Note:
- 这个算法要收敛,对函数的要求其实蛮高的,第一个条件要求 g g g的导数为正且不能为+ ∞ \infty ∞,这就是说要求函数是单调递增的;
- 若函数单调递增,我们可以通过下图直观的了解算法是如何通过迭代找到根的,和牛顿法求根的思想很类似只不过牛顿法用到了函数导数的信息,比RM算法的要求更高,RM算法不需要函数导数的信息;

- 如果我们需要求一个优化问题 min f \min f minf,可以转换为 g = ∇ f = 0 g=\nabla f=0 g=∇f=0这样的求根的问题,此时要求 ∇ g > 0 \nabla g>0 ∇g>0,事实上是要求 f f f的海瑟矩阵正定,即要求函数为凸函数,这和很对凸优化算法对函数的要求一样,只有当 f f f为凸函数时,算法才能保证收敛性.
- (b)条件是要求步长为消失步长,常见的消失步长如 a k = 1 k a_k=\frac1k ak=k1.
- (c)条件是对噪声的要求,要求噪声不能太离谱.
实例
下面我们通过RM算法来求 f ( x ) = x 3 − 5 f(x)=x^3-5 f(x)=x3−5的根,来加深一下对RM算法的理解,这里我通过传统方法Newton法和RM算法进行对比,代码如下:
# f(x) = x^3 - 5
def f(x):return x**3 - 5# Robbins-Monro algorithm
def robbins_monro(f, x0, max_iter):w = []w.append(x0)x = x0for i in range(max_iter):x = x - 1 / (i+5) * f(x)# stop if x is close to the rootif np.abs(f(x)) < 1e-6:breakw.append(x)return w# newton's method
def newton(f, x0, max_iter):w = [x0]x = x0for i in range(max_iter):x = x - f(x) / (3 * x**2)# stop if x is close to the rootif np.abs(f(x)) < 1e-6:breakw.append(x)return ww_1 = robbins_monro(f, 1, 1000)
w_2 = newton(f, 1, 1000)# plot the iteration
import matplotlib.pyplot as plt
plt.figure(figsize=(8,5),dpi=150)
plt.plot(w_1)
plt.plot(w_2)
plt.xlabel('iteration')
plt.ylabel('x')
plt.legend(['Robbins-Monro', 'Newton'])
plt.show()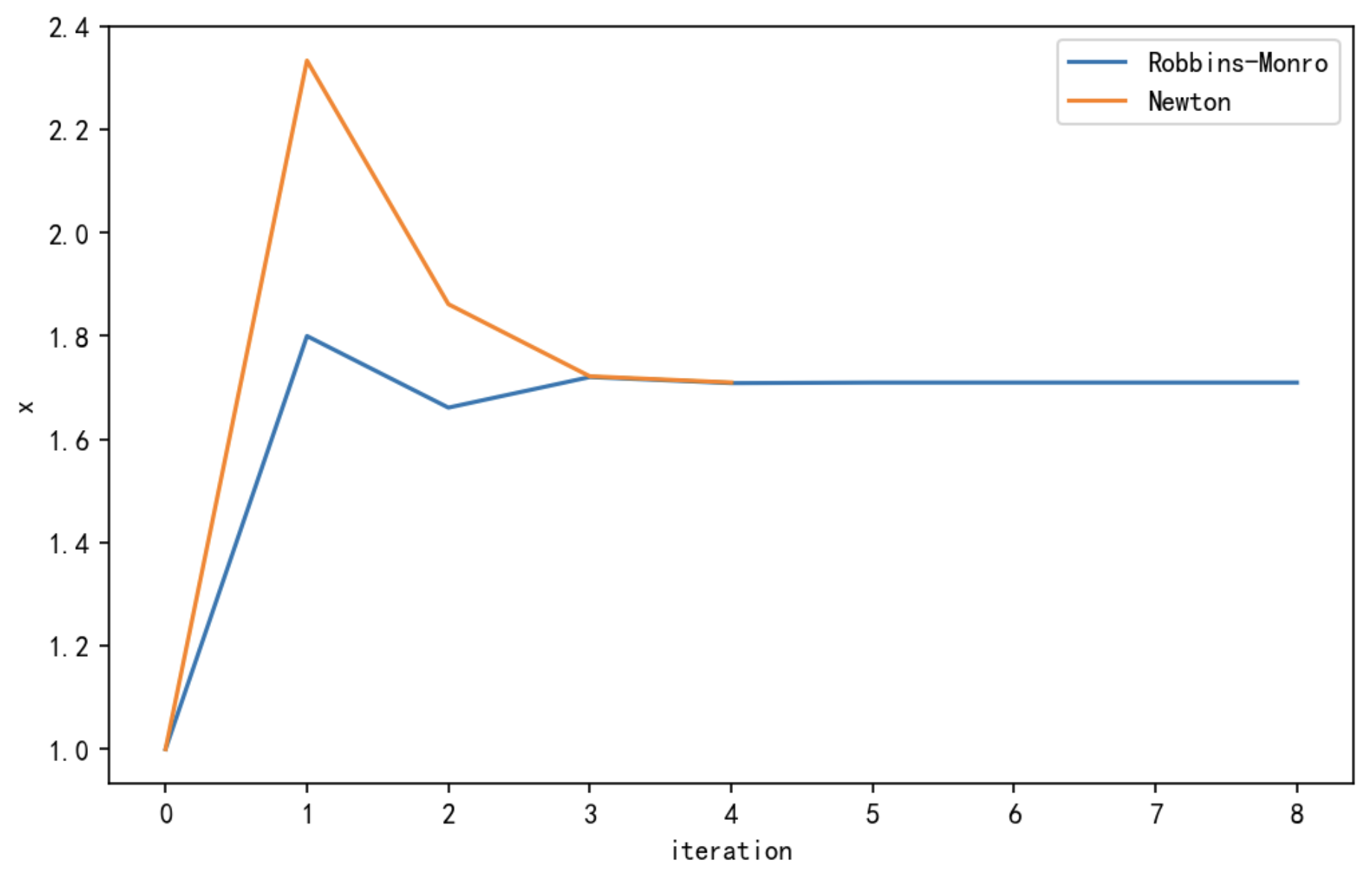
如上图所示,当初值选取合适时,RM算法和Newton算法都能收敛,不过通过选取不同的初值,我们可以发现当初值较远时,RM不会收敛,原因是 f ( x ) = x 3 − 5 f(x)=x^3-5 f(x)=x3−5不满足导数有界的条件,当初值不合适时就容易振荡,算法发散。而牛顿法相对来说就稳定很多,受初值的影响没有那么大,并且收敛速度更快。
二、期望估计
假设有一组样本 x 1 , x 2 , ⋯ , x k x_1,x_2,\cdots,x_k x1,x2,⋯,xk服从同一个分布,我们想要估计这组样本的均值,当然我们首先想到的是:
E [ X ] = x 1 + x 2 + ⋯ + x k k . \mathbb{E}[X] = \frac{x_1+x_2+\cdots+x_k}{k}. E[X]=kx1+x2+⋯+xk.
但是在强化学习的某些算法中,我们不能一次性得到 n n n个样本,每次得到一个采样,那么我们怎么用迭代的算法来估计这个期望呢?我们记
w k = x 1 + x 2 + ⋯ + x k k , w_k=\frac{x_1+x_2+\cdots+x_k}{k}, wk=kx1+x2+⋯+xk,
那么第 k + 1 k+1 k+1次估计值为:
w k + 1 = x 1 + x 2 + ⋯ + x k + x k + 1 k + 1 = x 1 + x 2 + ⋯ + x k k k k + 1 + x k + 1 k + 1 = k k + 1 w k + 1 k + 1 x k + 1 = w k − 1 k + 1 ( w k − x k + 1 ) . ( 1 ) \begin{aligned} w_{k+1} &=\frac{x_1+x_2+\cdots+x_k+x_{k+1}}{k+1}\\ &=\frac{x_1+x_2+\cdots+x_k}{k}\frac{k}{k+1}+\frac{x_{k+1}}{k+1}\\ &=\frac{k}{k+1}w_k+\frac{1}{k+1}x_{k+1}\\ &=w_k-\frac{1}{k+1}(w_k-x_{k+1}). \end{aligned} \qquad\quad(1) wk+1=k+1x1+x2+⋯+xk+xk+1=kx1+x2+⋯+xkk+1k+k+1xk+1=k+1kwk+k+11xk+1=wk−k+11(wk−xk+1).(1)
这样我们就把对均值的估计写成了迭代的形式,每次得到一个新的样本,我们不用对所有样本求和计算了。只需要在上一次的估计值上进行更新就行。
上面这个迭代格式是我们从样本均值的定义出发得到的,下面我们从RM算法出发来推导一下这个迭代格式,考察如下函数
g ( w ) ≐ w − E [ X ] . \begin{aligned}g(w)\doteq w-\mathbb{E}[X].\end{aligned} g(w)≐w−E[X].原始问题是获得 E [ X ] \mathbb{E}[X] E[X]的值,那么我们可以转换为求 g ( w ) = 0 g(w)=0 g(w)=0的根。给定 w w w的值,我们可以获得的噪声观察是 g ~ ≐ w − x \tilde{g}\doteq w-x g~≐w−x,其中 x x x是 X X X的一个样本,注意, g ~ \tilde{g} g~可以写成
g ~ ( w , η ) = w − x = w − x + E [ X ] − E [ X ] = ( w − E [ X ] ) + ( E [ X ] − x ) ≐ g ( w ) + η , \begin{aligned} \tilde{g}(w,\eta)& =w-x \\ &\begin{aligned}=w-x+\mathbb{E}[X]-\mathbb{E}[X]\end{aligned} \\ &=(w-\mathbb{E}[X])+(\mathbb{E}[X]-x)\doteq g(w)+\eta, \end{aligned} g~(w,η)=w−x=w−x+E[X]−E[X]=(w−E[X])+(E[X]−x)≐g(w)+η,所以此问题的RM算法为
w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − x k ) , w_{k+1}=w_{k}-\alpha_{k}\tilde{g}(w_{k},\eta_{k})=w_{k}-\alpha_{k}(w_{k}-x_{k}), wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk),当 α k = 1 k + 1 \alpha_k=\frac{1}{k+1} αk=k+11时,我们就得到同(1)一样的迭代格式了,而且此时可以验证我们构造的函数以及选取的步长,满足收敛性条件,所以当 k → ∞ k\to\infty k→∞时, w k + 1 → E [ X ] w_{k+1}\to\mathbb{E}[X] wk+1→E[X].
三、参考资料
- Zhao, S… Mathematical Foundations of Reinforcement Learning. Springer Nature Press and Tsinghua University Press.