文章目录
- 概要
- 二叉树的概念
- 分类
- 存储
- 遍历
- 前序
- 中序
- 后序
- 小结
概要
简单写下二叉树都有哪些内容,这篇文章要写什么
对一个数据结构,最先入手的都是定义,然后才会有哪些分类,对二叉树这个数据结构来说,遍历很有用。接下来看看。
二叉树的概念
二叉树的相关概念
二叉树是每个节点最多只有两个分支,分别叫“左子树”,“右子树”。一般是父节点>左子树 而且 父节点<右子树。
分类
基础概念有了,看看都有哪些种类
看过基础概念,再来看看都有哪些二叉树。主要有以下几种:
1. 满二叉树
2. 完全二叉树
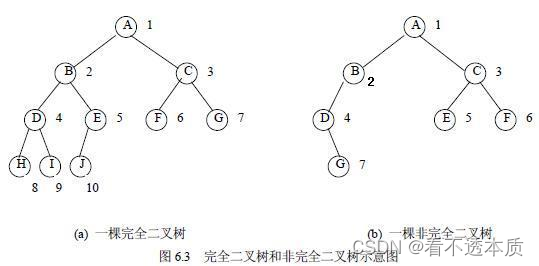
什么是满二叉树呢?在二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫做满二叉树。如下图:
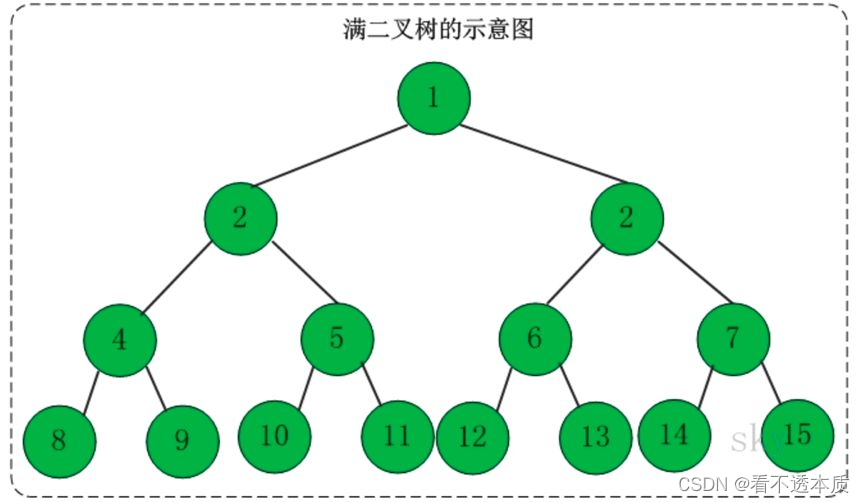
再来看看完全二叉树。在二叉树中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。这样的二叉树是完全二叉树。如下图:
存储
按照存储划分有哪些?
其他的数据结构聊过,都是数组和链表的存储划分。二叉树这么划分,可以分为顺序存储法和链式存储法。
遍历
二叉树的遍历
对于二叉树这种非线性结构,遍历有前序,中序,后序三种遍历方式。
前序
前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
递推公式:
前序遍历的递推公式:
preOrder® = print r->preOrder(r->left)->preOrder(r->right)
void preOrder(Node* root) {if (root == null) return;print root // 此处为伪代码,表示打印root节点preOrder(root->left);preOrder(root->right);
}
中序
中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
中序遍历的递推公式:
inOrder® = inOrder(r->left)->print r->inOrder(r->right)
void inOrder(Node* root) {if (root == null) return;inOrder(root->left);print root // 此处为伪代码,表示打印root节点inOrder(root->right);
}
后序
后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
后序遍历的递推公式:
postOrder® = postOrder(r->left)->postOrder(r->right)->print r
void postOrder(Node* root) {if (root == null) return;postOrder(root->left);postOrder(root->right);print root // 此处为伪代码,表示打印root节点
}
小结
这一篇主要写了二叉树的概念,分类,完全二叉树,满二叉树;按照存储划分顺序存储,链式存储;遍历有三种方式:前序,中序,后序;基本上就这么多了。OK,翻篇。