1. 基本概念
1.1 标量
标量由只有一个元素的张量表示。 所以标量计算与程度开发中的普通变量计算没有差异。
import torchx = torch.tensor(3.0)
y = torch.tensor(2.0)x + y, x * y, x / y, x**y
(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))
1.2 向量
向量泛化自标量,可以被视为标量值组成的列表,相当于把标量从零阶推广到一阶,这些标量值被称为向量的元素。
在深度学习中,使用一维张量表示向量,可以理解为一维数组。
- 使用下标来引用向量的任一元素。
- 向量的长度通常称为向量的维度。
- 可以通过张量的.shape属性访问向量的长度。 形状(shape)列出了张量沿每个轴的长度(维数)。
- 单个向量的默认方向为列向量。
x = torch.arange(4)
x
> tensor([0, 1, 2, 3])
x[3]
> tensor(3)
len(x)
> 4x.shape
> torch.Size([4])
1.3 矩阵
矩阵将向量从一阶推广到二阶,它是一个具有两个轴的张量,数学中采用大写字母表示。
- m行n列组成的矩阵,形状表示为(m, n), 当m=n时,则变为方阵。
A = torch.arange(20).reshape(5, 4)
A
tensor([[ 0, 1, 2, 3],[ 4, 5, 6, 7],[ 8, 9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19]])
当我们交换矩阵的行和列时,结果称为矩阵的转置(transpose)。
A.T
>
tensor([[ 0, 4, 8, 12, 16],[ 1, 5, 9, 13, 17],[ 2, 6, 10, 14, 18],[ 3, 7, 11, 15, 19]])
方阵有一种特殊类型是对称矩阵,特点:对称矩阵的转置是矩阵本身。
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
> tensor([[1, 2, 3],[2, 0, 4],[3, 4, 5]])B == B.T
> tensor([[True, True, True],[True, True, True],[True, True, True]])
1.4 张量
向量是一阶张量,矩阵是二阶张量,但实际上张量可以表示更多阶,n阶矩阵,n个轴,n维数组。
张量在处理图像时特别有用,图像常常以n维数组形式出现, 3个轴分别对应于高度、宽度和颜色通道(channel)轴。
X = torch.arange(24).reshape(2, 3, 4)
X>tensor([[[ 0, 1, 2, 3],[ 4, 5, 6, 7],[ 8, 9, 10, 11]],[[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]]])
1.5 计算基本性质
张量的运算基本是围绕元素进行计算,有以下特性:
- 任何按元素的一元运算都不会改变其操作数的形状。
- 相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
# A
(tensor([[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),# 一元运算: A * 2
tensor([[ 0., 2., 4., 6.],[ 8., 10., 12., 14.],[16., 18., 20., 22.],[24., 26., 28., 30.],[32., 34., 36., 38.]]))
# 二元运算:A * B
tensor([[ 0., 1., 4., 9.],[ 16., 25., 36., 49.],[ 64., 81., 100., 121.],[144., 169., 196., 225.],[256., 289., 324., 361.]])
2. 常见计算
2.1 降维求和
降维主要用于减少数据的维度,从而降低模型的复杂度、减少计算量,并且可以帮助减少过拟合的风险。降维可以使得数据更易于处理和理解,同时可以提高模型的泛化能力。
降维的手段一般是沿着某一个轴求和,从而降低张量的维度。
如前面的二维矩阵A
# 求和前的形状: A, A.shape
(tensor([[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),
(torch.Size([5, 4])
沿着0轴对所有行元素求和,输入轴0的维数在输出形状中消失。
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape> (tensor([40., 45., 50., 55.]), torch.Size([4]))
如果同时给两个轴求和,则二维张量将降为一个元素的标量
A.sum(axis=[0, 1]) # 结果和A.sum()相同
> tensor(190.)
一个与求和相关的量是平均值(mean或average)。 我们通过将总和除以元素总数来计算平均值。
# 这两种计算方式结果相同
A.mean(), A.sum() / A.numel()
> (tensor(9.5000), tensor(9.5000))# 计算平均值的函数也可以沿指定轴降低张量的维度。
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
> (tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))
非降维求和:求和时保持维度不变,通过keepdims选项来指定。
sum_A = A.sum(axis=1, keepdims=True)
sum_A> tensor([[ 6.],[22.],[38.],[54.],[70.]])
2.2 向量点积
定义:相同位置按元素乘积的和,常用于加权求和和加权平均的计算。
给定一组由向量x表示的值, 和一组由w表示的权重,x和w和点积可以表示为(x,w),实际上是用x的转置乘以w来进行计算。
- 一个向量x的平方可以表示为点积(x, x)
- 当w为非负整数且和为1时,x和w的点积可以表示加权平均。
用途1:神经网络的前向传播中,将输入特征向量与权重矩阵进行点积操作,可以得到每个神经元的加权输入,然后通过激活函数进行非线性变换,从而得到神经网络的输出。
用途2:特征提取,通过不同神经元之间的点积操作,网络可以提取出不同层次的特征信息。
计算方法之dot api:
x = torch.arange(4, dtype = torch.float32)
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)#
> (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
计算方法之乘积再求和:
torch.sum(x * y)> tensor(6.)
2.3 矩阵向量积
定义:矩阵(m,n) 和一个向量(len=n)相乘,得到一个新的向量(len=m)。
计算过程的本质:矩阵的每一行与向量进行点积运算,得到新向量的每个元素。
注意:这里的向量要当作列向量来看待。
计算方式(以前面的A矩阵和x向量为例):
A.shape, x.shape, torch.mv(A, x)> (torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))
2.4 矩阵乘法
定义: 矩阵A(m,k) 和矩阵B (k, n)相乘,得到一个新的矩阵(m, n),前提是A矩阵的列数与B矩阵的行数相等。
计算过程的本质:
以前面的A(5, 4) 矩阵为例,新创建一个B(4,3)矩阵, AxB将得到一个(5,3)的新矩阵。
B = torch.ones(4, 3)
torch.mm(A, B)> tensor([[ 6., 6., 6.],[22., 22., 22.],[38., 38., 38.],[54., 54., 54.],[70., 70., 70.]])
2.5 范数
范数通常用于衡量向量的大小,可以帮助控制模型参数的大小以及模型的复杂度。
用途:
- 正则化(Regularization)技术经常使用范数来约束模型的参数,以防止过拟合,提高模型的泛化能力。
- 在损失函数中加入范数项也可以帮助优化算法更好地收敛。
L2范数记作||x||:是向量所有元素平方和的平方根,欧几里得距离就是一个L2范数。
u = torch.tensor([3.0, -4.0])
torch.norm(u) # 用于求L2范数> tensor(5.)
L1范数: 向量元素的绝对值之和。
torch.abs(u).sum()> tensor(7.)
LP范数:用于对矩阵求范数,是矩阵所有元素平方和的平方根。这里以前面的A矩阵为例:
torch.norm(A)> tensor(49.6991)
2.6 余弦夹角
范数配合点积,可以计算两个向量之间的夹角余弦值,公式如下:
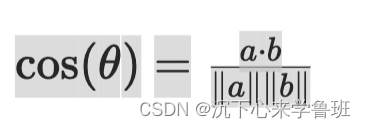
a和b分别是两个向量,a·b表示它们的点积,||a||和||b||分别表示它们的范数(即向量的长度)。通过计算点积和范数,我们可以得到两个向量之间夹角的余弦值,进而推导出它们之间的夹角。
import torch# 定义两个向量
a = torch.tensor([1, 2, 3], dtype=torch.float)
b = torch.tensor([4, 5, 6], dtype=torch.float)# 计算点积
dot_product = torch.dot(a, b)# 计算向量a和b的范数
norm_a = torch.norm(a)
norm_b = torch.norm(b)# 计算夹角余弦值
cosine_similarity = dot_product / (norm_a * norm_b)print("向量a: ", a)
print("向量b: ", b)
print("a和b的点积: ", dot_product)
print("a的范数:", norm_a)
print("b的范数:", norm_b)
print("夹角余弦值: ", cosine_similarity.item())
向量a: tensor([1., 2., 3.])
向量b: tensor([4., 5., 6.])
a和b的点积: tensor(32.)
a的范数: tensor(3.7417)
b的范数: tensor(8.7750)
夹角余弦值: 0.9746317863464355