文章目录
- 1、项目介绍
- 2、导入数据探索工具包
- 3、数据加载
- 4、查看数据集变量信息
- 5、查看数据统计信息
- 6、查看数据字段信息
- 7、箱式图数据探索
- 8、查看数据分布
- 9、特征相关性
- 10、特征筛选
个人主页:道友老李
欢迎加入社区:道友老李的学习社区
【机器学习】实战:天池工业蒸汽量项目(二)特征工程
1、项目介绍
在工业环境中,蒸汽是一种非常常见的能源形式,被广泛应用于各种加热过程、发电以及其它工艺过程中。准确地预测蒸汽的需求量可以帮助企业优化其生产计划,提高能效,减少能源浪费,并降低运营成本。
通常,这样的项目会包含以下几个方面:
- 数据收集:从工业现场的传感器和其他数据源收集历史数据,包括但不限于温度、压力、流量等与蒸汽生成和消耗相关的参数。
- 数据分析:对收集到的数据进行清洗、预处理,并通过统计分析或可视化工具来理解数据的特性。
- 模型建立:使用机器学习算法或者深度学习技术构建预测模型,这些模型能够基于输入的历史数据预测未来的蒸汽需求量。常用的模型可能包括线性回归、随机森林、支持向量机(SVM)、神经网络等。
- 模型评估:通过交叉验证或其他评估方法测试模型的性能,确保模型具有良好的泛化能力,能够在未见过的数据上做出准确的预测。
- 解决方案部署:将训练好的模型部署到实际的工业环境中,实时接收新数据并输出预测结果,帮助工厂实现更高效的能源管理。
- 持续优化:根据模型在真实环境中的表现不断调整和优化,以适应变化的工作条件和技术进步。
火力发电的基本原理是:燃料在燃烧时加热水生成蒸汽,蒸汽压力推动汽轮机旋转,然后汽轮机带动发电机旋转,产生电能。在这一系列的能量转化中,影响发电效率的核心是锅炉的燃烧效率,即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多,包括锅炉的可调参数,如燃烧给量,一二次风,引风,返料风,给水水量;以及锅炉的工况,比如锅炉床温、床压,炉膛温度、压力,过热器的温度等。
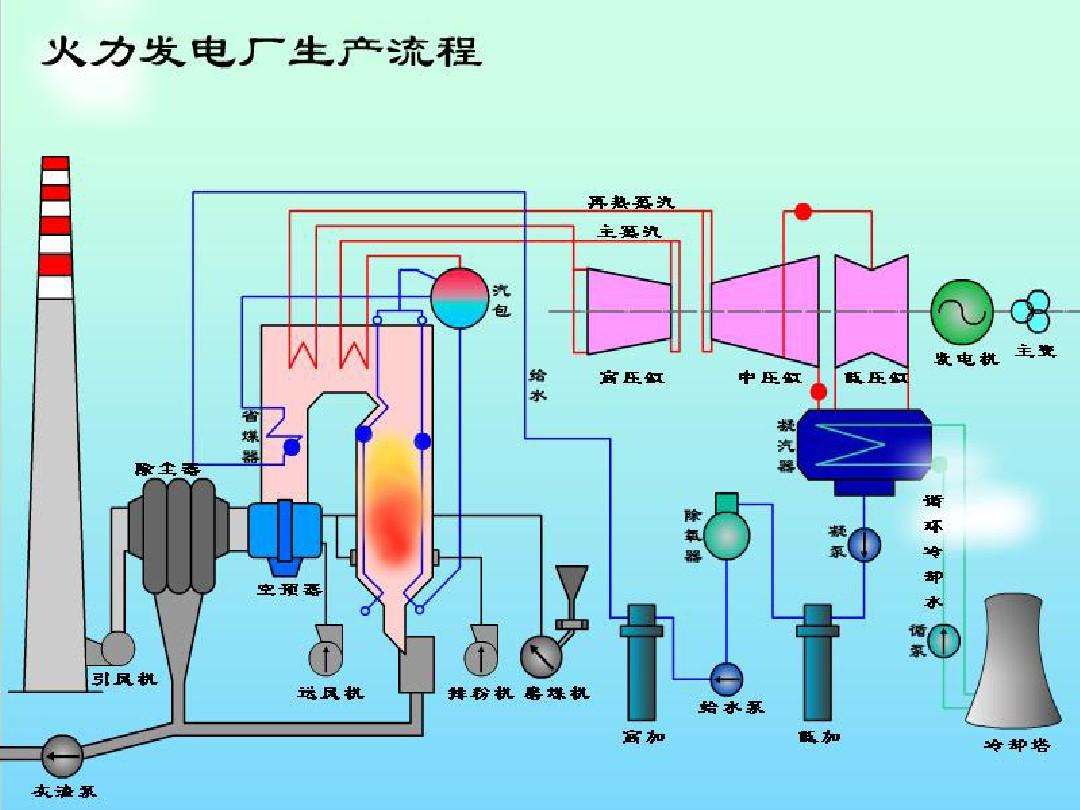
经脱敏后的锅炉传感器采集的数据(采集频率是分钟级别),根据锅炉的工况,预测产生的蒸汽量。
2、导入数据探索工具包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as snsfrom scipy import statsimport warnings
warnings.filterwarnings("ignore")
3、数据加载
train_data_file = "./zhengqi_train.txt"
test_data_file = "./zhengqi_test.txt"train_data = pd.read_csv(train_data_file, sep='\t')
test_data = pd.read_csv(test_data_file, sep='\t')
4、查看数据集变量信息
train_data.info()
test_data.info()
此训练集数据共有2888个样本,数据中有V0-V37共计38个特征变量,变量类型都为数值类型,所有数据特征没有缺失值数据; 数据字段由于采用了脱敏处理,删除了特征数据的具体含义;target字段为标签变量
测试集数据共有1925个样本,数据中有V0-V37共计38个特征变量,变量类型都为数值类型
5、查看数据统计信息
train_data.describe()
上面数据显示了数据的统计信息,例如样本数,数据的均值mean,标准差std,最小值,最大值等
6、查看数据字段信息
train_data.head()
上面显示训练集前5条数据的基本信息,可以看到数据都是浮点型数据,数据都是数值型连续型特征
7、箱式图数据探索
第一个特征箱式图
fig = plt.figure(figsize=(6, 4)) # 指定绘图对象宽度和高度
sns.boxplot(train_data['V0'],orient="v", width=0.5)

全部特征箱式图
# 画箱式图
column = train_data.columns.tolist()[:39] # 列表头
fig = plt.figure(figsize=(20, 40)) # 指定绘图对象宽度和高度
for i in range(38):plt.subplot(13, 3, i + 1) # 13行3列子图sns.boxplot(train_data[column[i]], orient="v", width=0.5) # 箱式图plt.ylabel(column[i], fontsize=8)
plt.show()
8、查看数据分布
对比同一特征变量‘V0’下,训练集数据和测试集数据的分布情况,查看数据分布是否一致
ax = sns.kdeplot(train_data['V0'], color="Red", shade=True)
ax = sns.kdeplot(test_data['V0'], color="Blue", shade=True)
ax.set_xlabel('V0')
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])

查看所有特征变量下,训练集数据和测试集数据的分布情况,分析并寻找出数据分布不一致的特征变量。
dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4*dist_cols,4*dist_rows))i=1
for col in test_data.columns:ax=plt.subplot(dist_rows,dist_cols,i)ax = sns.kdeplot(train_data[col], color="Red", shade=True)ax = sns.kdeplot(test_data[col], color="Blue", shade=True)ax.set_xlabel(col)ax.set_ylabel("Frequency")ax = ax.legend(["train","test"])i+=1
plt.show()
查看特征’V5’, ‘V17’, ‘V28’, ‘V22’, ‘V11’, 'V9’数据的数据分布
col = 3
row = 2
plt.figure(figsize=(5 * col,5 * row))
i=1
for c in ["V5","V9","V11","V17","V22","V28"]:ax = plt.subplot(row,col,i)ax = sns.kdeplot(train_data[c], color="Red", shade=True)ax = sns.kdeplot(test_data[c], color="Blue", shade=True)ax.set_xlabel(c)ax.set_ylabel("Frequency")ax = ax.legend(["train","test"])i+=1

由上图的数据分布可以看到特征’V5’,‘V9’,‘V11’,‘V17’,‘V22’,‘V28’ 训练集数据与测试集数据分布不一致,会导致模型泛化能力差,删除此类特征。
9、特征相关性
特征变量相关性
drop_col_kde = ['V5','V9','V11','V17','V22','V28']
train_data_drop = train_data.drop(drop_col_kde, axis=1)
train_corr = train_data_drop.corr()
train_corr
绘制热力图
# 画出相关性热力图
ax = plt.subplots(figsize=(20, 16))#调整画布大小
# 画热力图 annot=True 显示系数
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True)
半热力图
plt.figure(figsize=(24, 20)) # 指定绘图对象宽度和高度
colnm = train_data_drop.columns.tolist() # 列表头
# 相关系数矩阵,即给出了任意两个变量之间的相关系数
mcorr = train_data_drop.corr()
# 构造与mcorr同维数矩阵 为bool型
mask = np.zeros_like(mcorr, dtype=np.bool)
# 角分线右侧为True
mask[np.triu_indices_from(mask)] = True
# 设置colormap对象,表示颜色
cmap = sns.diverging_palette(220, 10, as_cmap=True)
# 热力图(看两两相似度)
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')

上图为所有特征变量和target变量两两之间的相关系数,由此可以看出各个特征变量V0-V37之间的相关性以及特征变量V0-V37与target的相关性。
10、特征筛选
根据数据分布进行特征删除
# 删除训练数据和预测数据
train_data.drop(drop_col_kde,axis = 1,inplace=True)
test_data.drop(drop_col_kde,axis = 1,inplace= True)
train_data.head()
相关性系数:
- 0.8-1.0 极强相关;
- 0.6-0.8 强相关;
- 0.4-0.6 中等程度相关;
- 0.2-0.4 弱相关;
- 0.0-0.2 极弱相关或无相关(过滤极弱相关的特征)
- 过滤条件特征相关性系数:小于0.1
cond = mcorr['target'].abs() < 0.1
drop_col_corr = mcorr.index[cond]
display(drop_col_corr)
train_data.drop(drop_col_corr,axis = 1,inplace=True)
test_data.drop(drop_col_corr,axis = 1,inplace=True)
display(train_data.head())
数据合并保存
train_data['label'] = 'train'
test_data['label'] = 'test'
all_data = pd.concat([train_data,test_data])
all_data.to_csv('./processed_zhengqi_data.csv',index=False)
all_data.head()





