数据结构C语言描述3(图文结合)--双链表、循环链表、约瑟夫环问题

ops/2024/11/17 14:59:15/

前言

  • 这个专栏将会用纯C实现常用的数据结构和简单的算法；
  • 有C基础即可跟着学习，代码均可运行；
  • 准备考研的也可跟着写，个人感觉，如果时间充裕，手写一遍比看书、刷题管用很多，这也是本人采用纯C语言实现的原因之一；
  • 欢迎收藏 + 关注，本人将会持续更新。

文章目录

双向链表

简介

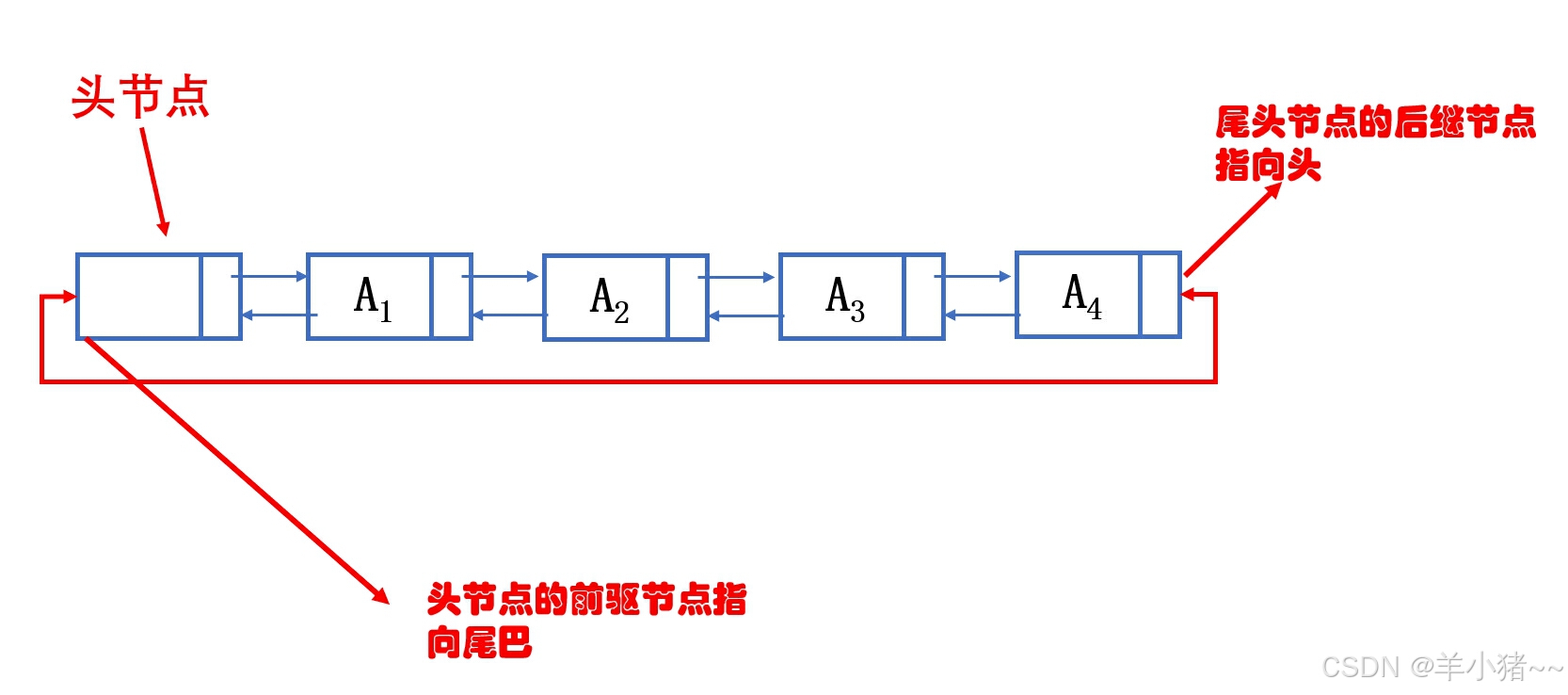
🚡 双向链表，对比单链表来说，顾名思义，就是指向指向有两个指针，指向前后节点。

🌾 结合单链表，单链表有无头和有头之分，双向链表也是一样，这里是无头双链表，采用再封装写法，不是二级指针写法，再封装写法比较写起来比较容易，个人比较偏爱🤠🤠🤠🤠

双链表图示：

在这里插入图片描述

🉑 从ADT抽象中来说：

总结起来一句话：增删改查，🤠🤠🤠，假设双向链表是一个结合，这这个结合功能有：

  • 增加元素
  • 删除元素
  • 拿取元素
  • 查询元素
  • 修改元素
  • …………………………

双链表实现

这里采用再封装的方法，实现无头链表，有头和无头再单链表的那一节以及讲过了，这里采用无头实现

💠 节点封装

在双链表中，对于每一个节点来说，都有一个指向前、指向后节点的指针。

typedef int DataType;typedef struct Node {DataType data;struct Node* prev;  // 前struct Node* next;   // 后
}Node;

⚜️ 链表封装

这一步封装的作用是，可以更好的操作链表的一些操作，这个size的一个再封装写法的核心，无头与有头再实现的过程中，核心就在于第一个头节点的处理，无头如果没有任何节点，则插入的节点则作为第一个节点，但是这样会改变指针的指向，这也是因为需要传递二级指针的原因，而再封装写法则很好的解决了这个问题。

typedef struct List {Node* headNode;Node* tailNode;int size;
}List;

🍨 创建节点

采用calloc创建节点，这样可以自动赋值为0。

Node* create_node(DataType data)
{Node* node = (Node*)calloc(1, sizeof(Node));assert(node);node->data = data;return node;
}

🍤 创建链表

List* create_list()
{List* list = (List*)calloc(1, sizeof(List));assert(list);return list;
}

🤕 插入–头插

  • 情况判断：是否为空链表
    • 空链表：插件节点，作为头
    • 不为空：头插，如图：
void push_front(List* list, DataType data)
{if (list == NULL) {return;}Node* node = create_node(data);if (list->size == 0) {    // 这种写法的优势，不用传递二级指针list->tailNode = node;}else {node->next = list->headNode;list->headNode->prev = node;}list->headNode = node;list->size++;
}

🌮 插入–尾插入

  • 情况判断：是否为空链表
    • 为空：插入，作为头
    • 不为空：找到尾节点，插入
void push_back(List* list, DataType data)
{if (list == NULL) {return;}Node* node = create_node(data);if (list->size == 0) {list->headNode = node;}else {list->tailNode->next = node;node->prev = list->tailNode;}list->tailNode = node;list->size++;
}

💠 插入–任意位置

  • 规则： 在元素后位置插入
  • 情况：3种
    • 没有该元素
    • 尾插
    • 任意插
void insert(List* list, DataType posData, DataType data)
{if (list == NULL || list->size == 0) {  // size ！= 0 保证有头return;}Node* t = list->headNode;while (t->next != NULL && t->data != posData) {t = t->next;}if (t->data != posData) {   // 没有该元素return;}else if (t->next == NULL && t->data == posData) {  // 尾插Node* node = create_node(data);node->prev = t;t->next = node;list->tailNode = node;   // 尾巴移位}else{Node* node = create_node(data);node->next = t->next;t->next->prev = node;node->prev = t;t->next = node;}list->size++;
}

🎧 删除–头删

注意点：释放后指针指向问题：

  • 如果说就一个元素，则删除后，在封装头需要指向NULL
  • 如果不是，则下一个元素的prev指针需要赋值为NULL
void pop_front(List* list)
{if (list == NULL || list->size == 0) {return;}Node* node = list->headNode;list->headNode = node->next;free(node);(list->headNode) ? (list->headNode->prev = NULL) : (list->tailNode = NULL); // 判断是否只有一个节点的情况node = NULL;
}

🚖 删除–尾删除

注意点：释放后指针指向问题：

  • 如果说就一个元素，则删除后，在封装头需要指向NULL
  • 如果不是，则上一个元素的next指针需要赋值为NULL
void pop_back(List* list)
{if (list == NULL || list->size == 0) {return;}Node* node = list->tailNode;list->tailNode = list->tailNode->prev;free(node);(list->tailNode) ? (list->tailNode->next = NULL) : (list->headNode = NULL);list->size--;
}

🦅 删除–任意位置删除

四种情况：

  • 没有找到
  • 找到了
    • 头删
    • 尾删
    • 任意位置删
void erase(List* list, DataType posData)
{if (list == NULL || list->size == 0) {return;}Node* cur = list->headNode;while (cur->next != NULL && cur->data != posData) {cur = cur->next;}// 没有找到if (cur->data != posData) {return;}else if (cur->next == NULL) {   // 尾删除pop_back(list);}else if (cur->prev == NULL) {   // 头删pop_front(list);}else {Node* t = cur;cur->prev->next = cur->next;cur->next->prev = cur->prev;free(t);t = NULL;list->size--;}
}

🌐 万金油函数

bool empty(List* list)
{if (list == NULL) {return true;}return list->size == 0;
}size_t size(List* list)
{if (list == NULL) {return 0;}return list->size;
}

📤 向前遍历

void travel_front(List* list)
{if (list == NULL) {return;}Node* cur = list->headNode;while (cur) {printf("%d ", cur->data);cur = cur->next;}printf("\n");
}

🎉 向后遍历

void travel_back(List* list)
{if (list == NULL) {return;}Node* cur = list->tailNode;while (cur) {printf("%d ", cur->data);cur = cur->prev;}printf("\n");
}

⏰ 总代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>typedef int DataType;typedef struct Node {DataType data;struct Node* prev;struct Node* next;
}Node;typedef struct List {Node* headNode;Node* tailNode;int size;
}List;Node* create_node(DataType data)
{Node* node = (Node*)calloc(1, sizeof(Node));assert(node);node->data = data;return node;
}List* create_list()
{List* list = (List*)calloc(1, sizeof(List));assert(list);return list;
}void push_front(List* list, DataType data)
{if (list == NULL) {return;}Node* node = create_node(data);if (list->size == 0) {list->tailNode = node;}else {node->next = list->headNode;list->headNode->prev = node;}list->headNode = node;list->size++;
}void push_back(List* list, DataType data)
{if (list == NULL) {return;}Node* node = create_node(data);if (list->size == 0) {list->headNode = node;}else {list->tailNode->next = node;node->prev = list->tailNode;}list->tailNode = node;list->size++;
}void insert(List* list, DataType posData, DataType data)
{if (list == NULL || list->size == 0) {  // size ！= 0 保证有头return;}Node* t = list->headNode;while (t->next != NULL && t->data != posData) {t = t->next;}if (t->data != posData) {   // 没有该元素return;}else if (t->next == NULL && t->data == posData) {  // 尾插Node* node = create_node(data);node->prev = t;t->next = node;list->tailNode = node;   // 尾巴移位}else{Node* node = create_node(data);node->next = t->next;t->next->prev = node;node->prev = t;t->next = node;}list->size++;
}void pop_front(List* list)
{if (list == NULL || list->size == 0) {return;}Node* node = list->headNode;list->headNode = node->next;free(node);(list->headNode) ? (list->headNode->prev = NULL) : (list->tailNode = NULL); // 判断是否只有一个节点的情况node = NULL;
}void pop_back(List* list)
{if (list == NULL || list->size == 0) {return;}Node* node = list->tailNode;list->tailNode = list->tailNode->prev;free(node);(list->tailNode) ? (list->tailNode->next = NULL) : (list->headNode = NULL);list->size--;
}void erase(List* list, DataType posData)
{if (list == NULL || list->size == 0) {return;}Node* cur = list->headNode;while (cur->next != NULL && cur->data != posData) {cur = cur->next;}// 没有找到if (cur->data != posData) {return;}else if (cur->next == NULL) {   // 尾删除pop_back(list);}else if (cur->prev == NULL) {   // 头删pop_front(list);}else {Node* t = cur;cur->prev->next = cur->next;cur->next->prev = cur->prev;free(t);t = NULL;list->size--;}
}bool empty(List* list)
{if (list == NULL) {return true;}return list->size == 0;
}size_t size(List* list)
{if (list == NULL) {return 0;}return list->size;
}void travel_front(List* list)
{if (list == NULL) {return;}Node* cur = list->headNode;while (cur) {printf("%d ", cur->data);cur = cur->next;}printf("\n");
}void travel_back(List* list)
{if (list == NULL) {return;}Node* cur = list->tailNode;while (cur) {printf("%d ", cur->data);cur = cur->prev;}printf("\n");
}int main()
{List* list = create_list();for (int i = 1; i < 4; i++) {push_front(list, i);}for (int i = 1; i < 4; i++) {push_back(list, i * 10);}travel_front(list);travel_back(list);insert(list, 3, 33);insert(list, 30, 300);travel_front(list);travel_back(list);pop_front(list);travel_front(list);travel_back(list);pop_back(list);travel_front(list);travel_back(list);erase(list, 33);erase(list, 30);erase(list, 10);travel_front(list);travel_back(list);return 0;
}

循环链表

循环链表分为循环单链表，循环双链表，单链表和双链表又分为有头和无头链表，这里是有头循环双链表。

双向循环链表（Doubly Circular Linked List）是一种数据结构，其中每个节点都包含两个指针，一个指向前一个节点，一个指向后一个节点。与普通链表不同的是，双向循环链表的最后一个节点的下一个指针指向头节点，而头节点的前一个指针指向最后一个节点，形成一个循环。

在这里插入图片描述

🤕 节点封装

typedef int DataType;typedef struct Node {DataType data;struct Node* prev;struct Node* next;
}Node;

🍨 创建节点

Node* create_node(DataType data) 
{Node* node = (Node*)calloc(1, sizeof(Node));assert(node);node->data = data;return node;
}

⚜️ 创建链表

这里需要构建一个循环节点(链表)，如图：

在这里插入图片描述

Node* create_list()
{Node* list = (Node*)calloc(1, sizeof(Node));assert(list);list->next = list;list->prev = list;return list;
}

🎧 插入–头插

双向头删就很容易了，如图：

在这里插入图片描述

void push_front(Node* list, DataType data)
{assert(list);Node* node = create_node(data);node->next = list->next;list->next->prev = node;   // 难点，不用担心 next，prev为空的时候node->prev = list;list->next = node;
}

🌮 插入–尾插

尾巴删除也很容易，因为头和尾巴互相找到，如图：

在这里插入图片描述

void push_back(Node* list, DataType data)
{assert(list);Node* node = create_node(data);node->prev = list->prev;list->prev->next = node;node->next = list;list->prev = node;
}

⛹️‍♀️ 插入–任意位置

任意位置也不难，找到要插入的位置，要注意的是找不到的情况。

// 找到要插入那个节点的位置节点
void insert(Node* list, DataType posData ,DataType data)
{assert(list);Node* cur = list->next;while (cur->next != list && cur->data != posData) {cur = cur->next;}if (cur->data != posData) {   // 思考，为什么不能 cur->next != list ?????return;}else {Node* node = create_node(data);node->next = cur->next;cur->next->prev = node;node->prev = cur;cur->next = node;}}

👟 删除–头删

注意： 一个节点的头节点指向不同。

两种情况：

  1. 如果一个元素，这个时候删除，头节点指向修改和两个元素以上删除不同，这个时候头节点需要指向自己
  2. 两个元素及上
void pop_front(Node* list)
{assert(list);Node* cur = list->next;if (cur == list) {   // 无节点return;}else if(cur->next == list) {   // 一个节点list->prev = list;list->next = list;}else {list->next = cur->next;   // 两个节点以上cur->next->prev = list;}free(cur);cur = NULL;
}

📑 删除–尾删

这个也是简单的，因为可以通过头节点直接找到尾节点，这个时候就只需要一种情况即可，因为创建双链表有一个很好的特性，

void pop_back(Node* list)
{assert(list);Node* cur = list->prev;   // 因为可以获取尾节点if (cur == list) {return;}else {cur->prev->next = list;   // 哪怕是一个节点，也和普通情况也是一样list->prev = cur->prev;   // 这个也是一样，free(cur);cur = NULL;}}

🚴‍♀ 删除–任意位置

很简单，因为这个也不用记录前驱节点，也不用找尾节点了，只需要考虑两种情况：

  1. 没有找到
  2. 找到了
void erase(Node* list, DataType posData)
{assert(list);Node* cur = list->next;while (cur->next != list && cur->data != posData) {cur = cur->next;}if (cur->data != posData) {return;}else {cur->prev->next = cur->next;cur->next->prev = cur->prev;free(cur);cur = NULL;}
}

🔱 遍历

void travel_front(Node* list)
{assert(list);Node* cur = list->next;while (cur != list) {printf("%d ", cur->data);cur = cur->next;}printf("\n");
}void travel_back(Node* list)
{assert(list);Node* cur = list->prev;while (cur != list) {printf("%d ", cur->data);cur = cur->prev;}printf("\n");
}

⚗️ 总代码

#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <stdio.h>// 有头链表实现，简单点typedef int DataType;typedef struct Node {DataType data;struct Node* prev;struct Node* next;
}Node;Node* create_node(DataType data) 
{Node* node = (Node*)calloc(1, sizeof(Node));assert(node);node->data = data;return node;
}Node* create_list()
{Node* list = (Node*)calloc(1, sizeof(Node));assert(list);list->next = list;list->prev = list;return list;
}void push_front(Node* list, DataType data)
{assert(list);Node* node = create_node(data);node->next = list->next;list->next->prev = node;   // 难点，不用担心 next，prev为空的时候node->prev = list;list->next = node;
}void push_back(Node* list, DataType data)
{assert(list);Node* node = create_node(data);node->prev = list->prev;list->prev->next = node;node->next = list;list->prev = node;
}
// 找到要插入那个节点的位置节点
void insert(Node* list, DataType posData ,DataType data)
{assert(list);Node* cur = list->next;while (cur->next != list && cur->data != posData) {cur = cur->next;}if (cur->data != posData) {   // 思考，为什么不能 cur->next != list ?????return;}else {Node* node = create_node(data);node->next = cur->next;cur->next->prev = node;node->prev = cur;cur->next = node;}}void pop_front(Node* list)
{assert(list);Node* cur = list->next;if (cur == list) {return;}else if(cur->next == list) {list->prev = list;list->next = list;}else {list->next = cur->next;cur->next->prev = list;}free(cur);cur = NULL;
}void pop_back(Node* list)
{assert(list);Node* cur = list->prev;if (cur == list) {return;}else {cur->prev->next = list;list->prev = cur->prev;free(cur);cur = NULL;}}void erase(Node* list, DataType posData)
{assert(list);Node* cur = list->next;while (cur->next != list && cur->data != posData) {cur = cur->next;}if (cur->data != posData) {return;}else {cur->prev->next = cur->next;cur->next->prev = cur->prev;free(cur);cur = NULL;}
}void travel_front(Node* list)
{assert(list);Node* cur = list->next;while (cur != list) {printf("%d ", cur->data);cur = cur->next;}printf("\n");
}void travel_back(Node* list)
{assert(list);Node* cur = list->prev;while (cur != list) {printf("%d ", cur->data);cur = cur->prev;}printf("\n");
}int main()
{Node* list = create_list();push_front(list, 1);push_front(list, 2);push_front(list, 3);travel_front(list);travel_back(list);push_back(list, 11);push_back(list, 22);push_back(list, 33);travel_front(list);travel_back(list);insert(list, 2, 20);insert(list, 3, 30);insert(list, 33, 330);travel_front(list);travel_back(list);pop_front(list);travel_front(list);travel_back(list);pop_back(list);travel_front(list);travel_back(list);erase(list, 33);travel_front(list);travel_back(list);return 0;
}

循环链表约瑟夫环问题

讲一个比较有意思的故事：约瑟夫是犹太军队的一个将军，在反抗罗马的起义中，他所率领的军队被击溃，只剩下残余的部队40余人，他们都是宁死不屈的人，所以不愿投降做叛徒。一群人表决说要死，所以用一种策略来先后kill所有人。
于是约瑟夫建议：每次由其他两人一起kill一个人，而被kill的人的先后顺序是由抽签决定的，约瑟夫有预谋地抽到了最后一签，在kill了除了他和剩余那个人之外的最后一人，他劝服了另外一个没死的人投降了罗马。

我们这个规则是这么定的：

  • 在一间房间总共有n个人（下标0～n-1），只能有最后一个人活命。
  • 按照如下规则去排除人：
    • 所有人围成一圈
    • 顺时针报数，每次报到q的人将被排除掉
    • 被排除掉的人将从房间内被移走
    • 然后从被kill掉的下一个人重新报数，继续报q，再清除，直到剩余一人
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>/*
* 用上一个链表，也可以。这里采用无头循环双链表实现
* 无头采用再次封装的写法
*/typedef struct Node {int data;struct Node* prev;struct Node* next;
}Node;typedef struct List {Node* headNode;
}List;// 每一个节点创建都是循环
Node* create_node(int data)
{Node* node = (Node*)calloc(1, sizeof(Node));assert(node);node->data = data;node->prev = node;node->next = node;return node;
}void push_back(List* list, int data)
{assert(list);Node* node = create_node(data);if (list->headNode == NULL) {list->headNode = node;}else {Node* cur = list->headNode->prev;node->next = list->headNode;list->headNode->prev = node;cur->next = node;node->prev = cur;}
}void erase(List* list, Node* node)
{assert(list);assert(node);// 一个节点if (node->next == node) {free(node);node = NULL;list->headNode = NULL;}else {node->prev->next = node->next;node->next->prev = node->prev;if (list->headNode == node) {   // 防止删除头list->headNode = node->next;}free(node);node = NULL;}
}void travel(List* list)
{Node* cur = list->headNode;while (cur->next != list->headNode) {printf("%d ", cur->data);cur = cur->next;}printf("%d ", cur->data);printf("\n");
}// 只做演示，不考虑内存问题
void game_run(int n, int m)
{if (n < 0 || m < 0) {return;}List list = { NULL };for (int i = 1; i <= n; i++) {push_back(&list, i);}travel(&list);Node* cur = list.headNode;while (n > 1) {// 报数for (int i = 1; i < m; i++) {cur = cur->next;}Node* next = cur->next;erase(&list, cur);// 重置报数cur = next;n--;}printf("天选之子: %d\n", cur->data);
}int main()
{game_run(10, 3);return 0;
}

http://www.ppmy.cn/ops/134451.html

相关文章

Qt对话框与界面设计——常见的对话框

Qt对话框与界面设计——常见的对话框

目录 QMessageBox - 提供不同类型的消息对话框 QFileDialog - 文件选择对话框 QColorDialog - 颜色选择对话框 QFontDialog - 字体选择对话框 QInputDialog - 输入对话框 QPrintDialog - 打印机选择对话框 QProgressDialog - 进度对话框 QMessageBox - 异常类型提示 QF…
阅读更多...
IPv6路由基础

IPv6路由基础

前言 IETF组织针对IPv6网络制定了路由协议OSPFv3 OSPFv3 ff02::5是为OSPFv3路由协议预留的IPv6组播地址 OSPFv3中的路由条目下一跳地址时链路本地地址. 运行OSPFv3的路由器使用物理接口的链路本地的单播地址为源地址来发送OSPF报文.相同链路上的路由器互相学习与之相连的其他…
阅读更多...
【3D Slicer】的小白入门使用指南九

【3D Slicer】的小白入门使用指南九

定量医学影像临床研究与实践 任务 定量成像教程 定量成像是从医学影像中提取定量测量的过程。 本教程基于两个定量成像的例子构建： - 形态学：缓慢生长肿瘤中的小体积变化 - 功能：鳞状细胞癌中的代谢活动 第1部分：使用变化跟踪模块测量脑膜瘤的小体积变化第2部分：使用PET标…
阅读更多...
AI 编程编辑器和工具

AI 编程编辑器和工具

以下是几款与 Cursor 类似的 AI 编程编辑器和工具&#xff0c;以及它们的主要特点和差异&#xff1a; 如果你指的是 Cursor 作为一个特定的 AI 编程编辑器&#xff0c;确实我在上一条回答中没有提到它。其实&#xff0c;Cursor 也是一款相对较新的 AI 编程编辑器&#xff0c;它…
阅读更多...
vue3+element-plus==＞ el-form输入响应式失效踩坑!!!!!!!!!!

vue3+element-plus==＞ el-form输入响应式失效踩坑!!!!!!!!!!

坑&#xff1a; 这个坑我是真没想到&#xff0c;找了半天原因... 一开始我是这样写的 <el-form :model"addForm" label-width"100px" ref"addForm"><!-- 表单内容 --> </el-form> 输入框根本输入不了东西&#xff0c;或者…
阅读更多...
GitHub Copilot使用指南：助力开发者加速编程创新

GitHub Copilot使用指南：助力开发者加速编程创新

GitHub Copilot使用指南&#xff1a;助力开发者加速编程创新 简介 1. GitHub Copilot的诞生背景 近年来&#xff0c;AI技术在各行各业迅速发展&#xff0c;尤其是在编程和开发领域&#xff0c;通过自然语言处理和机器学习&#xff0c;AI逐渐能够理解人类的需求和语言。GitHub…
阅读更多...
深入理解Flutter生命周期函数之StatefulWidget(一)

深入理解Flutter生命周期函数之StatefulWidget(一)

目录 前言 1.为什么需要生命周期函数 2.开发过程中常用的生命周期函数 1.initState() 2.didChangeDependencies() 3.build() 4.didUpdateWidget() 5.setState() 6.deactivate() 7.dispose() 3.Flutter生命周期总结 1.调用顺序 2.函数调用时机以及主要作用 4.生…
阅读更多...
微信小程序设置屏幕安全距离

微信小程序设置屏幕安全距离

<script setup> import { onMounted, ref } from vue; let url ref(); onMounted(() > { const windowInfo wx.getWindowInfo(); let safe_left 0; //屏幕左边安全距离 let safe_bottom 0; //屏幕底部安全距…
阅读更多...
最新文章

Copyright @ 2022~2023