目录
- 0 专栏介绍
- 1 引例
- 2 牛顿迭代法
- 3 阻尼牛顿法
- 4 高斯牛顿法
- 5 案例分析与Python实现
- 5.1 牛顿法实现
- 5.2 阻尼牛顿法实现
- 5.3 高斯牛顿法实现
- 5.4 案例分析
0 专栏介绍
🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
🚀详情:运动规划实战进阶:轨迹优化篇
1 引例
给定如图所示的某个函数,如何计算函数零点 x 0 x_0 x0?
在数学上我们如何处理这个问题?
最简单的办法是解方程 f ( x ) = 0 f(x)=0 f(x)=0,在代数学上还有著名的零点判定定理
如果函数 y = f ( x ) y= f(x) y=f(x)在区间 [ a , b ] [a,b] [a,b]上的图象是连续不断的一条曲线,并且有 f ( a ) ⋅ f ( b ) < 0 f(a)·f(b)<0 f(a)⋅f(b)<0,那么函数 y = f ( x ) y= f(x) y=f(x)在区间 ( a , b ) (a,b) (a,b)内有零点,即至少存在一个 c ∈ ( a , b ) c∈(a,b) c∈(a,b),使得 f ( c ) = 0 f(c)=0 f(c)=0,这个 c c c也就是方程 f ( x ) = 0 f(x)= 0 f(x)=0的根。
然而,数学上的方法并不一定适合工程应用,当函数形式复杂,例如出现超越函数形式;非解析形式,例如递推关系时,精确的方程解析一般难以进行,因为代数上还没发展出任意形式的求根公式。而零点判定定理求解效率也较低,需要不停试错。因此,引入今天的主题——牛顿迭代法,服务于工程数值计算。
记第 k k k轮迭代后,自变量更新为 x k x_k xk,令目标函数 f ( x ) f(x) f(x)在 x = x k x=x_k x=xk泰勒展开:
f ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) + o ( x ) f\left( x \right) =f\left( x_k \right) +f'\left( x_k \right) \left( x-x_k \right) +o(x) f(x)=f(xk)+f′(xk)(x−xk)+o(x)
我们希望下一次迭代到根点,忽略泰勒余项,令 f ( x k + 1 ) = 0 f(x_{k+1})=0 f(xk+1)=0,则
x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} xk+1=xk−f′(xk)f(xk)
不断重复运算即可逼近根点。
在几何上,上面过程实际上是在做 f ( x ) f(x) f(x)在 x = x k x=x_k x=xk处的切线,并求切线的零点,在工程上称为局部线性化。如图所示,若 x k x_k xk在 x 0 x_0 x0的左侧,那么下一次迭代方向向右。
若 x k x_k xk在 x 0 x_0 x0的右侧,那么下一次迭代方向向左。
2 牛顿迭代法
记第 k k k轮迭代后,自变量更新为 x k \boldsymbol{x}_k xk,令目标函数 F ( x ) F\left( \boldsymbol{x} \right) F(x)在 x = x k \boldsymbol{x}=\boldsymbol{x}_k x=xk二阶泰勒展开
F ( x ) = F ( x k ) + ∇ T F ( x k ) ( x − x k ) + 1 2 ( x − x k ) T H ( x k ) ( x − x k ) + O ( x ) F\left( \boldsymbol{x} \right) =F\left( \boldsymbol{x}_k \right) +\nabla ^TF\left( \boldsymbol{x}_k \right) \left( \boldsymbol{x}-\boldsymbol{x}_k \right) +\frac{1}{2}\left( \boldsymbol{x}-\boldsymbol{x}_k \right) ^T\boldsymbol{H}\left( \boldsymbol{x}_k \right) \left( \boldsymbol{x}-\boldsymbol{x}_k \right) +O\left( \boldsymbol{x} \right) F(x)=F(xk)+∇TF(xk)(x−xk)+21(x−xk)TH(xk)(x−xk)+O(x)
其一阶梯度为
∇ F ( x ) = ∇ F ( x k ) + H ( x k ) ( x − x k ) \nabla F\left( \boldsymbol{x} \right) =\nabla F\left( \boldsymbol{x}_k \right) +\boldsymbol{H}\left( \boldsymbol{x}_k \right) \left( \boldsymbol{x}-\boldsymbol{x}_k \right) ∇F(x)=∇F(xk)+H(xk)(x−xk)
求 F ( x ) F\left( \boldsymbol{x} \right) F(x)的极小值等价于求 F ′ ( x ) = 0 F'\left( \boldsymbol{x} \right) =0 F′(x)=0的根,根据引例的方法,期望下一次迭代满足 F ′ ( x k + 1 ) = 0 F'\left( \boldsymbol{x}_{k+1} \right) =0 F′(xk+1)=0,则
x k + 1 = x k − H − 1 ( x k ) ∇ F ( x k ) \boldsymbol{x}_{k+1}=\boldsymbol{x}_k-\boldsymbol{H}^{-1}\left( \boldsymbol{x}_k \right) \nabla F\left( \boldsymbol{x}_k \right) xk+1=xk−H−1(xk)∇F(xk)
此即为牛顿法的基本公式,可视为步长为 H − 1 ( x k ) \boldsymbol{H}^{-1}\left( \boldsymbol{x}_k \right) H−1(xk)的自适应梯度下降算法(梯度下降法可以参考数值优化 | 图解梯度下降法与共轭梯度下降法(附案例分析与Python实现))

3 阻尼牛顿法
虽然牛顿法保证收敛,但并非每次迭代都能使函数值下降。设 G ( α ) = F ( x k + α d k ) G\left( \alpha \right) =F\left( \boldsymbol{x}_k+\alpha \boldsymbol{d}_k \right) G(α)=F(xk+αdk),其中 d k = − H − 1 ( x k ) ∇ F ( x k ) \boldsymbol{d}_k=-\boldsymbol{H}^{-1}\left( \boldsymbol{x}_k \right) \nabla F\left( \boldsymbol{x}_k \right) dk=−H−1(xk)∇F(xk),则
G ′ ( α ) = ∇ F ( x k + α d k ) T d k G'\left( \alpha \right) =\nabla F\left( \boldsymbol{x}_k+\alpha \boldsymbol{d}_k \right) ^T\boldsymbol{d}_k G′(α)=∇F(xk+αdk)Tdk
当 H ( x ) \boldsymbol{H}\left( \boldsymbol{x} \right) H(x)正定时有
G ′ ( 0 ) = ∇ F ( x k ) T d k = − ∇ F ( x k ) T H − 1 ( x k ) ∇ F ( x k ) < 0 G'\left( 0 \right) =\nabla F\left( \boldsymbol{x}_k \right) ^T\boldsymbol{d}_k=-\nabla F\left( \boldsymbol{x}_k \right) ^T\boldsymbol{H}^{-1}\left( \boldsymbol{x}_k \right) \nabla F\left( \boldsymbol{x}_k \right) <0 G′(0)=∇F(xk)Tdk=−∇F(xk)TH−1(xk)∇F(xk)<0
根据导数的连续性,必然存在 α > 0 \alpha > 0 α>0使 G ′ ( α ) < 0 G'\left( \alpha \right) <0 G′(α)<0,即
F ( x k + α d k ) < F ( x k ) F\left( \boldsymbol{x}_k+\alpha \boldsymbol{d}_k \right) <F\left( \boldsymbol{x}_k \right) F(xk+αdk)<F(xk)
所以可以在牛顿法的基础上手工进行步长的一维线搜索来保证目标函数下降,称为阻尼牛顿法(Damped Newton’s Method),线搜索的相关理论可以参考数值优化 | 图解线搜索之Armijo、Goldstein、Wolfe准则(附案例分析与Python实现)
4 高斯牛顿法
高斯牛顿法通常用于解决最小二乘问题
min x F ( x ) = 1 2 m min θ ∑ i = 1 m ∥ f i ( x ) ∥ 2 2 = 1 2 m min θ f T ( x ) f ( x ) \min _{\boldsymbol{x}}F\left( \boldsymbol{x} \right) =\frac{1}{2m}\min _{\boldsymbol{\theta }}\sum_{i=1}^m{\left\| f_i\left( \boldsymbol{x} \right) \right\| _{2}^{2}}=\frac{1}{2m}\min _{\boldsymbol{\theta }}\boldsymbol{f}^T\left( \boldsymbol{x} \right) \boldsymbol{f}\left( \boldsymbol{x} \right) xminF(x)=2m1θmini=1∑m∥fi(x)∥22=2m1θminfT(x)f(x)
其中 f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋯ f m ( x ) ] T \boldsymbol{f}\left( \boldsymbol{x} \right) =\left[ \begin{matrix} f_1\left( \boldsymbol{x} \right)& f_2\left( \boldsymbol{x} \right)& \cdots& f_m\left( \boldsymbol{x} \right)\\\end{matrix} \right] ^T f(x)=[f1(x)f2(x)⋯fm(x)]T, f i ( ⋅ ) f_i\left( \cdot \right) fi(⋅)是关于第 i i i个观测样本的目标函数,当 f i ( ⋅ ) f_i\left( \cdot \right) fi(⋅)为线性函数时为线性最小二乘问题,否则是非线性最小二乘问题
考虑一阶泰勒展开 f ( x k + 1 ) = f ( x k ) + J ( x k ) Δ x k \boldsymbol{f}\left( \boldsymbol{x}_{k+1} \right) =\boldsymbol{f}\left( \boldsymbol{x}_k \right) +\boldsymbol{J}\left( \boldsymbol{x}_k \right) \varDelta \boldsymbol{x}_k f(xk+1)=f(xk)+J(xk)Δxk,令
∂ F ( x k + 1 ) ∂ x k + 1 = ∂ ( 1 2 f T ( x k ) f ( x k ) + f T ( x k ) J ( x k ) Δ x k + 1 2 Δ x k T J T ( x k ) J ( x k ) Δ x k ) ∂ x k + 1 = J T ( x k ) f ( x k ) + J T ( x k ) J ( x k ) Δ x k = 0 \begin{aligned}\frac{\partial F\left( \boldsymbol{x}_{k+1} \right)}{\partial \boldsymbol{x}_{k+1}}&=\frac{\partial \left( \frac{1}{2}\boldsymbol{f}^T\left( \boldsymbol{x}_k \right) \boldsymbol{f}\left( \boldsymbol{x}_k \right) +\boldsymbol{f}^T\left( \boldsymbol{x}_k \right) \boldsymbol{J}\left( \boldsymbol{x}_k \right) \varDelta \boldsymbol{x}_k+\frac{1}{2}\varDelta \boldsymbol{x}_{k}^{T}\boldsymbol{J}^T\left( \boldsymbol{x}_k \right) \boldsymbol{J}\left( \boldsymbol{x}_k \right) \varDelta \boldsymbol{x}_k \right)}{\partial \boldsymbol{x}_{k+1}}\\&=\boldsymbol{J}^T\left( \boldsymbol{x}_k \right) \boldsymbol{f}\left( \boldsymbol{x}_k \right) +\boldsymbol{J}^T\left( \boldsymbol{x}_k \right) \boldsymbol{J}\left( \boldsymbol{x}_k \right) \varDelta \boldsymbol{x}_k\\&=0\end{aligned} ∂xk+1∂F(xk+1)=∂xk+1∂(21fT(xk)f(xk)+fT(xk)J(xk)Δxk+21ΔxkTJT(xk)J(xk)Δxk)=JT(xk)f(xk)+JT(xk)J(xk)Δxk=0
从而得到高斯牛顿法应用于最小二乘问题的迭代公式
x k + 1 = x k − ( J T ( x k ) J ( x k ) ) − 1 J T ( x k ) f ( x k ) \boldsymbol{x}_{k+1}=\boldsymbol{x}_k-\left( \boldsymbol{J}^T\left( \boldsymbol{x}_k \right) \boldsymbol{J}\left( \boldsymbol{x}_k \right) \right) ^{-1}\boldsymbol{J}^T\left( \boldsymbol{x}_k \right) \boldsymbol{f}\left( \boldsymbol{x}_k \right) xk+1=xk−(JT(xk)J(xk))−1JT(xk)f(xk)
相当于用一阶梯度信息 J T ( x k ) J ( x k ) \boldsymbol{J}^T\left( \boldsymbol{x}_k \right) \boldsymbol{J}\left( \boldsymbol{x}_k \right) JT(xk)J(xk)来近似二阶的海森矩阵 H ( x ) \boldsymbol{H}\left( \boldsymbol{x} \right) H(x)
5 案例分析与Python实现
5.1 牛顿法实现
核心代码如下所示
class NewtonMethodSolver:def __call__(self, func, g_func, h_func, x0: np.ndarray):x, x_next = x0, Nonetraj = []iteration = 0while iteration < self.max_iters:iteration += 1traj.append(x)gx = g_func(x)if np.sqrt(np.sum(gx ** 2)) < self.eps:breakB = h_func(x)H = np.linalg.inv(B)d = (H @ gx).squeeze()x_next = x - dif math.fabs(func(x) - func(x_next)) < self.eps:breakx = x_nextreturn x, traj
5.2 阻尼牛顿法实现
核心代码如下所示
class DampedNewtonMethodSolver:def __call__(self, func, g_func, h_func, x0: np.ndarray):x, x_next = x0, Nonetraj = []iteration = 0while iteration < self.max_iters:iteration += 1traj.append(x)gx = g_func(x)if np.sqrt(np.sum(gx ** 2)) < self.eps:breakB = h_func(x)H = np.linalg.inv(B)d = (H @ gx).squeeze()alpha = self.line_searcher_.search(func, g_func, x, -d)x_next = x - alpha * dif math.fabs(func(x) - func(x_next)) < self.eps:breakx = x_nextreturn x, traj
5.3 高斯牛顿法实现
核心代码如下所示
class GaussianNewtonSolver:def __call__(self, func, g_func, x0: np.ndarray):x, x_next = x0, Nonem = func(x0).shape[0]traj = []iteration = 0while iteration < self.max_iters:iteration += 1traj.append(x)fx = func(x)gx = g_func(x)d = (np.linalg.inv(gx.T @ gx) @ gx.T @ fx).squeeze()alpha = self.line_searcher_.search(lambda x : func(x).T @ func(x), lambda x : g_func(x).T @ func(x), x, -d)if np.sqrt(np.sum((gx.T @ fx) ** 2)) < self.eps:breakx_next = x - alpha * df_next = func(x_next)if math.fabs(fx.T @ fx - f_next.T @ f_next) / 2.0 / m < self.eps:breakx = x_nextreturn x, traj
5.4 案例分析
以曲线拟合为例展示三种牛顿类优化算法的效果
考虑如下方程:
y = e a x 2 + b x + c + w \boldsymbol{y}=e^{a\boldsymbol{x}^2+b\boldsymbol{x}+c}+\boldsymbol{w} y=eax2+bx+c+w
其中 a a a、 b b b、 c c c是待估计的曲线参数, w \boldsymbol{w} w是高斯噪声,假设有 n n n个观测样本 ( x i , y i ) (x_i,y_i) (xi,yi),希望根据这组样本得到最佳的曲线参数,构造如下的优化问题
F ( θ ) = min 1 2 n ∑ i = 1 n ( y i − e a x i 2 + b x i + c ) 2 F(\boldsymbol{\theta})=\min \frac{1}{2n}\sum_{i=1}^{n}{(y_i-e^{ax_i^2+bx_i+c})^2} F(θ)=min2n1i=1∑n(yi−eaxi2+bxi+c)2
对于牛顿法和阻尼牛顿法来说,是对 F ( θ ) F(\boldsymbol{\theta}) F(θ)整体求导;对于高斯牛顿法来说,则是对
f ( θ ) = [ y 1 − e a x 1 2 + b x 1 + c y 2 − e a x 2 2 + b x 2 + c ⋮ y n − e a x n 2 + b x n + c ] ∈ R n \boldsymbol{f}\left( \boldsymbol{\theta} \right) =\left[ \begin{array}{c} y_1-e^{ax_{1}^{2}+bx_1+c}\\ y_2-e^{ax_{2}^{2}+bx_2+c}\\ \vdots\\ y_n-e^{ax_{n}^{2}+bx_n+c}\\ \end{array} \right] \in \mathbb{R} ^n f(θ)=⎣⎢⎢⎢⎢⎡y1−eax12+bx1+cy2−eax22+bx2+c⋮yn−eaxn2+bxn+c⎦⎥⎥⎥⎥⎤∈Rn
求导
下面来看结果
-
牛顿迭代法
=========================================================== Method: Newton's method Iterations: 12, Using time: 0.032912254333496094 Start Point: [ 2 -1 5] Start Value: 16427.297702943684 End Point: [1.32294736 1.58499573 1.11544194] End Value: 0.4622053698036131 ===========================================================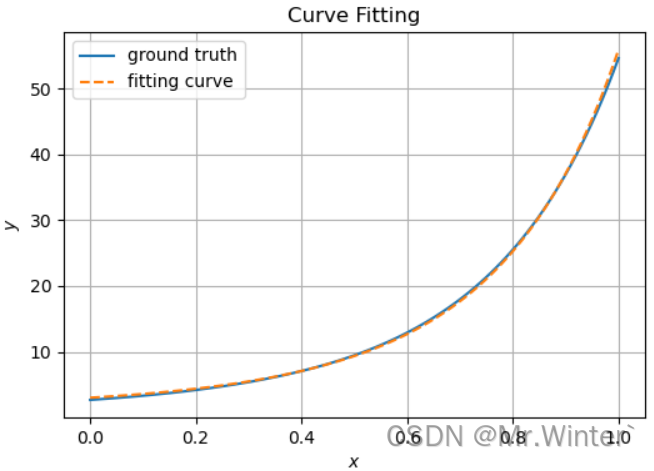
-
阻尼牛顿法
=========================================================== Method: Damped Newton's method Iterations: 10, Using time: 0.2754700183868408 Start Point: [ 2 -1 5] Start Value: 16427.297702943684 End Point: [1.32324891 1.58452748 1.11561685] End Value: 0.46220541076102967 ===========================================================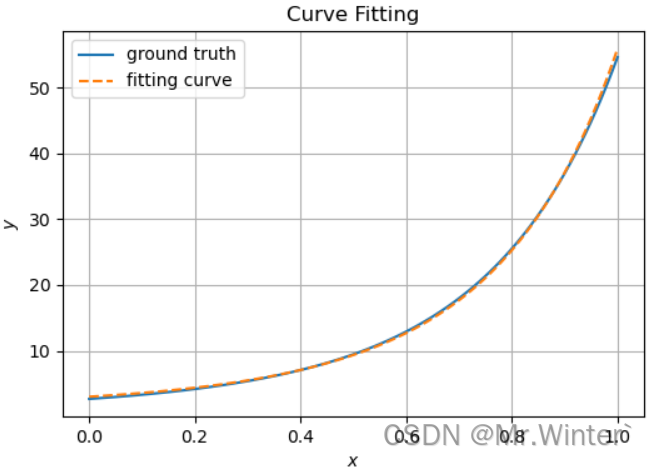
-
高斯牛顿法
=========================================================== Method: Gaussian-Newton Method Iterations: 8, Using time: 0.7493696212768555 Start Point: [ 2 -1 5] Start Value: [[16427.297]] End Point: [1.32328919 1.58446899 1.11562044] End Value: [[0.46220547]] ===========================================================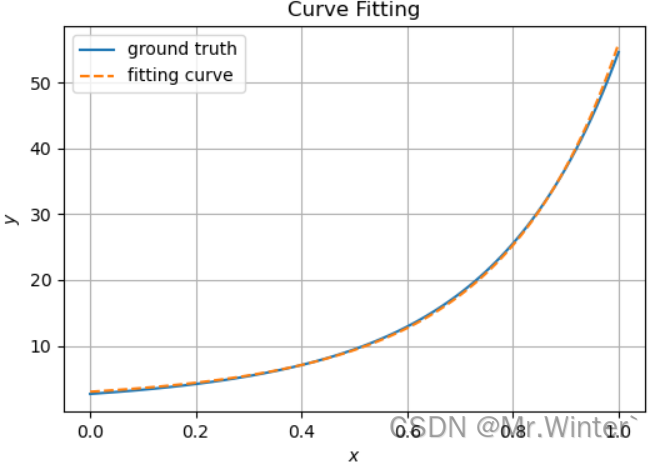
可以看到,在该案例中高斯牛顿法迭代次数最少,牛顿法计算耗时最少
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …