1. 题目描述
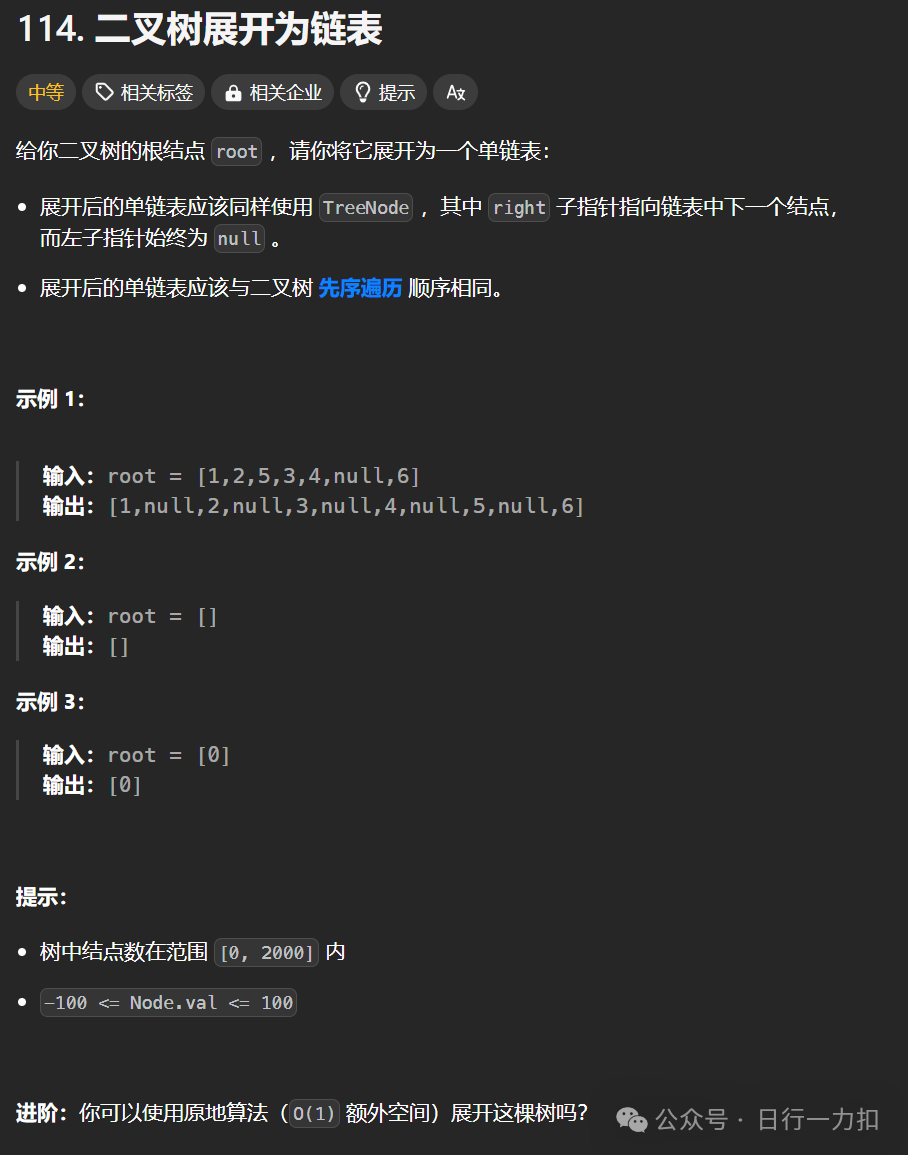
2. 题目分析与解析
2.1 思路一
因为题目中提到:展开后的单链表应该与二叉树 先序遍历 顺序相同,那么我们是不是就可以先先序遍历,然后按照先序遍历的节点一个一个赋值?
其实最简单的思路就是用一个结构按顺序存储所有先序遍历的结果,然后一个一个进行连接,但是这样空间复杂度为O(n),因为这种思路比较简单就不过多赘述了。
我在这里提出的思路是在先序遍历的过程中,进行链表的构建。如果按照这种思路,听起来好像没什么问题,但是如果我进行先序遍历,首先遍历根节点,需要把左节点置空,就会出现下面的情况:
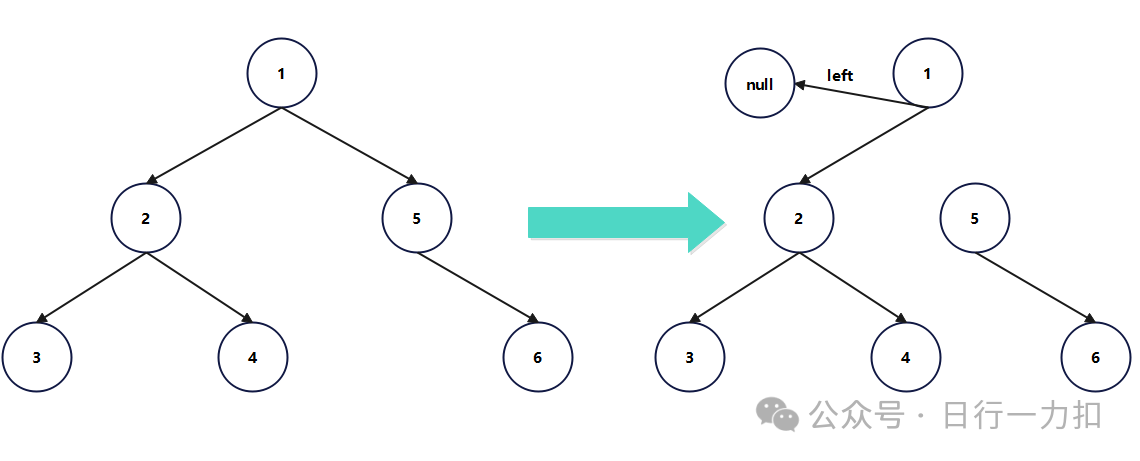
可以看到5,6节点断掉了。所以我们就得用一个结构存储那些断掉的部分,又因为在先序遍历中最先断掉的部分会在遍历过程中也最后被遍历到,所以我们可以使用栈,利用栈的先进后出,存储断掉的部分。这样就有下面的情况:
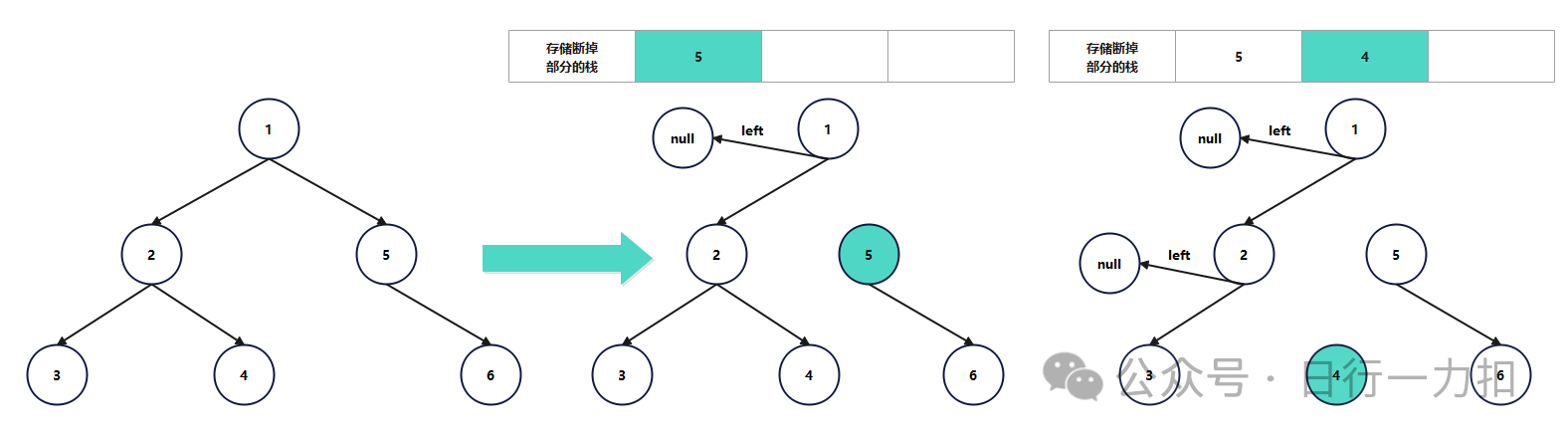
然后这时左边节点发现遍历完毕之后,从栈中取出栈顶4号节点,继续进行上述操作:
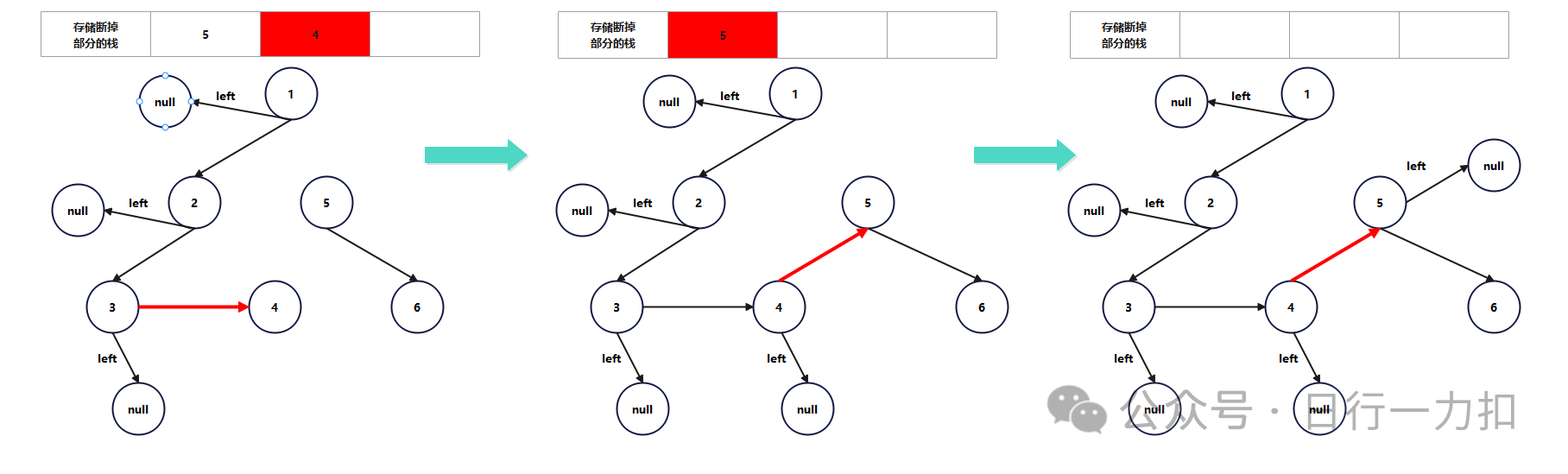
整体思路:
-
按照前序遍历的顺序,用栈存储丢失的右子树节点
-
递归构建左子树的链表
-
从栈中取出节点递归构建右子树的链表
2.2 思路二
参考windliang - 力扣(LeetCode)
因为题目中提到了

那么我们就要想办法把这个栈空间给省略掉,所以我们首先要弄清楚栈到底存的什么东西。其实栈就是不断地存储那些被丢失的右节点。
右节点?既然我们担心右节点丢失,那么我们就可以先把右节点是不是先放在二叉树的某个位置,保存起来,这样就不需要再用栈来额外存储这些右节点了。那到底存储在哪呢?先看一下结果:
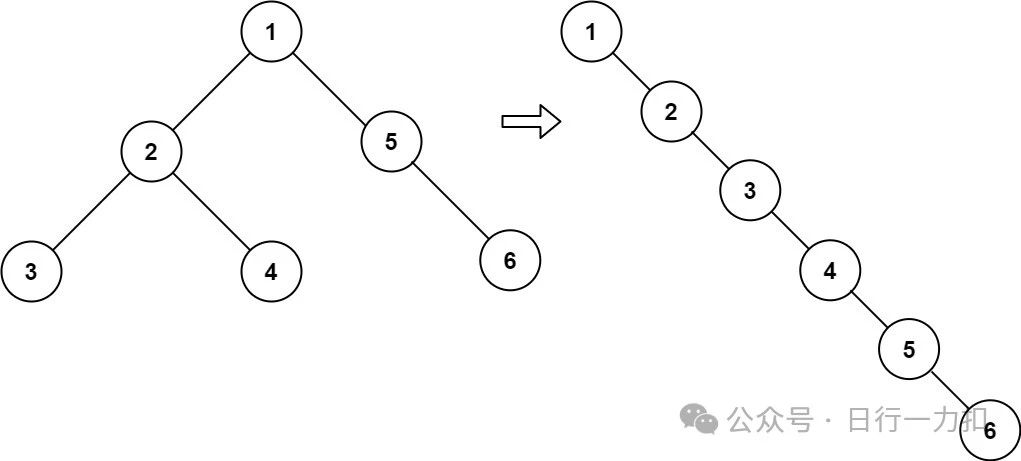
我们可以发现右节点总是在左子树的最右节点的后面,对应上图就是 5在4后面——对应1的左子树最右边一个节点为4,4在3后面——对应2的左子树最右边一个节点为3(因为2的左子树就只有3)。对应图解为:

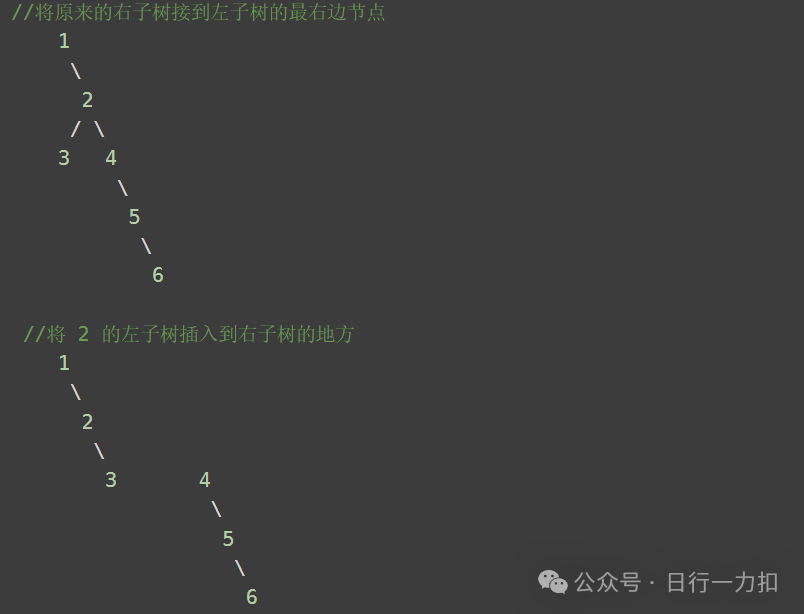

因此我们是不是可以先把右子树存储在左子树最右边一个节点的后面,这样就不需要栈来存储了。现在我们就需要考虑怎么找到左子树的最右边一个节点,然后把右子树接到这个节点后面。之后再看root.right下一个节点,以此类推就可求解。
整体思路:
-
将左子树插入到右子树的地方
-
将原来的右子树接到左子树的最右边节点
-
考虑新的右子树的根节点,一直重复上边的过程,直到新的右子树为 null
2.3 思路三
现在还是抓住问题的本质,我们需要省略掉栈保存的右节点。上面思路二的想法是用左子树的最右节点来临时存储右子树,那么我们可不可以从后往前去遍历,先遍历右子树的部分,然后把这部分的根节点这一个节点存储起来,再遍历左子树,也就是按照后序遍历的变种:右子树->左子树->根节点的方式进行处理。
后序遍历(Postorder Traversal):先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。
具体步骤:
递归地后序遍历左子树。
递归地后序遍历右子树。
访问根节点。
我们依次遍历 6 5 4 3 2 1,然后每遍历一个节点就将当前节点的右指针更新为上一个节点。
遍历到 5,把 5 的右指针指向 6。6 <- 5 4 3 2 1。
遍历到 4,把 4 的右指针指向 5。6 <- 5 <- 4 3 2 1。
按照这样的方式我们只需要一个临时变量存储前序节点就可以了。
3. 代码实现
3.1 思路一
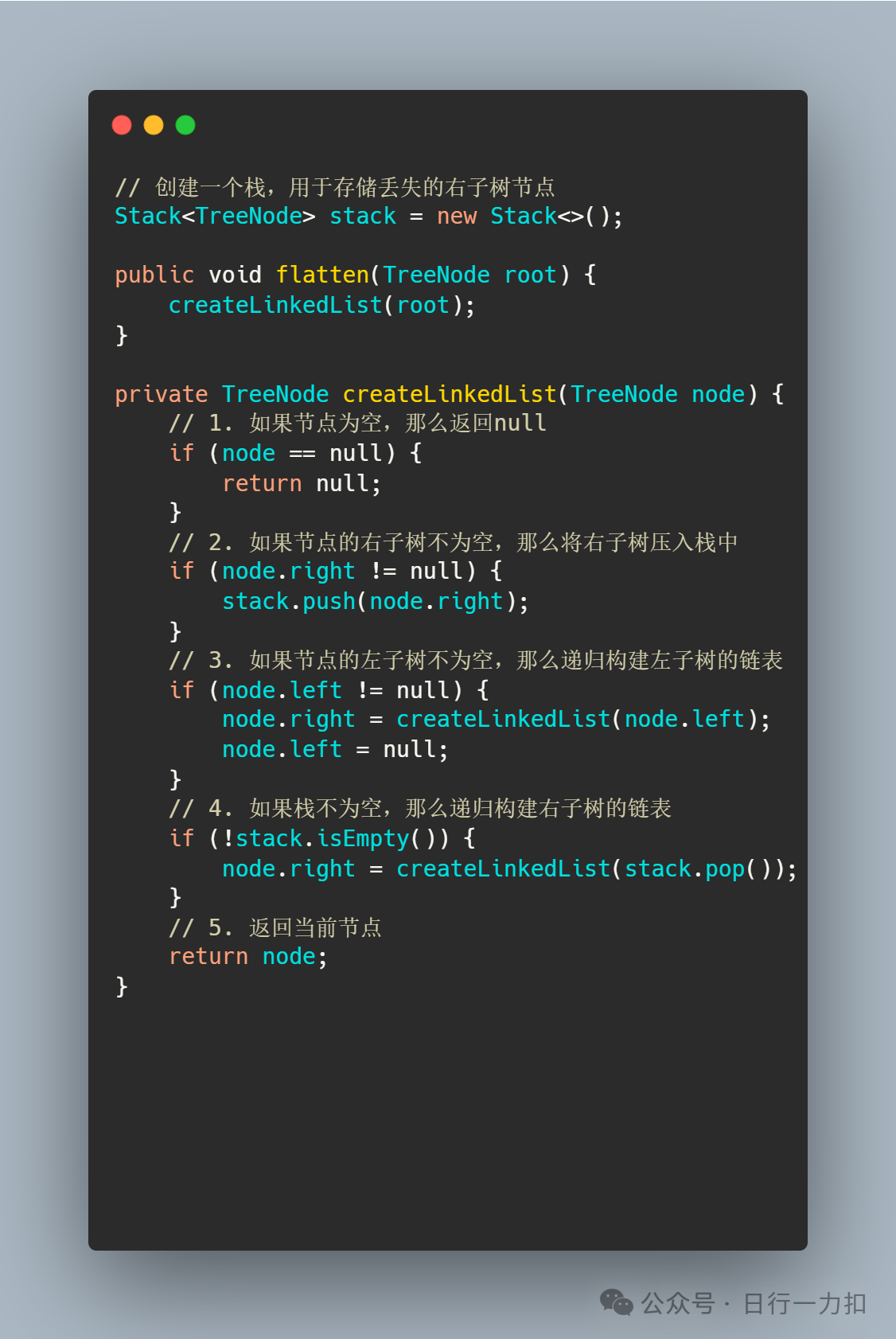
3.2 思路二
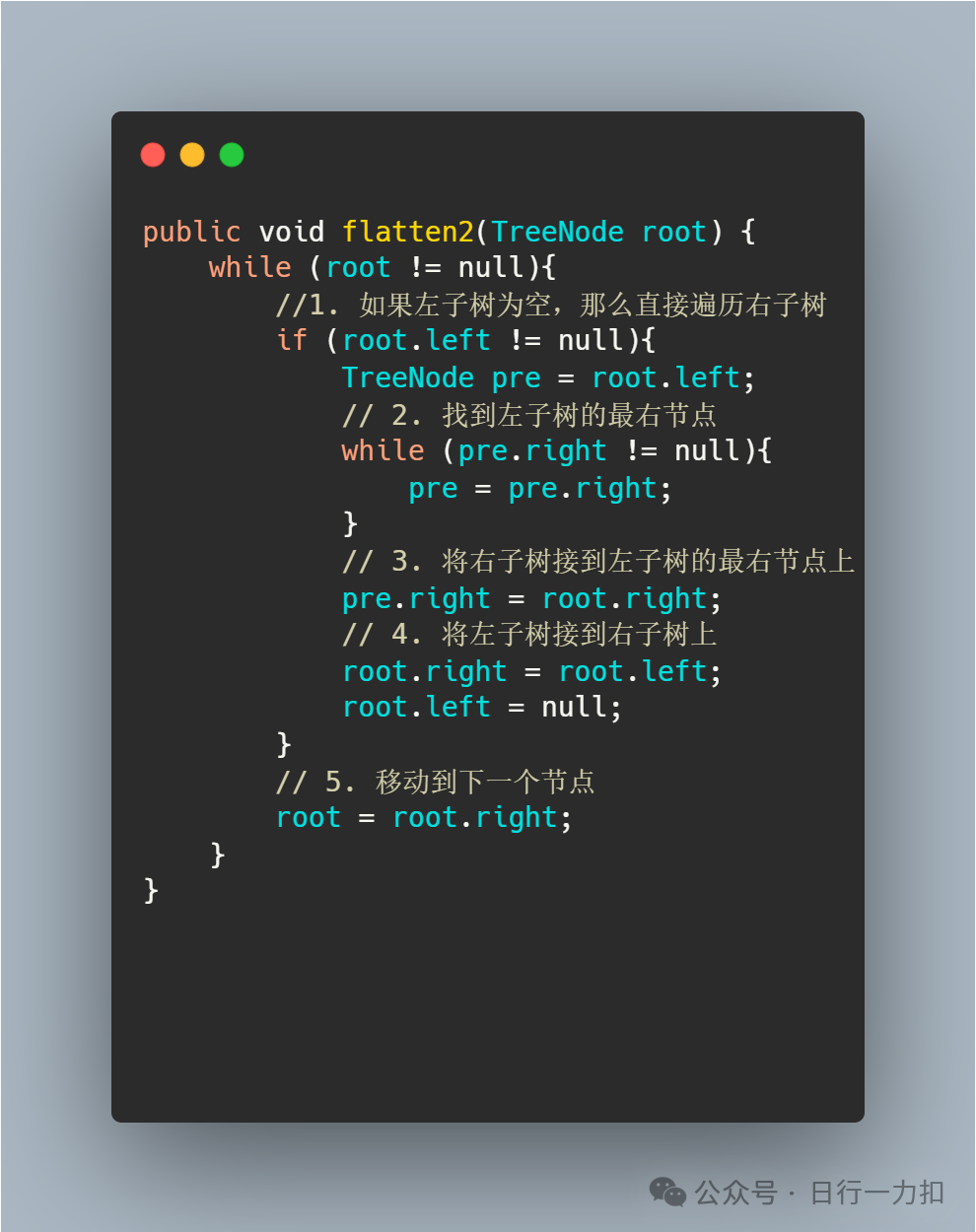
3.3 思路三
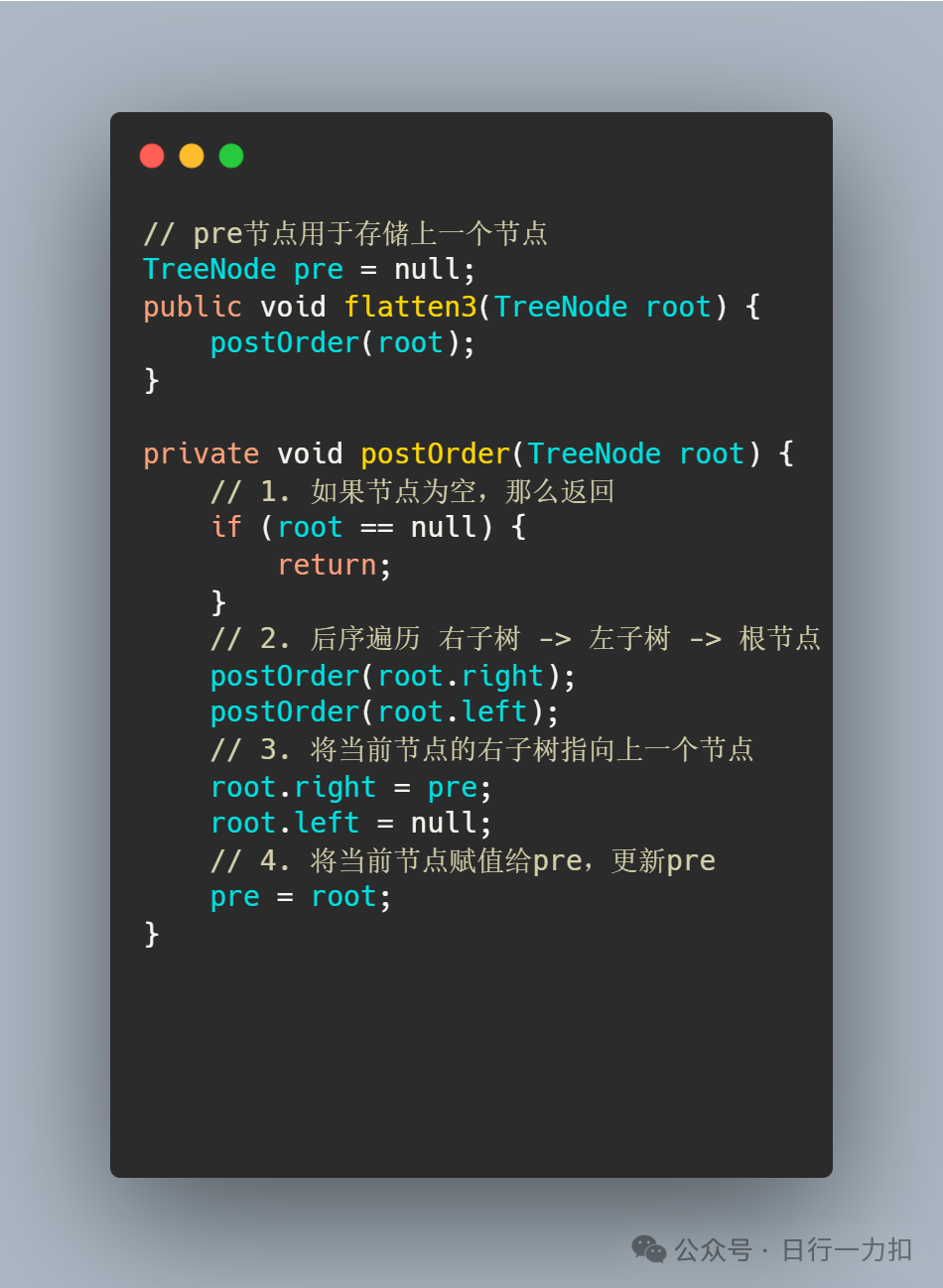
4. 相关复杂度分析
-
解法一:使用递归和栈
-
时间复杂度:O(n),其中 n 是二叉树中的节点数。递归函数
createLinkedList遍历了每个节点一次。 -
空间复杂度:O(h),其中 h 是二叉树的高度。在最坏情况下,栈的深度为 h,即二叉树的高度。
-
-
解法二:迭代方法
-
时间复杂度:O(n),其中 n 是二叉树中的节点数。每个节点最多被访问两次。
-
空间复杂度:O(1)。没有使用额外的空间,只使用了常数级别的额外空间。
-
-
解法三:使用递归和全局变量
-
时间复杂度:O(n),其中 n 是二叉树中的节点数。递归函数
postOrder遍历了每个节点一次。 -
空间复杂度:O(h),其中 h 是二叉树的高度。递归调用栈的深度取决于二叉树的高度。
-