一篇带你搞定数据结构散列表

ops/2024/12/21 21:20:35/

数据结构入门学习（全是干货）——散列表

1 散列表

1.1 引子：散列的基本思路

  • C语言变量名的管理：

    1. 定义/声明：先定义后使用。
    2. 插入与查找：
      • 插入：新变量定义。
      • 查找：检查变量是否已定义。

  • 动态查找问题：

    • 使用查找树（搜索树）进行变量管理，效率较低。
    • 字符串比较复杂，是否可以转换为数字以提高效率？即散列查找。

  • 已知查找方法：

    1. 顺序查找：效率低。
    2. 二分查找：需先排序。
    3. 二叉搜索树：效率较高。

  • 查找本质：

    • 目标：找对象位置。
    • 方法：散列，即直接计算位置，避免复杂比较。

1.2 什么是散列表

类型名称：符号表(SymbolTable)
数据对象集：符号表是“名字(Name)-属性(Attribute)”对的集合。
操作集：Table∈SymbolTable,Name∈NameType,Attr∈AttributeType
1.SymbolTable InitializeTable(int TableSize )://表的初始化创建一个长度为TableSize的符号表；
2.Boolean IsIn(SymbolTable Table,NameType Name)://判别一个对象是不是在这个表里查找特定的名字Name是否在符号表Table中；
3.AttributeType Find(SymbolTable Table,NameType Name)://在表里查找属性获取Table中指定名字Name对应的属性；
4.SymbolTable Modefy(SymbolTable Table,NameType Name,AttributeType Attr)：//把表中属性改掉将Table中指定名字Name的属性修改为Attr;
5.SymbolTable Insert(SymbolTable Table,NameType Name,AttributeType Attr)://在表里插入一个新的对象向Table中插入一个新名字Name及其属性Attr;
6、SymbolTable Delete(SymbolTable Table,NameType Name)://从表里删除从Table中删除一个名字Name及其属性。主要操作：上面的3、5、6

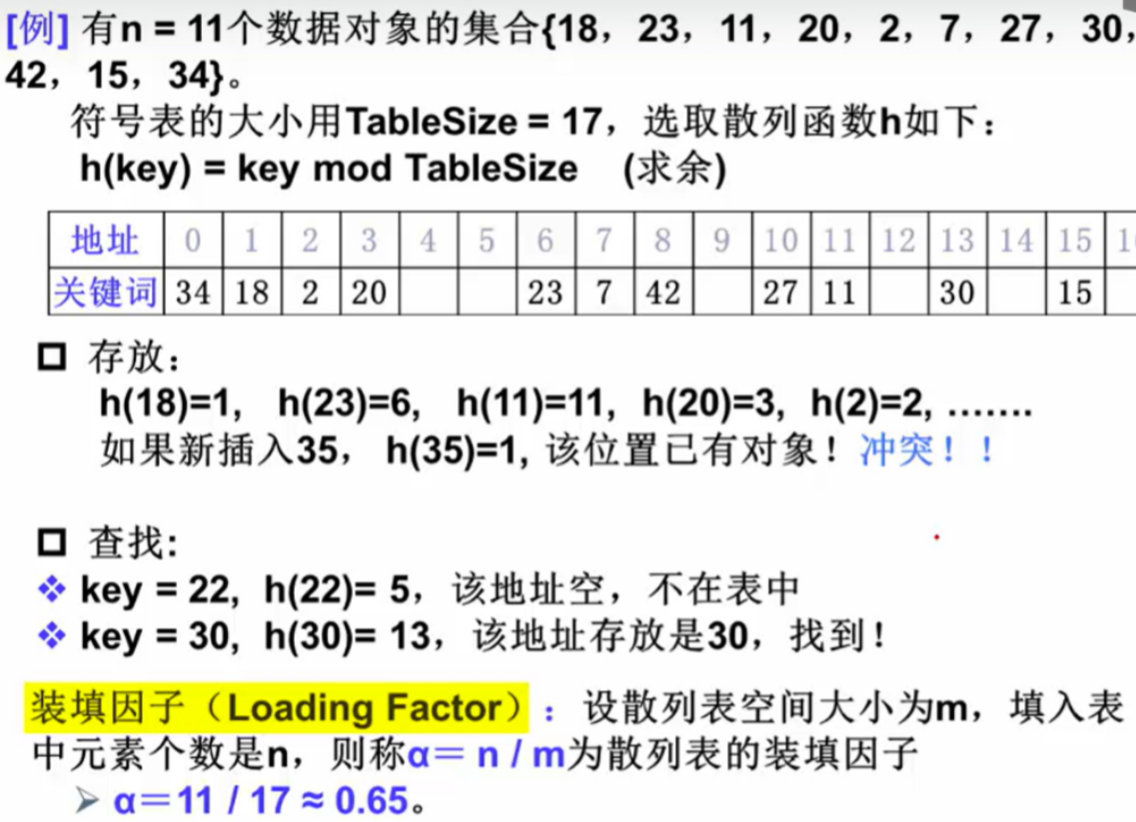
  • 装填因子：散列表被充满的程度。

  • 冲突设计：二维数组存储同一地址的元素，避免冲突。

    同一个地址的就放在同一行，有冲突的在所在那行后一列继续放，如图所示：

  • 哈希函数设计：确保高效存储与快速查找。

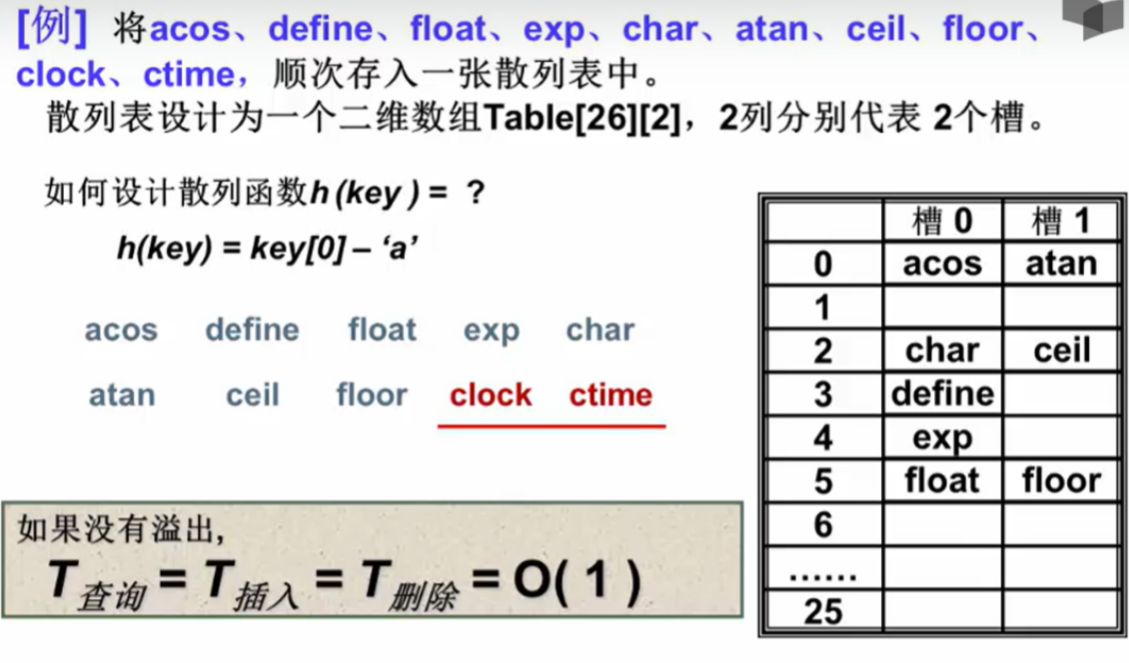
2 散列函数的构造方法

2.1 数字关键词的散列函数

一个"好"的散列函数一般应考虑下列两个因素：

  1. 计算简单，以便提高转换速度

  2. 关键词对应的地址空间分布均匀，以尽量减少冲突

  3. 直接定址法：h(key) = a × key + b。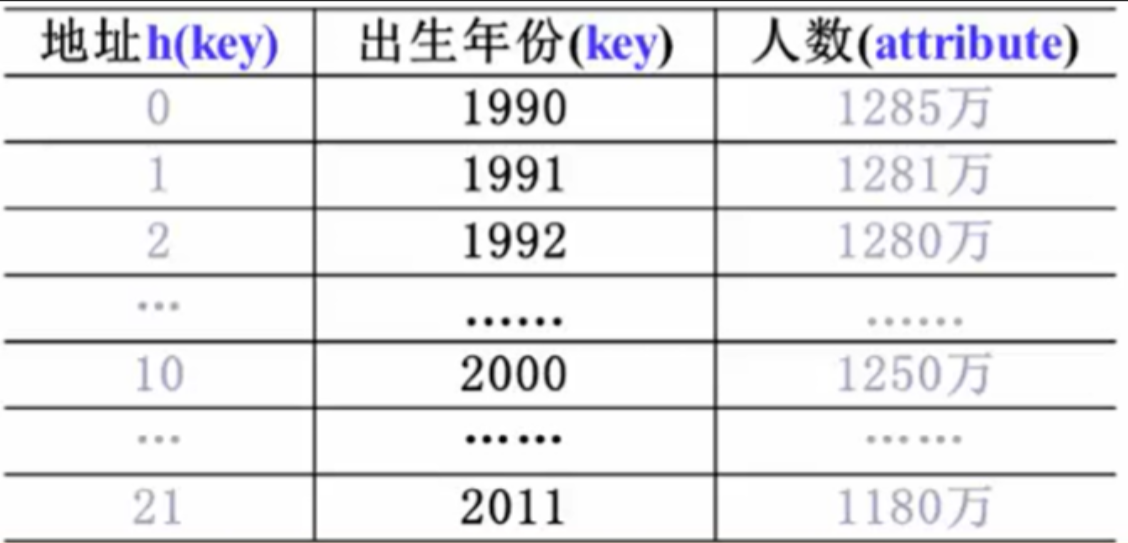

  4. 除留余数法：h(key) = key mod p。

  5. 数字分析法：根据数字关键字各位变化。

    1. 比如：取11位收集号码key的后4位作为地址：散列函数为：h(key)=atoi(key+7)

    1. 如果关键词key是18位的身份证号码：

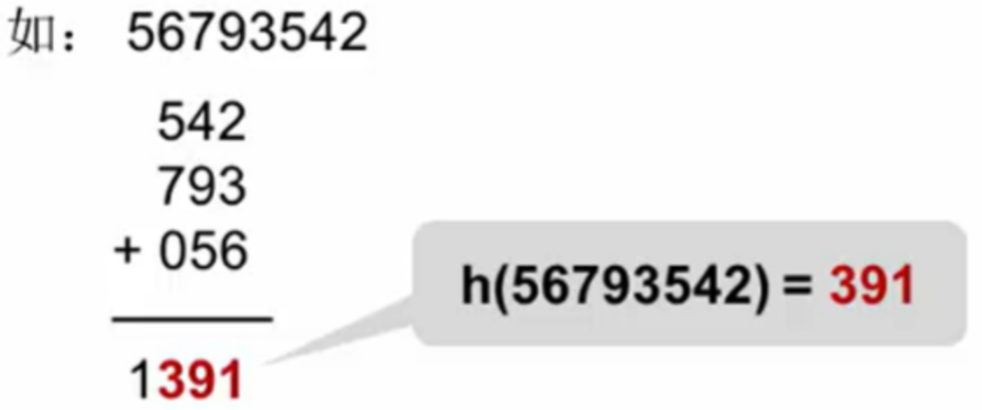
  6. 折叠法：将关键词分割并叠加。

  7. 平方取中法：取平方中间位。

    如果仅改变56793542的最后一位，观察散列值会有什么变化（原散列值为641）。

    请计算一下，按照平方取中法,key为56793543的散列值是多少=652

2.2 字符串关键词的散列函数

  1. ASCII码加和法：简单但易聚集。

  2. 前三个字符移位法：仍有冲突和空间浪费。

    • h(key)=(key[0] x 27² + key[1] x 27 + key[2])mod TableSize
    • 这种方法仍然会产生冲突：string、street、strong、structure等等(前三位是一样的)；空间浪费：3000/26³≈30
    • 空间浪费原因：字符一共有26种变化，所以三个字符的变化一共就26的三次方。而前三位一般出现的情况是3000种，而我们实际上考虑到26³去了，通过上面可以知道浪费的空间足足有30倍

  3. 移位法：改进散列函数，减少冲突。

    将数值巨大化，采用32进制相乘

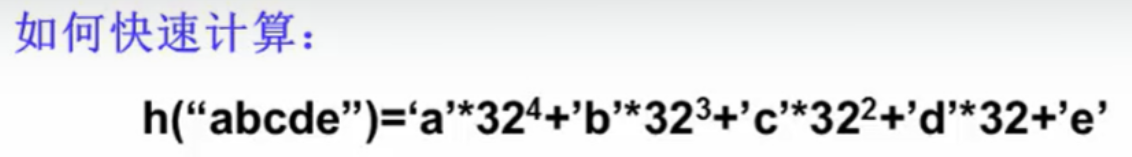
    优化方法：(a32+b) =>((a32+b)32+c)=>(((a32+b)32+c)32+d)

    如果直接计算'a'*32^4+'b'*32^3+'c'*32^2+'d'*32+'e'所需要的乘法总次数是4+3+2+1=10次。采用 ((('a'*32+'b')*32+'c')*32+'d')*32+'e'的计算方法，乘法总次数是多少？（顺便思考一下两者时间效率的差别）4

    
Index Hash(const char*Key,int TableSize)
{unsigned int h = 0;//散列函数值，初始化为0while(*Key != ‘\0’)//位移映射，这里就是值不为空的意思 h = ( h << 5 ) + *Key++;//h << 5是左移五位的意思return h % TableSize;//最后求余得到地址
}

3 冲突处理方法

3.1 开放定址法

  • 当冲突发生时，寻找空地址。

​

  • 常用方法：
    • 线性探测：简单但可能聚集。
    • 平方探测：冲突少，探测效率高。
    • 双散列：使用两个散列函数。

3.2 线性探测

  • 查找性能分析：成功与不成功的查找长度不同，冲突率影响效率。

会形成聚集现象

如果按照与刚才例子输入相反的顺序插入各个元素，这些元素在散列表中的位置还是一样的？不一样

散列表查找性能分析

  1. 成功平均查找长度(ASLs) => 就是我要找的对象最后被我找到了
  2. 不成功平均查找长度(ASLu) =>找对象找不着

什么是成功的 => 在散列表里找到的是成功的，不在散列表的元素就是不成功的

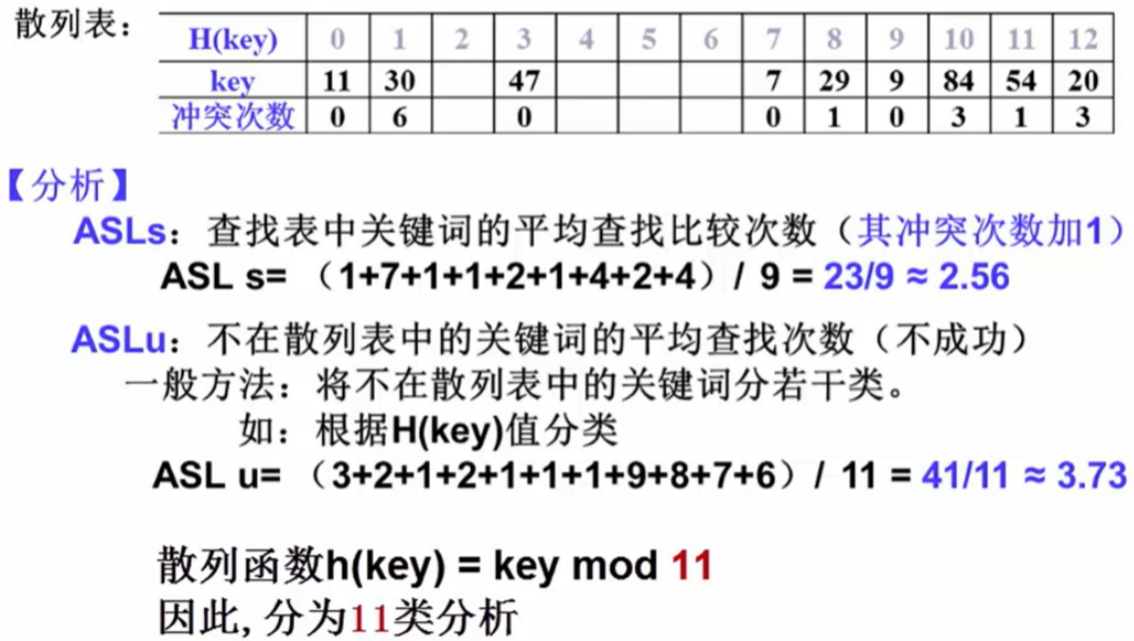
ASL u = 值(值取决于哈希余数)

余数为0要比较3次，为1要比较2次，余数为2要比较1次，余数为3的时候要比较2次，余数为4、5、6都是比较一次就够了，余数为7则要比较9次才能知道，余数为8则是8次

余数-哈希函数

  1. 余数的思想 所谓余数，就是程序中取模运算中的“模”。 余数具有一个非常重要的特性：可以将无限的数据归一到有限的范围（余数总是小于除数）
你知道，整数是没有边界的，它可能是正无穷，也可能是负无穷。但是余数却可以通过某一种关系，让整数处于一个确定的边界内。我想这也是人类发明星期或者礼拜的初衷吧，任你时光变迁，我都是以 7 天为一个周期，“周”而复始地过着确定的生活。因为从星期的角度看，不管你是哪一天，都会落到星期一到星期日的某一天里。
  1. 同余定理 在上边的例子中，第一天与第八天都是周一，第二天与第九天都是周二，即
1%7=8%7=12%7=9%7=2

这就引出了余数的另一个重要概念：同余定理

口语化表述：两个整数 a 和 b，如果它们除以正整数 m 得到的余数相等，我们就可以说 a 和 b 对于模 m 同余

其实，奇数与偶数的确定就是同余定理的应用。将一个数字模2，得0为偶数，得1为奇数 复杂算法拆解后的原理并不一定复杂，同余定理也可以作为有用的应用，就是哈希函数

哈希函数（散列函数）

将任意长度的输入，通过哈希算法，压缩为某一固定长度的输出，所得存储位置为散列地址

散列过程

（1）存储记录时，通过散列函数记录散列地址，按地址存储记录（2）查找记录时，通过同样的散列函数计算记录的散列地址，按散列地址访问记录

散列技术通过散列函数建立了从记录的关键码集合到散列表的地址集合的一个映射，显然，会出现两个不同记录存放在同一位置的情况，这种现象称为冲突，此时相同位置的记录称为同义词

散列函数中最常采用的方案是除留余数法，其基本思想：

选择适当的正整数P，以关键码除以P的余数作为散列地址通常P为小于或等于表长（最好接近）的最小质数或不包含小于 20 质因子的合数

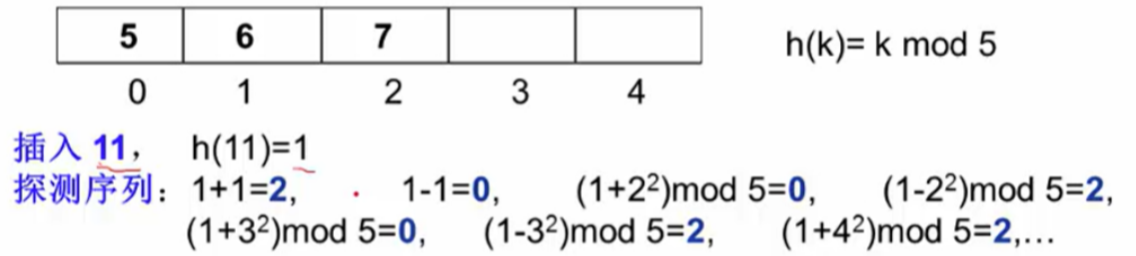
3.3 平方探测法

  • 二次探测，减少聚集现象。

是否有空间，平方探测(二次探测)就能找得到？

实现

typedef struct HashTbl*HashTable;
struct HashTbl{int TableSize;//当前表的实际大小Cell*TheCells;//代表自己是一个数组，实际上是一个指针
}H;HanshTable InitializeTable(int TableSize)
{HashTable H;int i;if( TableSize < MinTableSize ){//判别散列表的大小，太小就没必要做散列，直接放在数组就行了Error("散列表太小");return NULL;}//分配散列表H = (HashTable)malloc(sizeof(struct HashTbl));//申请空间赋给Hif( H == NULL )FatalError("空间溢出!!!");//判断有没有申请成功H->TableSize = NextPrime(TableSize);//申请成功的话希望表的size是素数，NextPrime就是这个目的，产生一个比表大一点的素数//分配散列表CellsH->TheCells=(Cell*)malloc(sizeof(Cell)*H->TableSize);//为真正的TableSize分配一个空间，就相当于指向一个数组了if(H->TheCells == NULL)FatalError("空间溢出!!!");for(i=0;i<H->TableSize;i++)H->TheCells[i].Info = Empty;return H;
}

友情小提示：typedef struct 的typedef是用来取别名的，比如上方 HashTbl 的别名就是H

实际删除的元素不能真的从表中拿掉，不然查找的时候会有问题的。如果我们要删除可以先做个记号。这样在后续的查找与插入的好处有：首先在查找的时候碰到被删掉的元素就说这个位置他做了个记号被删掉了，我们就知道这还不是空位还可以继续找，如果真拿掉变成空位的话就会产生误判。然后插入的时候发现这个元素是被删掉了，他不是空位而是原来有元素占着，现在被删掉了，这个时候插入元素就可以来替代原来删掉的元素。这样我们插入删除的操作都可以做并且不影响我们的查找过程

//表的初始化
Position Find(ElementType Key,HashTable H)//平方探测
{Position CurrentPos,NewPos;int CNum;//记录冲突次数CNum = 0;NewPos = CurrentPos = Hash(Key,H->TableSize);//要算哈希函数，所以先调用一个哈希函数。CurrentPos是我们值真正要放的位置 while(H->TheCells[NewPos].Info != Empty && H->TheCells[NewPos].Element != Key){//Info位置不空且Element值不等于我要找的Key，那就需要继续找，而循环的条件就是我们要找的位置，被别人占了但是不空//字符串类型的关键词需要strcmp函数if(++CNum % 2){//判断冲突的奇偶次NewPos = CurrentPos +(CNum+1)/2*(CNum+1)/2;//探测方法：在原来的位置上(CurrentPos，也就是最早的哈希函数值)加减i²获得新的地址。因为一会加一会减，所以需要在上方用上if来判别是奇数是偶来决定该加还是该减while(NewPos >= H->TableSize)//上方NewPos加上后面的大小可能超出大于TableSize了，所以需要通过不断循环减去TableSize，一直到NewPos不大于他(不大于他就落在0-TableSize之间了)NewPos -= H->TableSize;}else{//如果是偶数就走这条路啦，减去一个i平方NewPos = CurrentPos - CNum/2*CNum/2;while(NewPos < 0)//跟上面那个while类似，为了不负到突破地板，需要将值拉回来NewPos += H->TableSize;}}return NewPos;
}

映射为i的平方。CNum加1除以2就是这个i的值。所以举个例子

例子：1加1除以2为1，3加1除以2为2，5加1除以2为3

如果是减少的话，4除2为2，6除2为3

void Insert(ElementType Key,HashTable H)
{//插入操作Position Pos;Pos = Find(Key,H);//通过Find return出来一个position值if(H->TheCells[Pos].Info != Legitimate){//需要判断Pos的状态，如果Pos不属于被占用的状态，那我们这个元素就可以放进去(什么情况不是属于被别人占用：空位或者被删除了)//确认在此插入H->TheCells[Pos].Info = Legitimate;//将Info设为被我占用的状态，然后下一步将Key放进去H->TheCells[Pos].Element = Key;//字符串类型的关键词需要strcpy函数}
}
ps：在开放地址散列表中，删除操作要很小心。通常只能"懒惰删除"，即需要增加一个“删除标记(Deleted)”，而并不是真正删除它。以便查找时不会"断链"。其空间可以在下次插入时重用

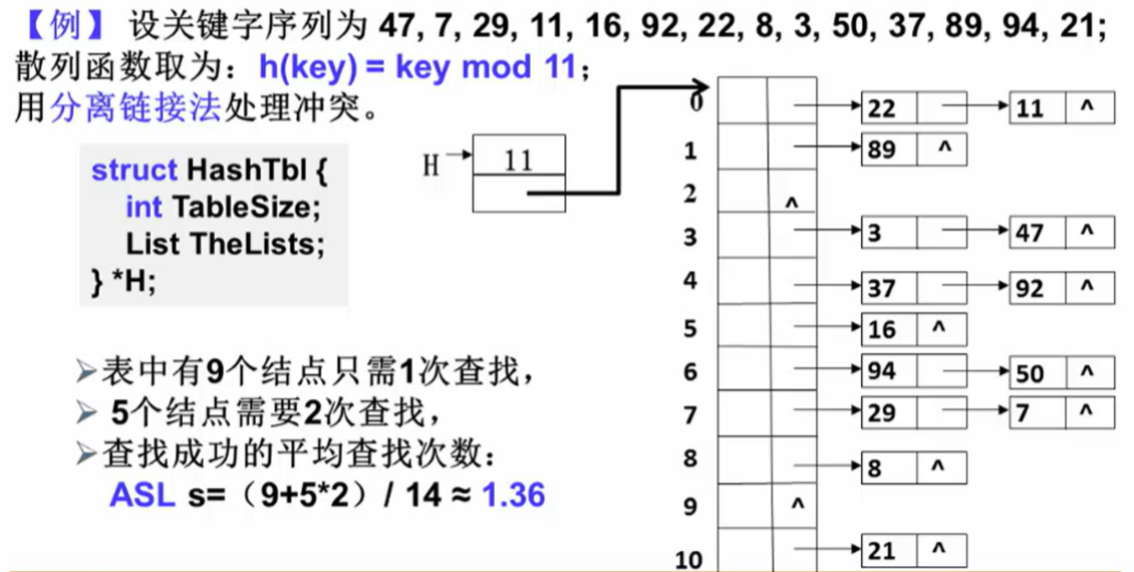
3.4 分离链接法

  • 冲突元素存储在链表中，避免聚集。

链表实现


typedef struct ListNode*Position,*List;
struct ListNode{ElementType Element;Position Next;//把Next分量分给P，P是下方代码块的一个指针，指向单项链表的第一个元素
};
typedef struct HashTbl*HashTable;
struct HashTbl{int TableSize;List TheLists;
};

Position Find(ElementType Key,HashTable H)//哈希表来表示
{Position P;int Pos;Pos = Hash(Key,H->TableSize);//初始散列位置，第一步算哈希函数值，得到散列函数散列地址，散列地址就代表他在这个数组里的位置P = H->TheLists[Pos].Next;//获得链表头，这个P就是上方代码块说的那个指针P，指向单项链表的第一个元素while(P != NULL && strcmp(P->Element,Key))//典型的遍历单项链表的循环，只要P不等于NULL，P所指向的这个元素跟我要找的这个元素不相等就一个个往后找，P的Next赋给P。意思就是只要P不空(后面还有元素)，那么循环就一直做，同时循环的另一个条件是当前的这个元素值不等于我要找的元素值，如果列表不空再找下一个，再下一个就P的Next赋给P//等循环退出来要么P空了，就return NULL(没找到)。要么就strcmp返回值等于0，等于0就相等了，那这个时候所在的这个节点就是我们找到了，也就是return PP = P->Next;return P;
}

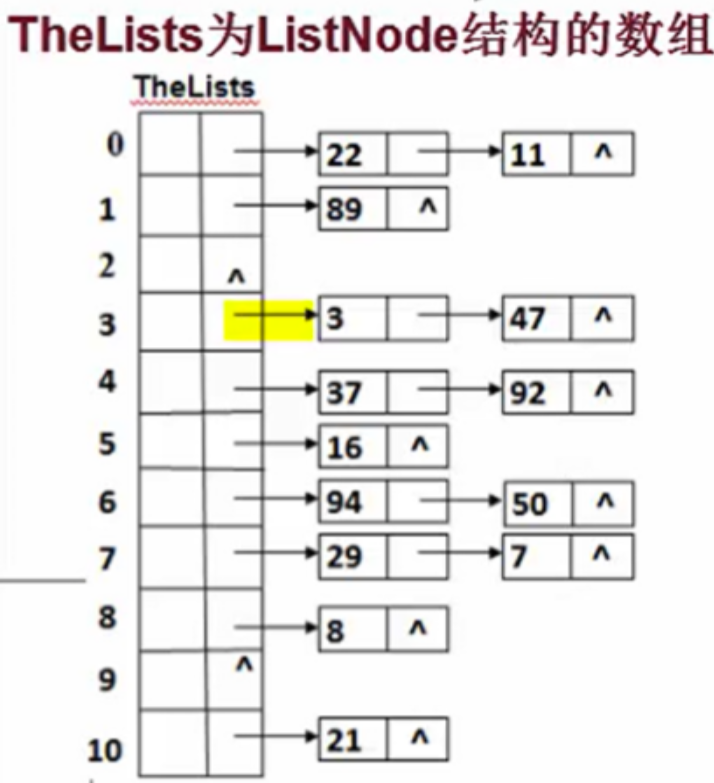
创建开放地址法的散列表

#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
typedef int ElementType;    /* 关键词类型用整型 */
typedef int Index;          /* 散列地址类型 */
typedef Index Position;     /* 数据所在位置与散列地址是同一类型 */
/* 散列单元状态类型，分别对应：有合法元素、空单元、有已删除元素 */
typedef enum { Legitimate, Empty, Deleted } EntryType;typedef struct HashEntry Cell; /* 散列表单元类型 */
struct HashEntry{ElementType Data; /* 存放元素 */EntryType Info;   /* 单元状态 */
};typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */int TableSize; /* 表的最大长度 */Cell *Cells;   /* 存放散列单元数据的数组 */
};int NextPrime( int N )
{ /* 返回大于N且不超过MAXTABLESIZE的最小素数 */int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */while( p <= MAXTABLESIZE ) {for( i=(int)sqrt(p); i>2; i-- )if ( !(p%i) ) break; /* p不是素数 */if ( i==2 ) break; /* for正常结束，说明p是素数 */else  p += 2; /* 否则试探下一个奇数 */}return p;
}HashTable CreateTable( int TableSize )
{HashTable H;int i;H = (HashTable)malloc(sizeof(struct TblNode));/* 保证散列表最大长度是素数 */H->TableSize = NextPrime(TableSize);/* 声明单元数组 */H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));/* 初始化单元状态为“空单元” */for( i=0; i<H->TableSize; i++ )H->Cells[i].Info = Empty;return H;
}

平方探测法的查找与插入

Position Find( HashTable H, ElementType Key )
{Position CurrentPos, NewPos;int CNum = 0; /* 记录冲突次数 */NewPos = CurrentPos = Hash( Key, H->TableSize ); /* 初始散列位置 *//* 当该位置的单元非空，并且不是要找的元素时，发生冲突 */while( H->Cells[NewPos].Info!=Empty && H->Cells[NewPos].Data!=Key ) {/* 字符串类型的关键词需要 strcmp 函数!! *//* 统计1次冲突，并判断奇偶次 */if( ++CNum%2 ){ /* 奇数次冲突 */NewPos = CurrentPos + (CNum+1)*(CNum+1)/4; /* 增量为+[(CNum+1)/2]^2 */if ( NewPos >= H->TableSize )NewPos = NewPos % H->TableSize; /* 调整为合法地址 */}else { /* 偶数次冲突 */NewPos = CurrentPos - CNum*CNum/4; /* 增量为-(CNum/2)^2 */while( NewPos < 0 )NewPos += H->TableSize; /* 调整为合法地址 */}}return NewPos; /* 此时NewPos或者是Key的位置，或者是一个空单元的位置（表示找不到）*/
}bool Insert( HashTable H, ElementType Key )
{Position Pos = Find( H, Key ); /* 先检查Key是否已经存在 */if( H->Cells[Pos].Info != Legitimate ) { /* 如果这个单元没有被占，说明Key可以插入在此 */H->Cells[Pos].Info = Legitimate;H->Cells[Pos].Data = Key;/*字符串类型的关键词需要 strcpy 函数!! */return true;}else {printf("键值已存在");return false;}
}

分离链接法的散列表实现

#define KEYLENGTH 15                   /* 关键词字符串的最大长度 */
{HashTable H;int i;H = (HashTable)malloc(sizeof(struct TblNode));/* 保证散列表最大长度是素数，具体见代码5.3 */H->TableSize = NextPrime(TableSize);/* 以下分配链表头结点数组 */H->Heads = (List)malloc(H->TableSize*sizeof(struct LNode));/* 初始化表头结点 */for( i=0; i<H->TableSize; i++ ) {H->Heads[i].Data[0] = '\0';H->Heads[i].Next = NULL;}return H;
}Position Find( HashTable H, ElementType Key )
{Position P;Index Pos;Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */P = H->Heads[Pos].Next; /* 从该链表的第1个结点开始 *//* 当未到表尾，并且Key未找到时 */ while( P && strcmp(P->Data, Key) )P = P->Next;return P; /* 此时P或者指向找到的结点，或者为NULL */
}bool Insert( HashTable H, ElementType Key )
{Position P, NewCell;Index Pos;P = Find( H, Key );if ( !P ) { /* 关键词未找到，可以插入 */NewCell = (Position)malloc(sizeof(struct LNode));strcpy(NewCell->Data, Key);Pos = Hash( Key, H->TableSize ); /* 初始散列位置 *//* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */NewCell->Next = H->Heads[Pos].Next;H->Heads[Pos].Next = NewCell; return true;}else { /* 关键词已存在 */printf("键值已存在");return false;}
}void DestroyTable( HashTable H )
{int i;Position P, Tmp;/* 释放每个链表的结点 */for( i=0; i<H->TableSize; i++ ) {P = H->Heads[i].Next;while( P ) {Tmp = P->Next;free( P );P = Tmp;}}free( H->Heads ); /* 释放头结点数组 */free( H );        /* 释放散列表结点 */
}

4 散列表的性能分析

  1. 平均查找长度(ASL)用来度量散列表查找效率：成功、不成功

    1. 成功：查找的元素再散列表里
    2. 不成功：查找的元素不在散列表里

  2. 关键词的比较次数，取决于产生冲突的多少。影响产生充裕多少有以下三个因素：

    1. 散列函数是否均匀(不均匀的话冲突会多，性能就会差)
    2. 处理冲突的方法
    3. 散列表的装填因子α(装了多少元素，装的元素少那么冲突少。装的元素多则冲突多)
  • 平均查找长度(ASL)：
    • 成功与不成功查找性能。
    • 影响因素：散列函数均匀性、冲突处理方法、装填因子。

分析：不同冲突处理方法、装填因子对效率的影响

  1. 线性探测法的查找性能 可以证明，线性探测法的期望探测次数满足下列公式：

  2. 对于线性探测，如果当前装填因子值为0.654321, 此时不成功情况下的期望探测次数小于成功情况下的期望探测次数。错误

  3. 平方 探测法和双散列探测法的查找性能 可以证明，平方探测法和双散列探测法探测次数 满足下列公式：

期望探测次数与装填因子α的关系

横坐标：装填因子α

纵坐标：期望探测次数

当装填因子α＜0.5的时候，各种探测法的期望探测次数都不大，也比较接近

合理的最大装入因子α应该不超过0.85(对线性探测来说)

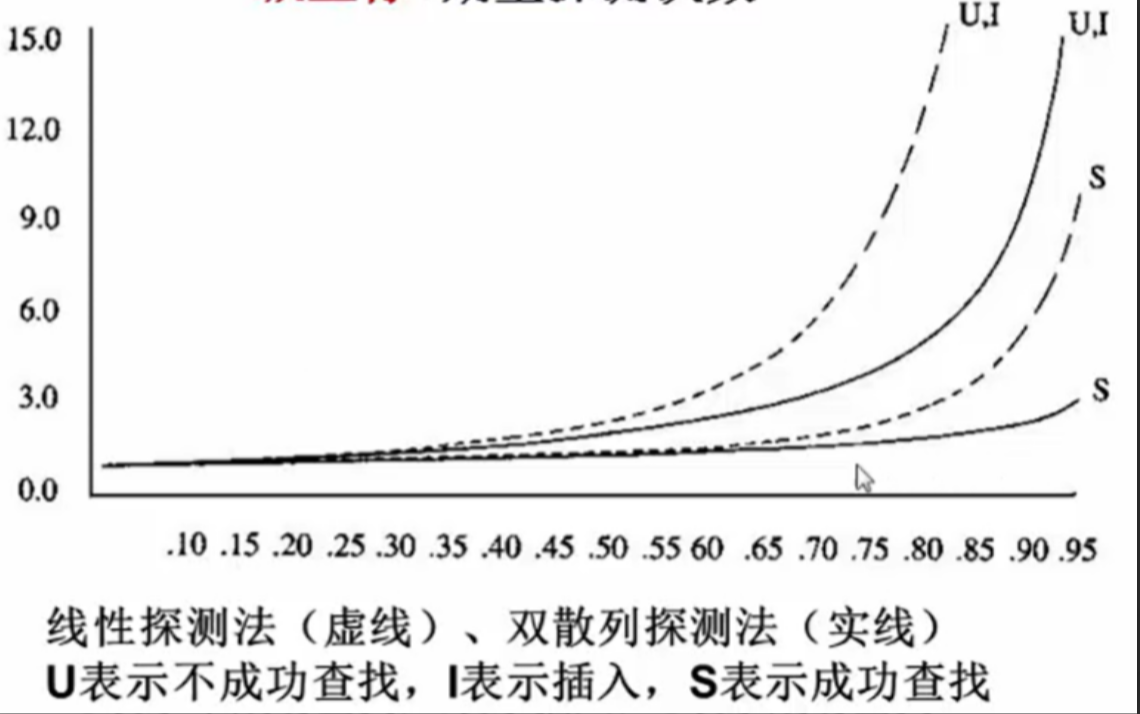
  1. 分离链接法的查找性能

    所有地址链表的平均长度定义成装填因子α，α有可能超过1 不难证明：其期望探测次数p为

5 应用实例：词频统计

  • 问题描述：统计电话次数，寻找“电话聊天狂人”。
  • 解法：
    1. 排序法：简单但不适合动态插入。
    2. 直接映射法：存储效率高，但空间占用大。
    3. 散列法：高效处理动态数据。

代码示例

#define MAXTABLESIZE 1000000int NextPrime(int N) {int i, p = (N % 2) ? N + 2 : N + 1; // 从大于N的下一个奇数开始while (p <= MAXTABLESIZE) {for (i = (int)sqrt(p); i > 2; i--)if (!(p % i)) break; // p不是素数if (i == 2) break; // p是素数else p += 2; // 尝试下一个奇数}return p;
}HashTable CreateTable(int TableSize) {HashTable H;int i;H = (HashTable)malloc(sizeof(struct TblNode));H->TableSize = NextPrime(TableSize);H->Heads = (List)malloc(H->TableSize * sizeof(struct LNode));for (i = 0; i < H->TableSize; i++) {H->Heads[i].Data[0] = '\0'; H->Heads[i].Next = NULL;H->Heads[i].Count = 0; // 初始化头节点}return H;
}int Hash(int Key, int P) {return Key % P; // 散列函数
}Position Find(HashTable H, ElementType Key) {Position P;Index Pos;Pos = Hash(atoi(Key + KEYLENGTH - MAXD), H->TableSize); // 取后五位P = H->Heads[Pos].Next; // 从链表开始查找while (P && strcmp(P->Data, Key)) {P = P->Next;}return P; // 找到的节点或NULL
}bool Insert(HashTable H, ElementType Key) {Position P, NewCell;Index Pos;P = Find(H, Key);if (!P) { // 关键词未找到，可以插入NewCell = (Position)malloc(sizeof(struct LNode));strcpy(NewCell->Data, Key);NewCell->Count = 1; // 初始化计数器Pos = Hash(atoi(Key + KEYLENGTH - MAXD), H->TableSize);NewCell->Next = H->Heads[Pos].Next;H->Heads[Pos].Next = NewCell;return true;} else {P->Count++; // 增加计数return false;}
}

http://www.ppmy.cn/ops/117273.html

相关文章

SpringSecurity -- 入门使用

SpringSecurity -- 入门使用

文章目录 什么是 SpringSesurity &#xff1f;细节使用方法 什么是 SpringSesurity &#xff1f; 在我们的开发中&#xff0c;安全还是有些必要的 用 拦截器 和 过滤器 写代码还是比较麻烦。 SpringSecurity 是 SpringBoot 的底层安全默认选型。一般我们需要认证和授权&#xf…
阅读更多...
HTML与JavaScript结合实现简易计算器

HTML与JavaScript结合实现简易计算器

目录 背景&#xff1a; 过程&#xff1a; 代码: HTML部分解析&#xff1a; body部分解析&#xff1a; JavaScript部分解析&#xff1a; 效果图 &#xff1a; 总结: 背景&#xff1a; 计算器是一个典型的HTML和javaScript结合使用的例子&#xff0c;它展示了如何使用H…
阅读更多...
【完整梳理验证】企业微信第三方应用接入全流程java版

【完整梳理验证】企业微信第三方应用接入全流程java版

企业微信第三方应用接入全流程java版 1. 概念与流程1.1 概念1、企业内部应用2、`第三方应用`3、代开发自建应用1.2 流程1.2.1 全局流程1.2.2 应用配置1.2.3 数据流程2. 核心文档2.1 理解第三方应用开发流程和概念2.1.1 应用开发阶段2.1.2 应用推广阶段2.1.3 基本流程1）前期应用…
阅读更多...
海信智能电视的使用心得

海信智能电视的使用心得

买了海信智能电视(型号:32E2F)有一段时间了&#xff0c;要使用这个智能电视还真能考验你的智商。海信电视有很多优点&#xff0c;它的屏幕比较靓丽&#xff0c;色彩好看&#xff0c;遥控器不用对着屏幕就能操作。但也有不少缺点。 1. 海信智能电视会强迫自动更新操作系统&…
阅读更多...
C++ bitset（位图）的模拟实现

C++ bitset（位图）的模拟实现

文章目录 一、bitset接口总览二、bitset模拟实现1. 构造函数2. set、reset、flip、test3. size、count4. any、none、all5. 打印函数 三、完整代码 一、bitset接口总览 成员函数功能set设置指定位或所有位为1&#xff08;即设置为“已设置”状态&#xff09;reset清空指定位或…
阅读更多...
Entity Framework扩展高级查询功能

Entity Framework扩展高级查询功能

需求&#xff1a;前端按照格式传递查询条件参数&#xff0c;后端自动解析。 前端参数格式&#xff1a;[{"f":"","v":"","o":"","t":"",}]。 参数f&#xff1a;参数名。 参数v&#xff1a;参…
阅读更多...
如何使用代理提高您在SNKRS抽奖中的成功率

如何使用代理提高您在SNKRS抽奖中的成功率

在抢购限量运动鞋时&#xff0c;SNKRS抽奖是一种常见的方式。但由于竞争激烈&#xff0c;成功率往往较低。使用代理服务可以帮助您提高中奖的机会&#xff0c;以下是一些具体的策略。 一、避免IP封锁 在SNKRS抽奖中&#xff0c;过于频繁的请求可能导致您的IP被封锁。通过使用…
阅读更多...
VCS的常用仿真命令（持续更新）

VCS的常用仿真命令（持续更新）

书接上回&#xff1a; VCS的常用编译命令 仿真命令 1. 执行run过程 命令&#xff1a;Simv 结果&#xff1a;此时会生成一个ucli.key文件。该文件的作用是&#xff1a;如果事先在该文件里写好了ucli命令&#xff0c;仿真过程中会读取这些ucli命令执行相关的操作&#xff0c;而…
阅读更多...
最新文章

Copyright @ 2022~2023