当我们从扫描设备获取点云数据时,数据会包含噪声和伪影,点云噪声特性包括不真实的点、孤立点、不规则,基于噪声特性对器进行去除;
统计滤波 Statistical Outlier Removal(SOR)(去除离群点)
-
滤波思想
对每一个点的邻域进行一个统计分析,计算它到所有临近点的平均距离。假设得到的结果是一个高斯分布,其形状是由均值和标准差决定,那么平均距离在标准范围(由全局距离平均值和方差定义)之外的点,可以被定义为离群点并从数据中去除。 -
接口函数
remove_statistical_outlier(self, nb_neighbors, std_ratio, print_progress=False)

当判断点与nb_neighbors个近邻点的平均距离大于【平均距离+std_ratio*σ】,即判定为噪声点,一般取std_ratio=2或3为极限误差;
- 测试
import open3d as o3d
# 加载点云
pcd = o3d.io.read_point_cloud("./data/desk.pcd")
# 统计滤波
k = 20 # K邻域点的个数
μ = 2.0 # 标准差乘数
sor_pcd, idx = pcd.remove_statistical_outlier(k, μ)#当判断点的k近邻的平均距离大于【平均距离+μ*σ】,即判定为噪声点,一般取μ=2或3为极限误差
sor_pcd.paint_uniform_color([0, 0, 1])
# 提取噪声点云
sor_noise_pcd = pcd.select_by_index(idx, invert=True)
sor_noise_pcd.paint_uniform_color([1, 0, 0])
o3d.visualization.draw_geometries([sor_pcd,sor_noise_pcd], window_name="SOR")

半径滤波 Radius Outier Removal
-
滤波思想
在给定阈值参数MinPts后,遍历点云所有点,对于点云中任意一点,设其半径R内有K个点,当K< MinPts时,即可识别该点为噪声点,并该点去除。 -
接口函数
remove_radius_outlier(self, nb_points, radius, print_progress=False)

其中,nb_points:邻域球内的最少点个数,小于该个数为噪声点;
radius:邻域半径大小;
当判断点的nb_points近邻平均距离大于【平均距离+μ*σ】,即判定为噪声点;
- 测试
import open3d as o3d# 加载点云
pcd = o3d.io.read_point_cloud("./data/desk.pcd")
# 半径滤波
MinPts = 5 # 邻域球内的最少点个数,小于该个数为噪声点
R = 0.05 # 邻域半径大小# pc 去噪后的点云
# idx 去噪保留的点索引
pc, idx = pcd.remove_radius_outlier(MinPts, R)pc.paint_uniform_color([0, 0, 1])
ror_noise_pcd = pcd.select_by_index(idx,invert = True)
ror_noise_pcd.paint_uniform_color([1, 0, 0])
o3d.visualization.draw_geometries([pc, ror_noise_pcd], window_name="半径滤波")

引导滤波 Guilter Filter
- 滤波思想
引导滤波假设点云经过一个线性变换,具有很好的保留边缘信息功能;Guided Filter一般用来对2D图像进行降噪等处理,实际上,稍作修改后可以对3D点云进行降噪。针对点云的Guided Filter算法,可概况为
-
计算点云中某一个点pi的领域 N ( i ) N ( i ) N(i);
-
求 N ( i ) N ( i ) N(i)中所有点的均值 u i u_i ui 和协方差 Σ i Σ_i Σi;
-
根据公式计算 A k A_k Ak和 b k b_k bk;
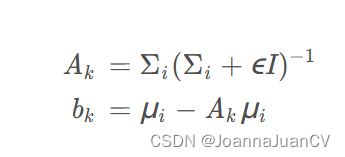
-
q i = A k p i + b k q_i =A_k p_i +b_k qi=Akpi+bk, 输出 q i q_i qi 作为对点 p i p_i pi 的滤波结果;
- python 源码
- 测试
import numpy as np
import open3d as o3d#guild filter
def guided_filter(pcd, radius, epsilon):kdtree = o3d.geometry.KDTreeFlann(pcd)points_copy = np.array(pcd.points)points = np.asarray(pcd.points)num_points = len(pcd.points)for i in range(num_points):k, idx, _ = kdtree.search_radius_vector_3d(pcd.points[i], radius)if k < 3:continueneighbors = points[idx, :]mean = np.mean(neighbors, 0)cov = np.cov(neighbors.T)e = np.linalg.inv(cov + epsilon * np.eye(3))A = cov @ eb = mean - A @ meanpoints_copy[i] = A @ points[i] + bpcd.points = o3d.utility.Vector3dVector(points_copy)#添加噪声
def add_noise(pcd, sigma):points = np.asarray(pcd.points)noise = sigma * np.random.randn(points.shape[0], points.shape[1])points += noisepcd = o3d.io.read_point_cloud('./data/bunny.ply')
add_noise(pcd, 0.004)
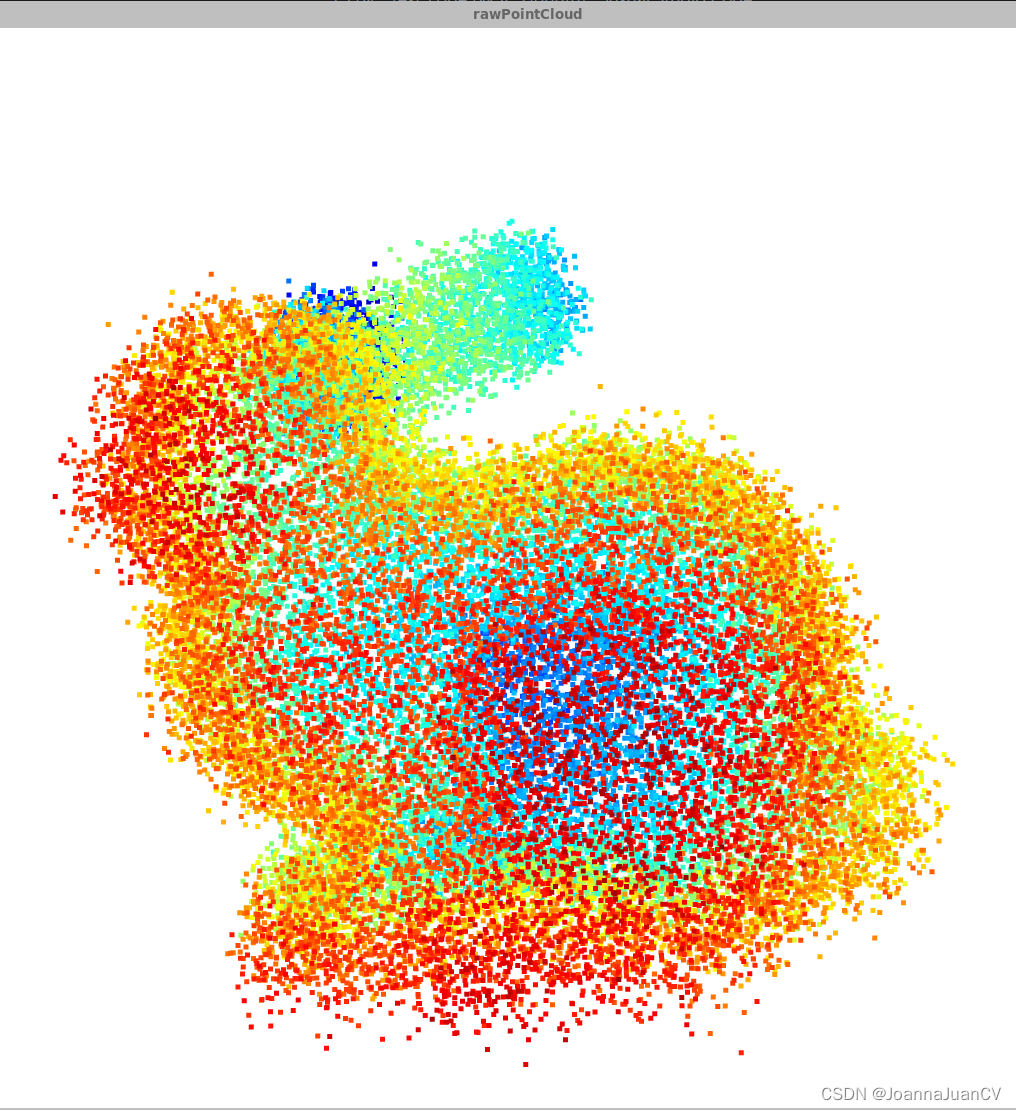
o3d.visualization.draw_geometries([pcd],window_name="rawPointCloud")
guided_filter(pcd, 0.01, 0.1)
guided_filter(pcd, 0.01, 0.1)
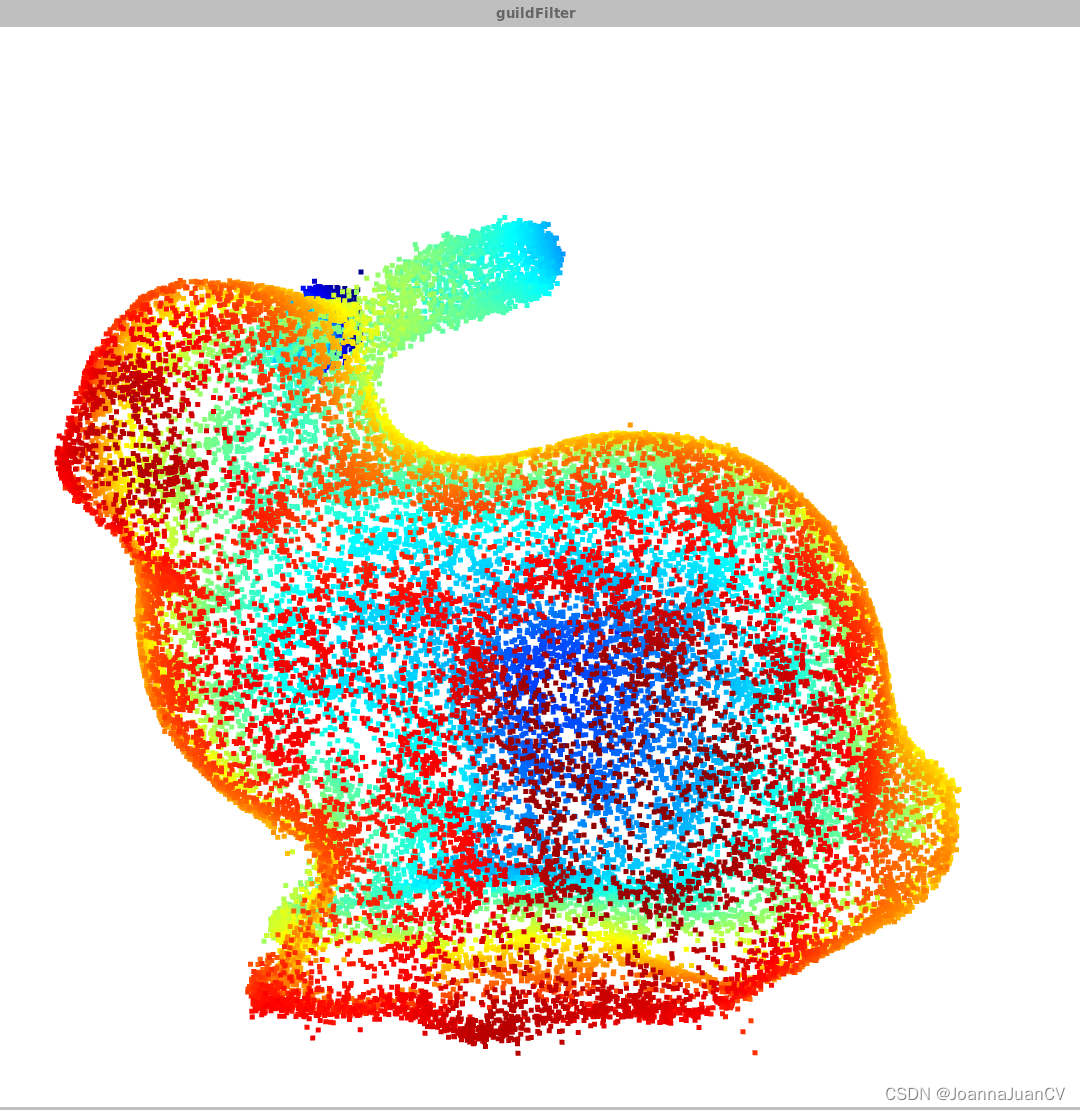
o3d.visualization.draw_geometries([pcd],window_name="guildFilter")