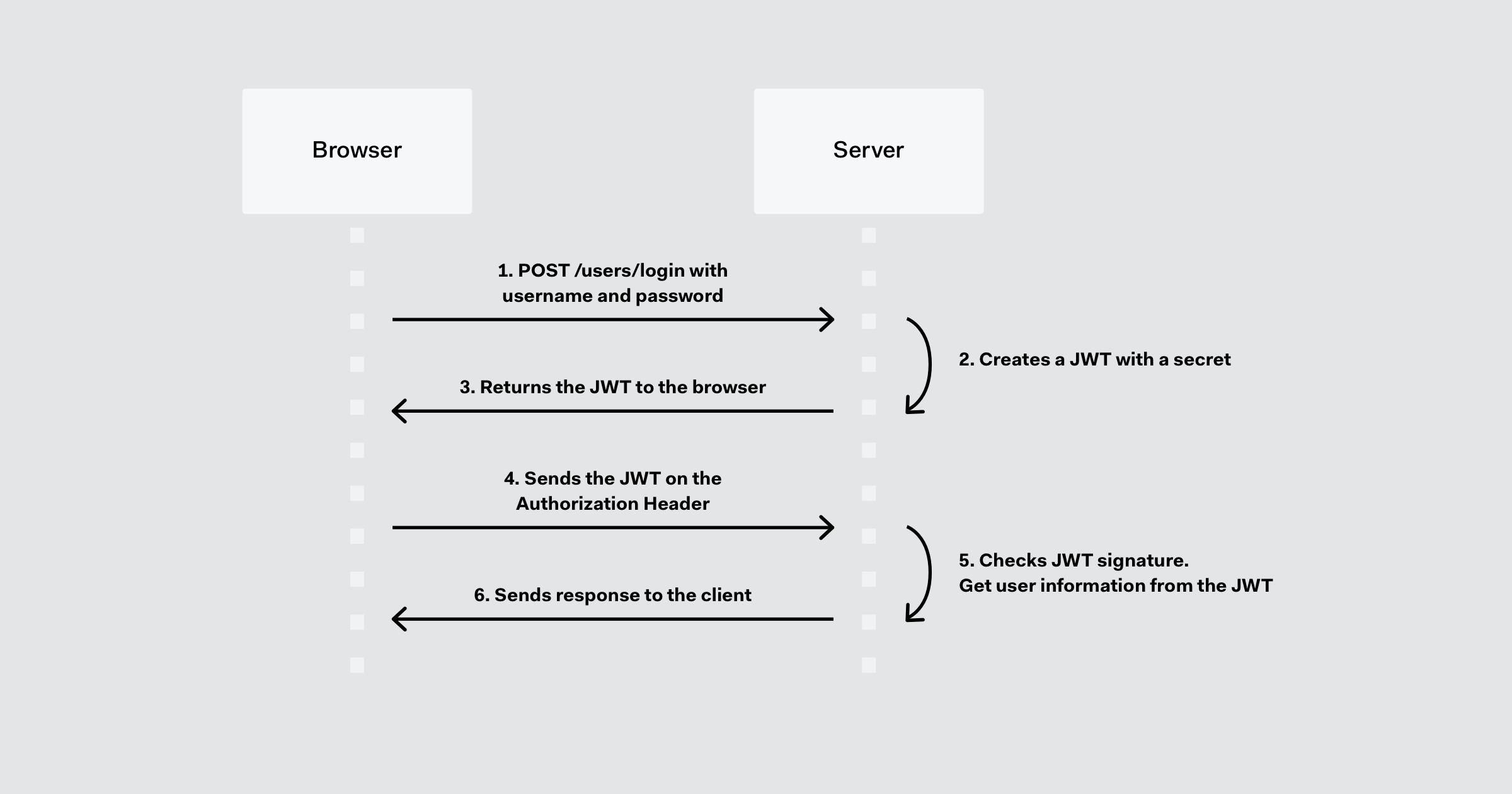
先行控制技术

缓冲深度的设计方法

以先行指令缓冲栈为例。

假设缓冲深度为$D_1$，考虑以下两种极端情况。

（1）先行指令缓冲栈已经充满，此时指令流出速度最快，例如连续分析RR型指令 ，设这种指令序列的最大长度为$L_1$，平均分析一条指令的时间为$t_1$；同时，指令流入的速度最慢，平均取一条指令的时间为$t_2$，从主存取到先行指令缓冲栈中的指令数为$L_1-D_I$。应该满足以下关系：

$L_1{t}_1=(L_1-D_I)t_2$

$D_I=\lceil \frac{L_1\times (t_2-t_1)}{t_2}\rceil$

可以预见时间$L_1{t}_1$之后，缓冲栈变空，失去作用。因此必须保证这种指令流的连续长度不超过$L_1$。通过对程序进行静态分析以确定$L_1$的值来计算出缓冲深度$D_I$。

（2）先行指令缓冲栈原来为空，此时指令流出速度最慢，指令流入的速度最快。

控制相关

通过转移预测技术降低控制相关带来的损失。

（1）通过编译器尽量降低转移成功的概率。

（2）设置两个先行指令缓冲栈，按照转移成功的方向预取指令到先行目标缓冲栈，先行指令缓冲栈仍然按照转移不成功的方向继续预取指令。如果转移不成功，则继续分析原来先行指令缓冲栈中的指令；如果转移成功，则分析新增设的先行目标缓冲栈中的指令。Don’t put all your eggs in one basket.

流水线技术

线性流水线的性能分析

1. 吞吐率

   设$n$为任务数，$T_k$为完成$n$个任务所用的时间，则流水线的吞吐率为$TP=\frac{n}{T_k}$。

   假设各段执行时间相等，输入连续任务的情况下，完成$n$个任务需要的总时间为$T_k=(k+n-1)\times \Delta t$，其中$k$为流水线的段数，$\Delta t$为时钟周期。最大的吞吐率为$T{P}_{max}=li{m}_{n\to \infty }\frac{n}{(k+n-1)\Delta t}=\frac{1}{\Delta t}$

   若各段时间不等，完成连续$n$个任务（可以想象到其他流水段会出现一些“气泡”等待最长的流水段执行）：

   $TP=\frac{n}{{\sum }_{i=1}^k\Delta t_i+(n-1)max(\Delta t_1,...,\Delta t_k)}$

   $T{P}_{max}=\frac{1}{max(\Delta t_1,...,\Delta t_k)}$

2. 加速比（Speedup）

   加速比的基本公式：$S=\frac{顺序执行时间T_0}{流水线执行时间T_k}$

3. 效率（Efficiency）

   计算流水线效率的一般公式：$E=\frac{n个任务占用的时空区}{k个流水段的总的时空区}=\frac{T_0}{k\times T_k}$

4. 流水线最佳段数的选择

   采用顺序执行方式完成一个任务的时间为$t$，在同等速度的$k$段流水线上执行一个任务的时间为$\frac{t}{k}+d$，$d$为流水锁存器的延迟时间，因此，流水线的最大吞吐率为$P=\frac{1}{\frac{t}{k}+d}$，流水线的总价格估计为$C=a+bk$，其中$a$为功能段身的总价格，$b$为每个锁存器的价格。

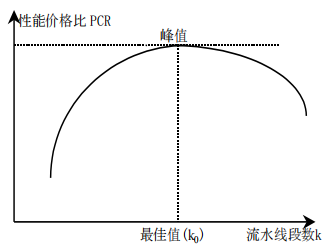
   我们可以定义一个“性价比”，性能和价格比PCR定义为

   $PCR=\frac{P}{C}=\frac{1}{\frac{t}{k}+d}\times \frac{1}{a+bk}$

   令导数为0得到$(\frac{k}{t+kd}\times \frac{1}{a+bk}{)}^{\prime }=0$

   解得$k_0=\sqrt{\frac{t\times a}{d\times b}}$

非线性流水线的冲突问题

在非线性流水线中，会出现几个任务用同一流水段的情况。

无冲突调度方法

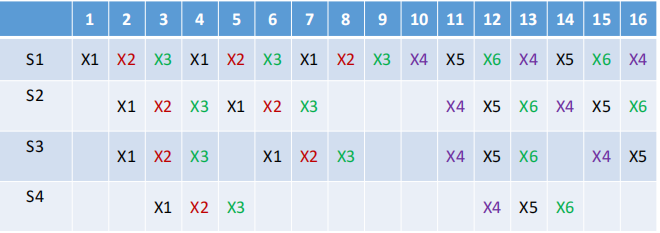
首先定义一些概念：

启动距离：连续输入两个任务之间的距离。

禁止向量：预约表中每一行任意两个X之间距离的集合。下例中为(3,4,6)，可以预见用禁止向量中的数作为下一个任务的启动距离会导致流水线的冲突。

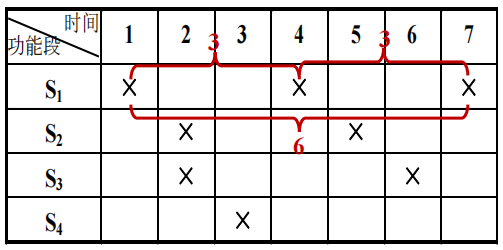
冲突向量：$C=(C_m{C}_{m-1}...C_2{C}_1)$，其中$m$是禁止向量中的最大值，如果$i$在禁止向量中则$C_i=1$，否则$C_i=0$。因此，(3,4,6)对应冲突向量(101100)。

1. 将冲突向量逻辑右移（模拟时间流动），若移出去的是1，则表示用相应启动距离向流水线输入新任务时会导致功能段冲突。

2. 若移出去的是0，则表示不会产生功能段冲突。添加该任务，用移位之后的向量（前一个任务在流水线中的剩余部分）和初始的冲突向量按位或得到新的冲突向量。

3. 对新的冲突向量做同样的操作。实际上每个冲突向量是一个状态。根据步骤2中的变换关系（移多少位添加新任务）可以构建出状态图，实际上就是有限状态自动机（DFA）。

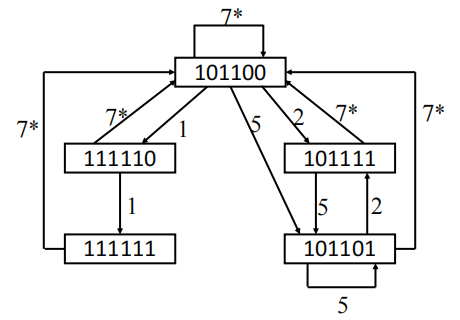
对于上面的例子，一个任务执行7个时间片，因此启动距离为7时流水线已经排空，上一个任务已经结束。因此，所有状态均有一条7*的弧连向初始冲突向量。

定义简单循环为在状态图中各种冲突向量只经过一次的启动循环。下图为最小启动循环的(1,1,7)的预约表。