什么是队列？

在上一篇文章中讲述了栈：先进后出就是栈，队列刚好相反，先进先出的数据结构就是队列，还是拿纸箱子来举例：队列可以理解为一个没有底的纸箱子，往箱子里面放书，一本一本叠上去，但是全都从下面漏掉了，最先放进去的书就最先调出来。或者从字面意思来理解，队列就像是生活中排队买票一样，排在前面的人先买到票，后面的人后买到票。

队列主要包含两个操作：入队（在队列尾部插入一个数据）和出队（从队列头部删除一个数据），和栈类似，队列也是一种操作受限的线性表数据结构，队列可以用数组来实现，也可以用链表来实现。

在使用数组实现的队列中，入队的时间复杂度是O(1)，出队的时间复杂度是O(n)，查找元素的时间复杂度是O(n)。
在使用链表实现的队列中，入队和出队的时间复杂度都是O(1)，查找元素的时间复杂度是O(n)。

队列中需要定义两个指针：一个是指向队头的head 指针，另一个是指向队尾的 tail 指针。在二叉树的层序遍历和图的广度优先搜索算法中可以使用队列来实现，后面再说。

下面是使用Go语言的数组实现队列操作的代码：

// go-algo-demo/queue/QueueArray.go
type ArrayQueue struct {data     []interface{} //存放队列数据capacity int           //队列容量head     int           //对头位置tail     int           //队尾位置
}// 初始化队列
func NewArrayQueue(n int) *ArrayQueue {return &ArrayQueue{make([]interface{}, n), n, 0, 0}
}// 入队
func (this *ArrayQueue) Enqueue(v interface{}) bool {if this.tail == this.capacity { //如果队尾的位置和容量相等,说明队列已满return false}this.data[this.tail] = vthis.tail++return true
}// 出队
func (this *ArrayQueue) Dequeue() interface{} {if this.head == this.tail { //如果队头的位置和队尾的位置相等,说明队列已空return nil}v := this.data[this.head]this.head++return v
}// 格式化输出
func (this *ArrayQueue) String() string {if this.head == this.tail {return "empty queue"}result := ""for i := this.head; i <= this.tail-1; i++ {result += fmt.Sprintf("%v ", this.data[i])}return result
}func main() {queue := NewArrayQueue(5)//尝试给容量为5的队列入队6个元素,实际也只能入队成功5个元素queue.Enqueue(1)queue.Enqueue(2)queue.Enqueue(3)queue.Enqueue(4)queue.Enqueue(5)queue.Enqueue(6)fmt.Println(queue) //1 2 3 4 5//出队1个元素queue.Dequeue()fmt.Println(queue) // 2 3 4 5//出队3个元素queue.Dequeue()queue.Dequeue()queue.Dequeue()fmt.Println(queue) //5//再把最后一个元素出队queue.Dequeue()fmt.Println(queue) //empty queue
}

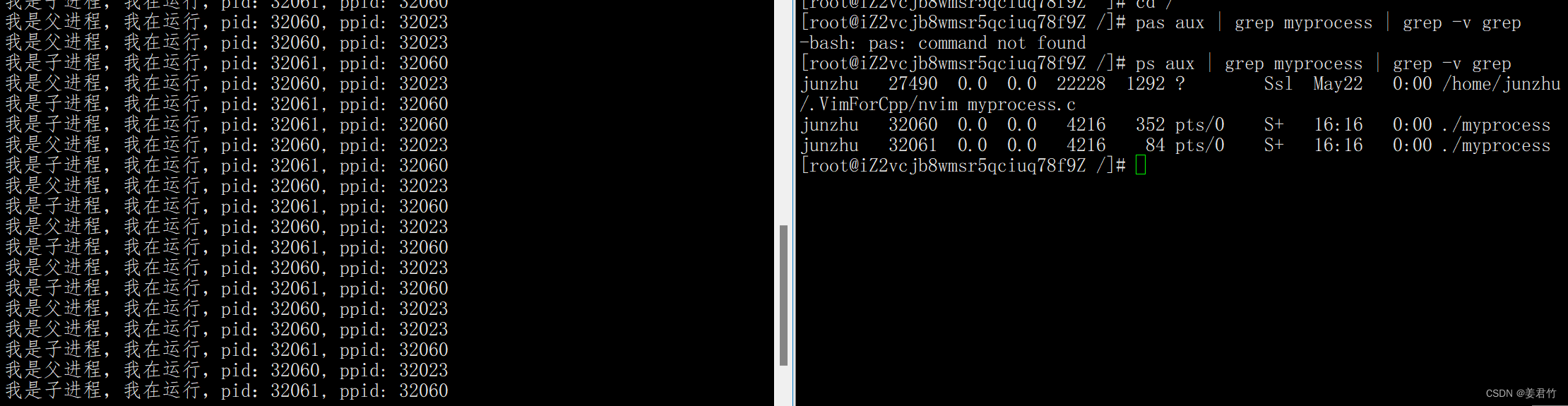
上面代码基于数组实现了一个队列，由于数组的删除操作会导致数组中的数据不连续，每次出队操作都要删除数组下标为 0 的数据，也就是要搬移下标为0后面的整个队列中的数据，因此队列出队操作的时间复杂度是 O(n)。对于这个问题，可以采用如下优化方案：在出队的时候不搬移数据，而是把head指针往后移动一位，在入队的时候判断如果队列中没有空闲空间了，再集中触发一次数据的搬移操作。比如下面图中所示，将元素A从队列中出队，剩余的元素都不动，只把对头指针往后移动一位。

循环队列

把普通队列的对头和队尾连接起来，就是一个循环队列，就像是一个圆环一样。使用循环队列可以解决数组越界问题。在循环队列中，最关键是要确定好队空和队满的判定条件。

循环队列新增元素时（即入队操作），需要判断队列是否已满，如果未满则可以将新元素赋值给队尾，然后让tail指针向后移动一个位置；如果已经排到了队列的最后位置，则将tail指针重新指向头部。
循环队列删除元素时（即出队操作），需要判断队列是否为空，如果不为空则将队头元素赋值给返回值，然后让head指针向后移动一个位置；如果已经排到了队列的最后位置，就把head指针重新指向头部。

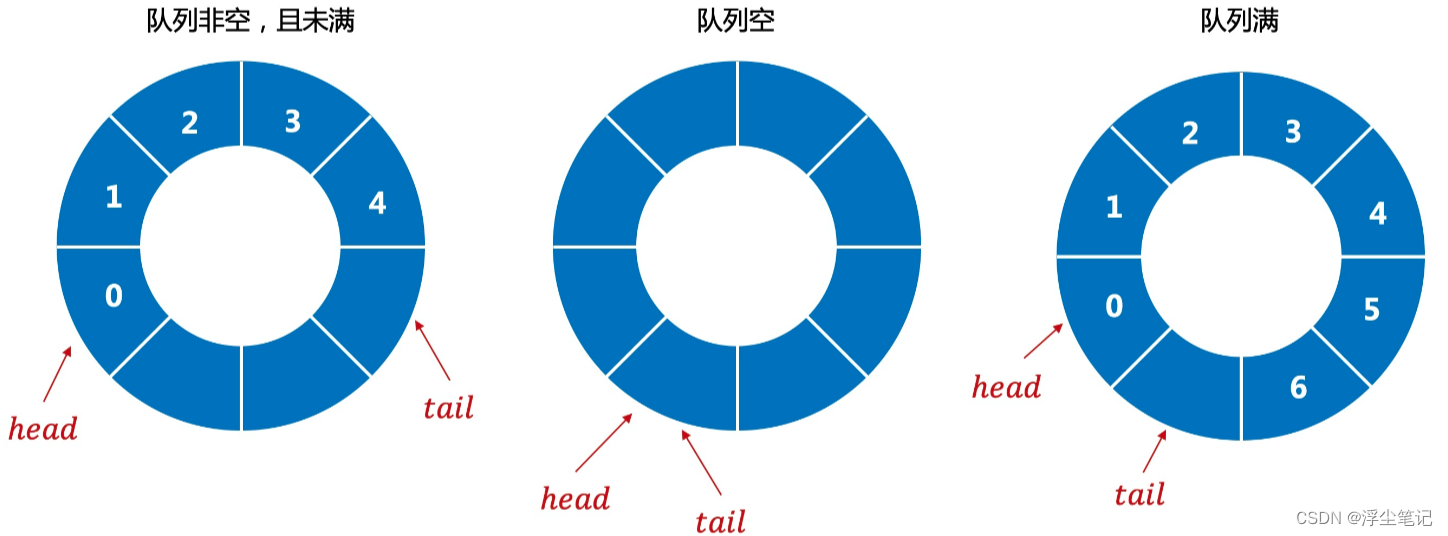
包含n个元素的循环队列中（假设容量为capacity），判断循环队列为空的条件是 head == tail，判断队列已满有个规律如下： (tail + 1) % capacity = head，循环队列已满时，上面第三张图中的 tail 指向的位置实际上是没有存储数据的，所以循环队列会浪费一个数组的存储空间。循环队列的入队操作和出队操作的时间复杂度都是O(1)。

上面第三张图的头尾指针带入 (tail + 1) % capacity = head 的公式后，计算可得：(7+1)%8=0；再换一个位置，假如 head=3，tail=2，那么 (2+1)%8=3

其实还有一个办法判断循环队列是否已满，而且不需要浪费一个存储空间，那就是定义一个可以容纳k个元素的循环队列，再多定义一个变量used（表示当前数组已存储的数据容量），判断used是否和k相等。但是考虑到在多线程编程中，控制变量越少越能最大可能实现无锁编程，因此推荐上面浪费一个存储空间而少定义一个变量的方式。另外，如果是使用链表实现的循环队列中不存在这个问题。

使用Go语言实现一个循环队列的核心代码如下：

// go-algo-demo/queue/CycleQueue.go// 队列为空的条件: (head == tail) 为 true
func (this *CycleQueue) IsEmpty() bool {if this.head == this.tail {return true}return false
}// 队列已满条件: ((tail+1)%capacity == head) 为 true
func (this *CycleQueue) IsFull() bool {if this.head == (this.tail+1) % this.capacity {return true}return false
}// 入队
func (this *CycleQueue) Enqueue(v interface{}) bool {if this.IsFull() {return false}this.queue[this.tail] = vthis.tail = (this.tail + 1) % this.capacityreturn true
}// 出队
func (this *CycleQueue) Dequeue() interface{} {if this.IsEmpty() {return nil}v := this.queue[this.head]this.head = (this.head + 1) % this.capacityreturn v
}

双端队列

双端队列，顾名思义就是头尾两端都可以FIFO 入队和出队的队列，入队和出队的时间复杂度都是O(1)。如下图所示：

阻塞队列

阻塞队列是在队列为空或者已满的时候，读取数据或者插入数据的特殊情况，具体情况如下：

当阻塞队列为空的时候，因为此时队列里面还没有数据，如果从队头取数据会被阻塞，直到队列中有了数据后才能返回；
当阻塞队列已经满了，那么像队列中插入数据就会阻塞，直到队列中有空闲位置后才能成功插入数据；

根据上面两个规则，可以发现阻塞队列就是一个 “生产者——消费者模型”，使用这种数据结构可以有效地协调生产和消费的速度，当消费者消费数据的速度太慢，队列就会很容易满，然后生产者就阻塞等待，直到消费者消费了数据，生产者才会继续生产。如果消费者消费的速度太慢，可以多配置几个消费者来加快消费的速度，这样的解决方案可以实现数据的削峰填谷。比较流行的消息队列 kafka、rabbitmq 底层就是使用了这样的原理。

举个例子，比如有个家具厂（生产者）每天能生产100个沙发，但是一辆车（消费者）每天只能运输20个沙发，要想不让生产出来的沙发出现堆积，就应该增加到每天五辆车来运输。

Redis中的 BRPOP和BLPOP 就是阻塞队列，可以点击 redis笔记03-链表和哈希_浮尘笔记的博客-CSDN博客查看具体用法。

队列的应用场景

对于大部分资源有限的场景，当没有空闲资源时，基本上都可以通过“队列”这种数据结构来实现请求排队。比如某个线程池中已经没有了空闲线程，当新的任务请求线程资源时，可以选择非阻塞的队列，直接拒绝任务请求；也可以选择阻塞队列对新来的请求排队，等到有空闲线程时再取出排队的请求继续处理。还有在操作系统上，CPU会根据同时请求的进程进行排队，根据“先进先出”的原则，最先进入队列的进程优先执行，然后再出队。

基于链表实现的无界队列（支持无限排队），但是也可能会导致过多的请求排队等待，请求处理的响应时间过长，这种方式不适合对响应时间要求比较高的系统；
基于数组实现的有界队列（队列的大小有限），当线程池中排队的请求超过队列大小时，后面新来的请求就会被拒绝，这种方式比较适合对响应时间要求比较高的系统，但是要注意设置一个合理的队列大小。

每日一练

力扣26. 删除有序数组中的重复项

给你一个升序排列的数组 nums ，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。

示例：输入：nums = [0,0,1,1,1,2,2,3,3,4]，输出：5

生活例子：作品获奖的人上台领奖品，如果一个人获得了多份奖，也只会领一份奖品。

方法1：因为已经说了是排好序的数组，所以只需要不停判断当前位置值和下一位置值是否相等。若相等则pop掉当前值，否则move到下一位置继续做判断。时间复杂度是 O(n^2)，因为每一次pop操作都需要将被删除元素后面的所有元素向前移动一格。

func removeDuplicates1(nums []int) (int, []int) {idx := 0for idx < len(nums)-1 {if nums[idx] == nums[idx+1] {nums = append(nums[:idx], nums[idx+1:]...) // 若相等则pop掉当前值} else { // 否则move到下一位置继续做判断idx += 1}}return len(nums), nums
}func main() {fmt.Println(removeDuplicates1([]int{0, 0, 1, 1, 1, 2, 2, 3, 3, 4})) //5 [0 1 2 3 4]
}

方法2：不停地往后遍历数组，同时自增地分配不重复的值给前面的位置，对于重复的直接跳过。时间复杂度就是O(n)。

func removeDuplicates2(nums []int) int {idx := 0for _, num := range nums {// 如果是第一位数,肯定不可能重复// 为了保证数组不越界,因此要判断 num != nums[idx-1]if (idx < 1) || (num != nums[idx-1]) {nums[idx] = num // 如果当前元素不是重复值，就将这个元素分配到目前不重复元素到达的indexidx += 1}}return idx
}func main() {fmt.Println(removeDuplicates2([]int{0, 0, 1, 1, 1, 2, 2, 3, 3, 4})) //5
}

源代码：https://gitee.com/rxbook/go-algo-demo/tree/master/queue