104. 二叉树的最大深度

学了回溯之后再来做一下

思路：

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

dfs，bfs，迭代三个方法都可以做这道题；

代码：

//  dfs
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftMax = maxDepth(root.left);int rightMax = maxDepth(root.right);return Math.max(leftMax, rightMax) + 1;}
}// bfs
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {int len = queue.size();for (int i = 0; i < len; i++) {TreeNode node = queue.poll();if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}depth++;}return depth;}
}class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}// 不影响if (root.left == null && root.right == null) {return 1;}int l = maxDepth(root.left);int r = maxDepth(root.right);return Math.max(l, r) + 1;}
}

559. N 叉树的最大深度

代码：

/*
// Definition for a Node.
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/class Solution {public int maxDepth(Node root) {if (root == null) {return 0;}int depth = 0;for (int i = 0; i < root.children.size(); i++) {depth = Math.max(depth, maxDepth(root.children.get(i)));}return depth + 1;}
}

111. 二叉树的最小深度

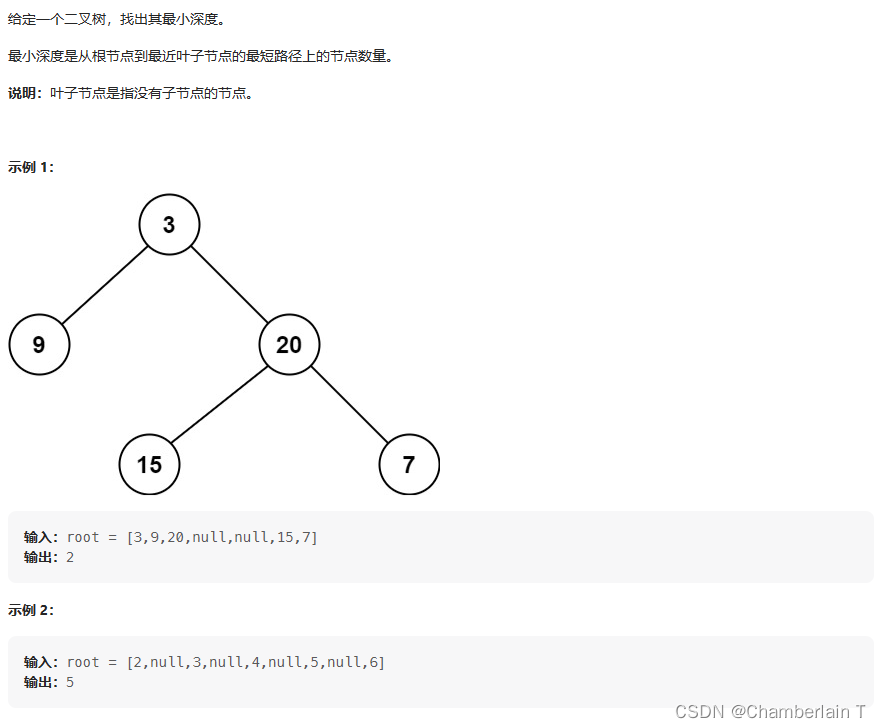
思路：

叶子节点是指左右节点都为空的情况，不能直接比较左右子树的最小深度，需要加以限制。例如[1, null, 2]，的最小深度为2，但如果直接取左右最小深度则容易算成1。

· 所以需要分情况：如果左子树为空，则最小深度为右子树最小深度+1；如果右子树为空，最小深度为左子树最小深度+1。左右子树都不为空，再去二者较小的深度+1；

代码：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*///  dfs
// 叶子节点是指左右孩子都为空的节点
class Solution {public int minDepth(TreeNode root) {if (root == null) {return 0;}int left = minDepth(root.left);int right = minDepth(root.right);// 左右孩子都为空if (root.left == null && root.right == null) {return 1;}// 只有左孩子为空if (root.left == null) {return right + 1;} // 只有右孩子为空if (root.right == null) {return left + 1;}// 左右孩子都不为空return Math.min(left, right) + 1;}
}// bfs
class Solution {public int minDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int minD = 0;while (!queue.isEmpty()) {int len = queue.size();minD++;for (int i = 0; i < len; i++) {TreeNode node = queue.poll();// 层序遍历，左右节点为空说明是叶子节点，第一个叶子节点对应最小深度if (node.left == null && node.right == null) {return minD;}if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}}return minD;}
}

222. 完全二叉树的节点个数

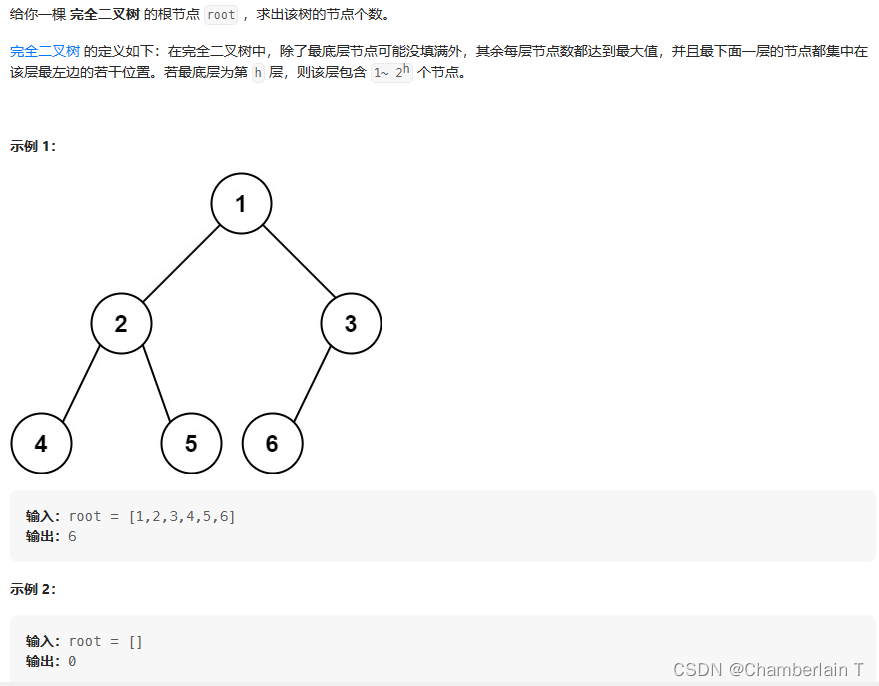
思路：

愉快的简单题。

代码：

// dfs
class Solution {public int countNodes(TreeNode root) {if (root == null) {return 0;}return countNodes(root.left) + countNodes(root.right) + 1;}
}class Solution {public int countNodes(TreeNode root) {return root == null? 0: countNodes(root.left) + countNodes(root.right) + 1;}
}// 迭代前序
class Solution {public int countNodes(TreeNode root) {int count = 0;if (root == null) {return count;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();count++;if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}      return count;}
}