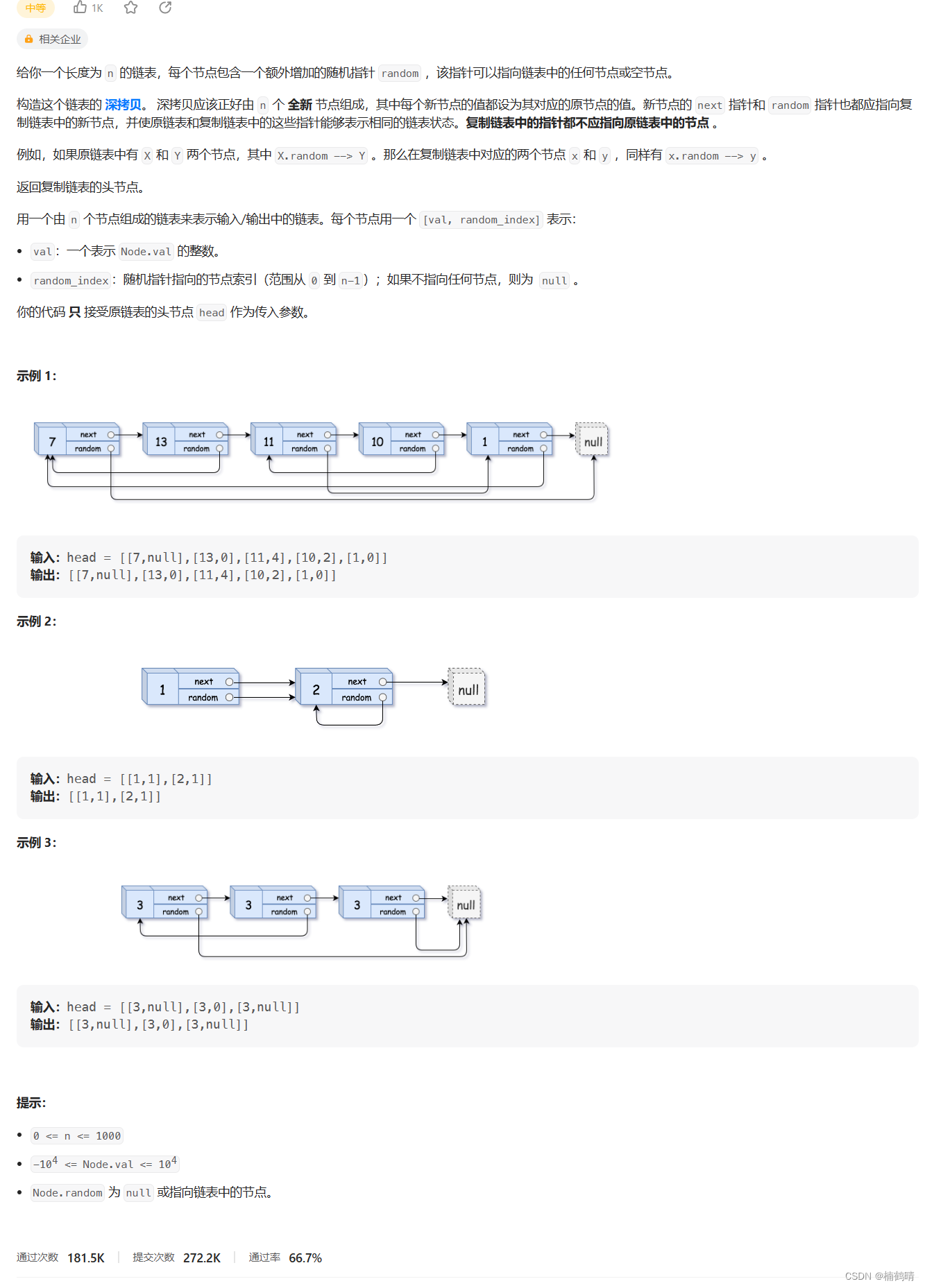
今天在学习的过程中偶然看到了一个博客,总结Ax=b的,那么我也写一篇。
首先就是判断A的秩和(A|b)的秩之间的关系,然后通过这个关系来进行进一步地判断。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
求解方法:

编辑切换为居中
添加图片注释,不超过 140 字(可选)
第一个是LU分解,相信大家都已经很熟悉了,这种计算的话形式非常好看,但是分析其加法和乘法的次数可以知道,这种做法并没有加快矩阵计算。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
Cholesky分解,这个证明过程就是利用了LU分解来进行证明的,同理,这个也没有加快矩阵的计算,只是在计算过程中,外表显得更加优雅。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
QR分解,其中Q是酉矩阵,但是Q还是大部分被认为是正交矩阵,在实数域上。QR分解用于稳定求解病态最小二乘问题,因此QR分解是最小二乘问题的好帮手。并且QR分解可以将相机矩阵转换为一个旋转矩阵和一个上三角的标定矩阵,这里的相机矩阵没看懂,可能是内参矩阵K?不知道,但是从后面这个转换成旋转矩阵和标定矩阵来看的话,感觉QR分解的功能还是非常强大的。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这个奇异值分解的作用也很大,在SLAM后端的优化过程中,可以配合最小二乘来进行问题的解决。

编辑切换为居中
添加图片注释,不超过 140 字(可选)

编辑切换为居中
添加图片注释,不超过 140 字(可选)
知道特征值和奇异值之间的关系,特征值是对应奇异值的平方。其中特征值代表了数据的离散程度,这个在机器学习的面试中可能会问到!特征值越大,则特征值代表的那个方向上的数据就越离散,那么其可区分度就越高。
然后这里还有一种Ax=b无解的情况,就是说这个方程是超定方程。那么此时我们可以用最小二乘拟合来对这个方程进行求解,ATAx=ATb这个方程就是求解最小二乘拟合系数的,通过这个方程进算出来的x称为最小二乘意义下的最优解,这个在SLAM问题中是经常用到的,而且如果你研究生阶段是研究SLAM的后端的话,那么这个最小二乘可能是你面试时候经常遇到的问题。