🥇2.3.2 合并排序

🥇2.3.3 快速排序

🌼P1010 [NOIP1998 普及组] 幂次方

🌳总结

形象点，分治正如“凡治众如治寡，分数是也”，管理少数几个人，即可统领全军

本质，将一个大规模问题分解为若干规模较小的相同子问题，分而治之

分治求解步骤：分解 --> 治理 --> 合并

大问题难以解决，就分解成规模更小的相同问题，各个子问题形式相同，解决方法也一样，所以可以使用递归算法快速解决。

🥇2.3.2 合并排序

就合并排序来说，如果只有一个数，那么它本身就是有序的；

如果有2个数，进行一次比较就可以完成排序

但是加入有1000，10000甚至10万个数呢

我们可以将其分解为小的数列，直到只剩一个数，本身已经有序，再将这些单个有序的数列合并在一起，执行一个和分解相反的过程，从而完成对整个序列的排序

图解

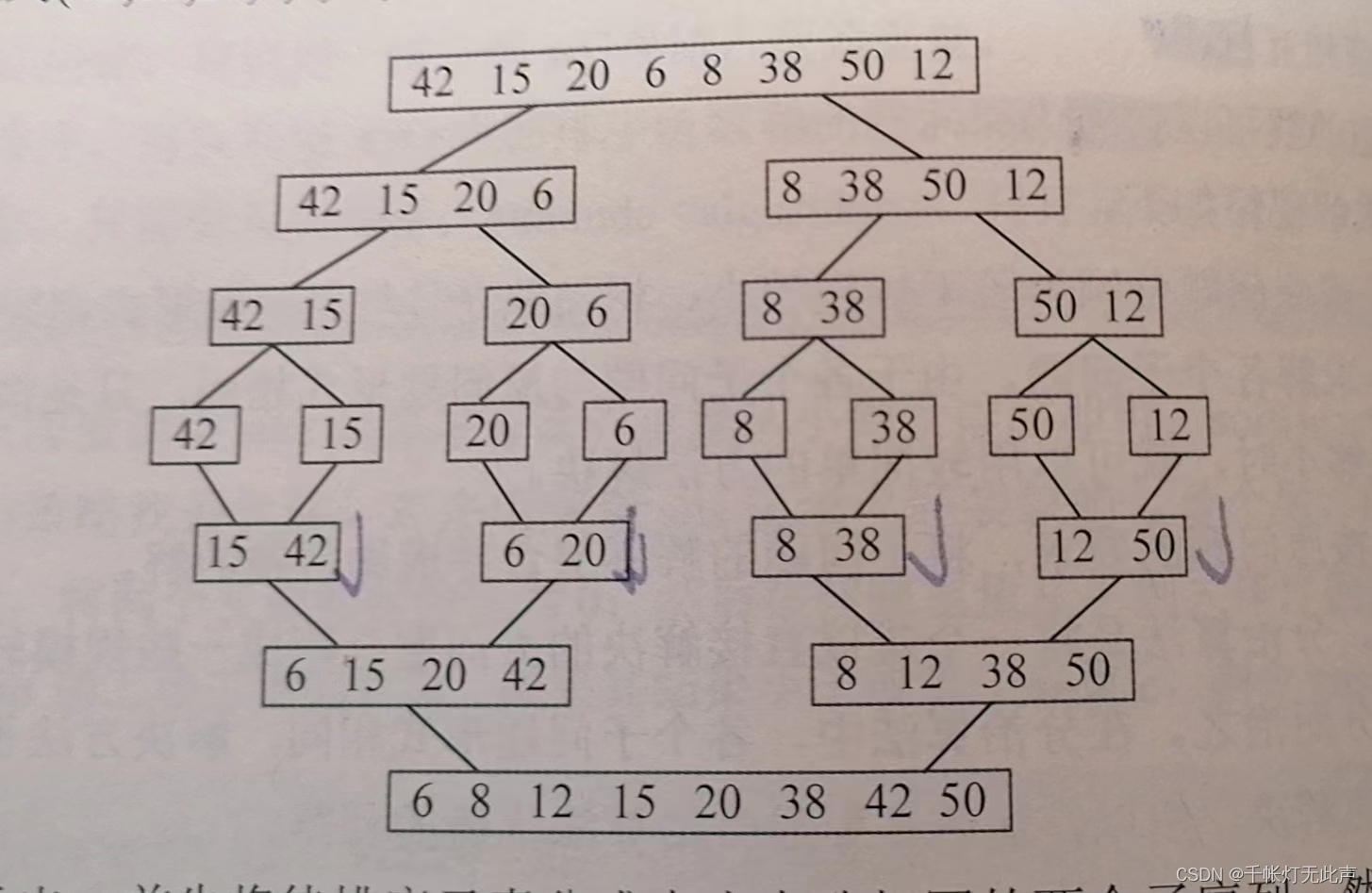
上图，先将待排序元素分成大小相等的的两个子序列

直到分解成一个元素，此时含有一个元素的子序列是有序的

然后，执行合并操作，将两个有序的子序列合并为一个有序序列

直到所有元素都合并完

算法设计

1）合并操作

注意，合并操作执行的只是整个数组排序中的一小步，通过Merge()函数实现

引入辅助合并函数Merge(A, low, mid, high)

函数对两个排好序的子序列A[low:mid]和A[mid + 1:high]进行合并

low, high表示待合并两个子序列在数组中的下界和上界，mid为中间位置

此外，还有3个工作指针i, j, k(整型下标)和辅助数组B

i, j指向两个子序列中，当前待比较的元素，k指向辅助数组B中待放置元素的位置

比较A[i]和A[j]，将较小的值赋值给B[k]，相应指针同时向后移动，直至所有元素处理完毕

初始👇

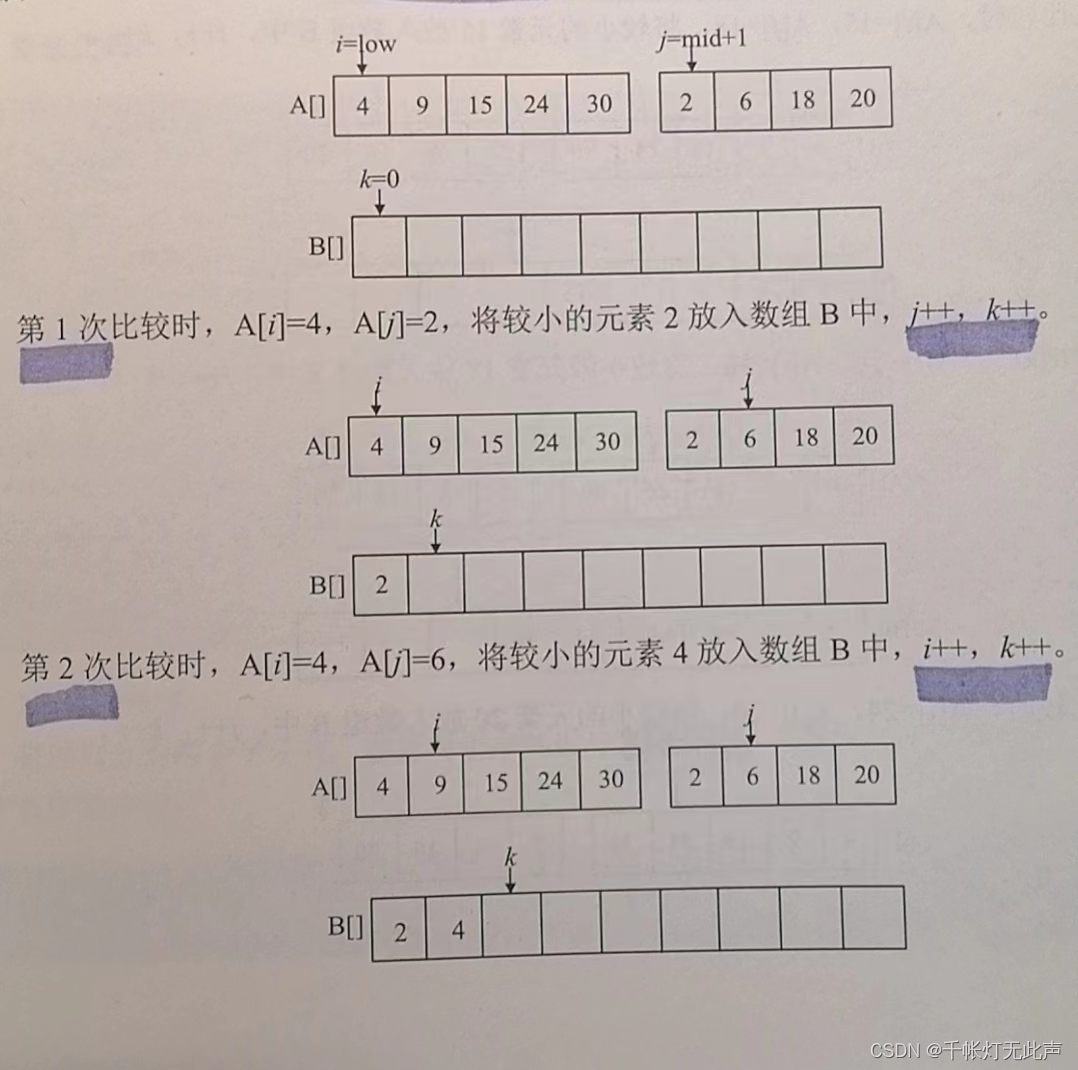
最后👇

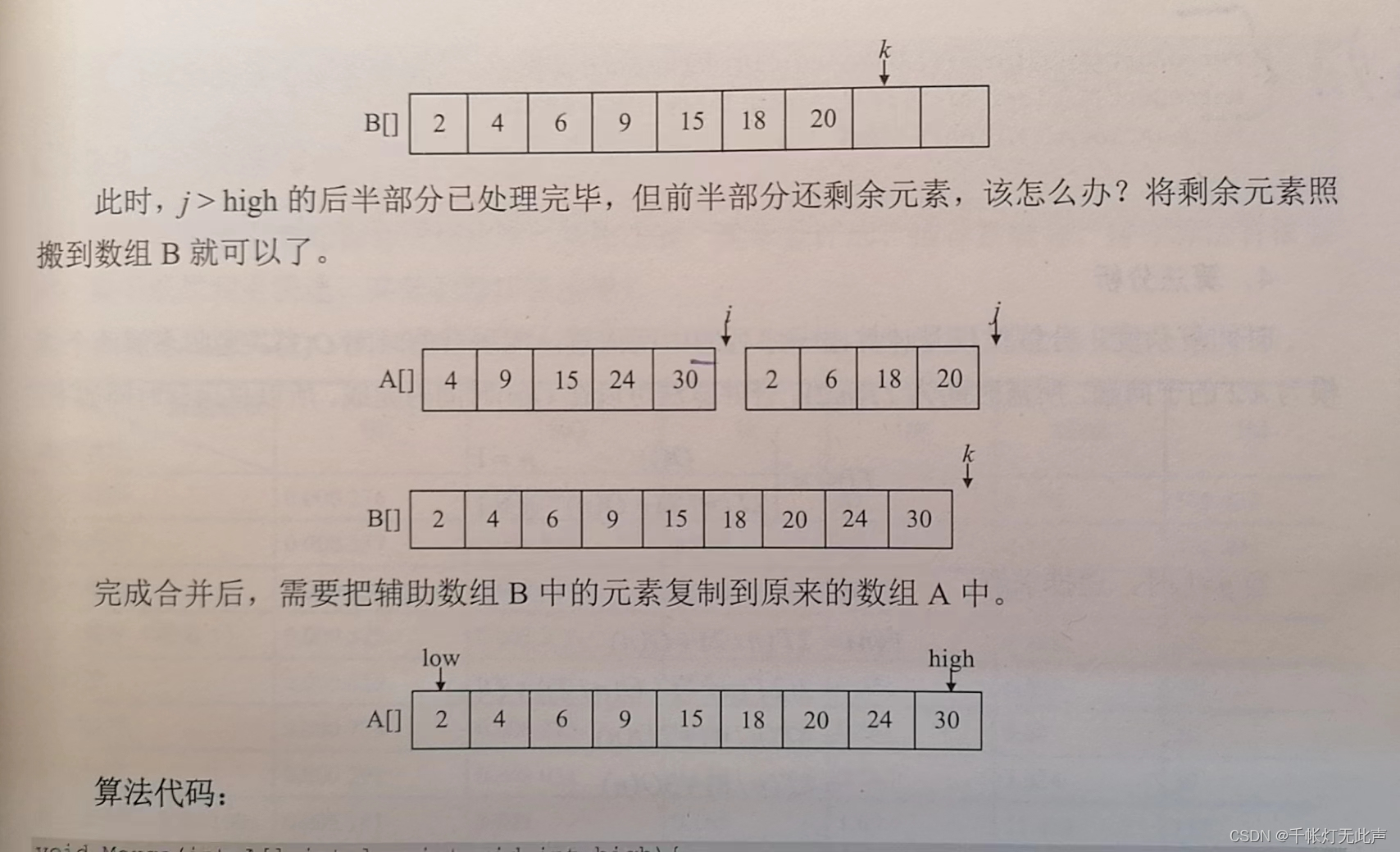
算法代码

void Merge(int A[], int low, int mid, int high) {int *B = new int[high - low + 1]; //申请一个辅助数组int i = low, j = mid + 1, k = 0;while(i <= mid && j <= high) { //从小到达存放到辅助数组B中if(A[i] <= A[j]) B[k++] = A[i++];else B[k++] = A[j++];}while(i <= mid) B[k++] = A[i++]; //数组中剩下元素放到数组B中while(j <= high) B[k++] = A[j++];for(i = low, k = 0; i <= high;++i)A[i] = B[k++];delete[] B;
}

2）合并排序

将序列分成两个子序列，然后对子序列进行递归排序，再把两个已排好序的子序列合并成一个有序的序列

void MergeSort(int A[], int low, int high) {if(low < high) {int mid = (low + high) / 2; //取中点//接下来两行递归MergeSort(A, low, mid); //对A[low:mid]中元素合并排序MergeSort(A, mid + 1, high); //对A[mid+1:high]中元素合并排序Merge(A, low, mid, high); //合并}
}

3）复杂度分析

分解：仅仅计算出子序列中间位置，需要常数时间O(1)

递归：递归求解2个规模为n/2的子问题，需要时间2T(n/2)

合并：需要O(n)

讲的还是很清楚，至于空间复杂度

程序中变量占用了一些辅助空间，这些辅助空间都是常数阶的，但每调用一个Merge()，都分配一个适当大小的缓冲区，在退出时释放，最多分配的大小为n

所以空间复杂度为O(n)，递归调用所使用栈空间等于递归树深度

递归调用的底层元素个数为1，So，n = 2^x，x = logn，递归树深度为logn

🥇2.3.3 快速排序

以前学过了，下面适当补充，放一篇第一天来到csdn的博客

C++快速排序之整型数组_c++整数排序_千帐灯无此声的博客-CSDN博客

排序中

比较慢的有冒泡，选择，插入排序，100万数据量，需要≈15小时

比较快的有希尔，堆，归并，快速，基数排序，100万数据，≈10秒

快排归并对比

1，快排稳定性没有归并排序高

2，但快排是最快的，而且空间复杂度O(1)，而归并O(n)

3，快排：先整体有序，再局部有序 ———— 归并：先局部有序，再整体有序（对比请看图）

快排先整体

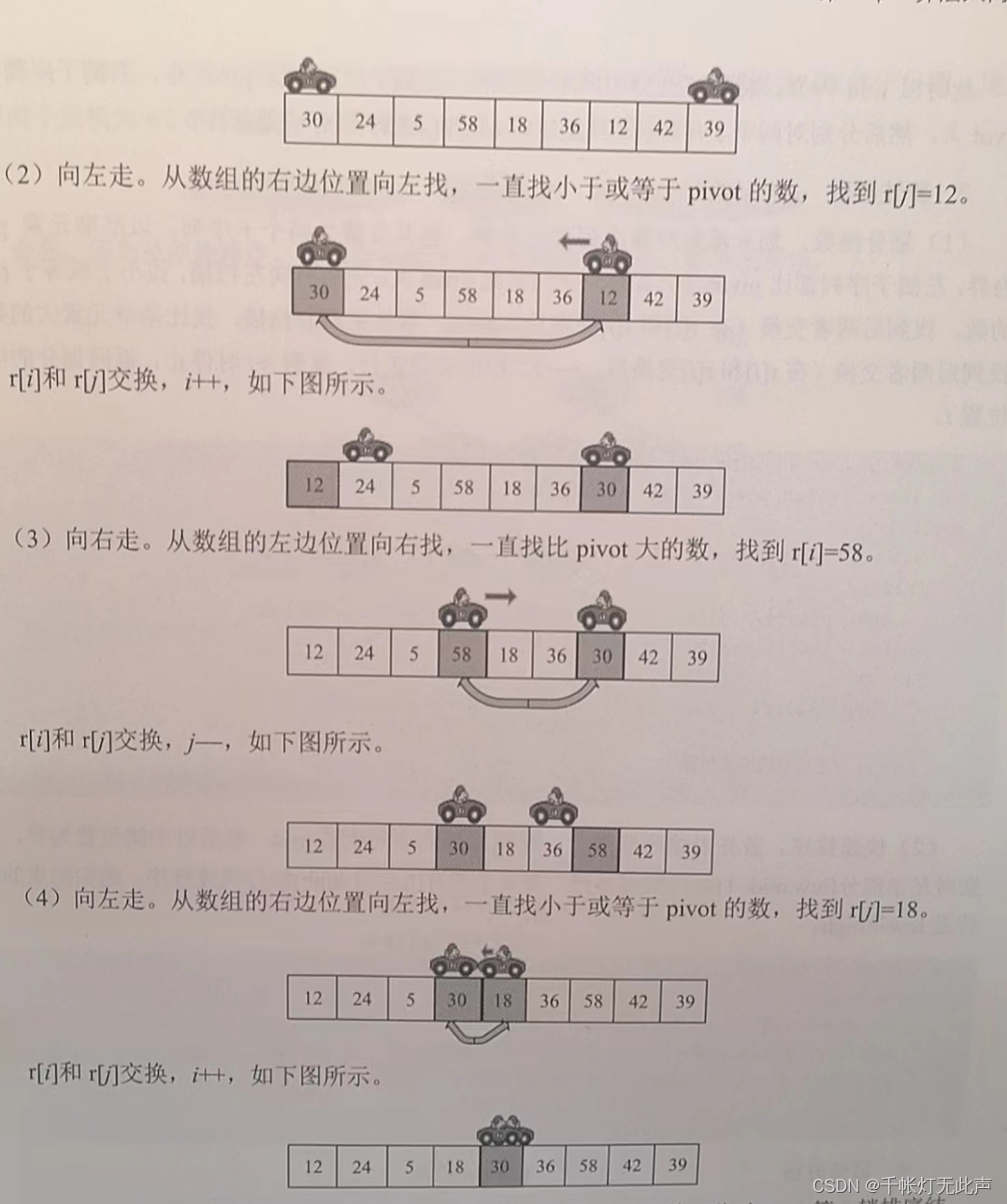
归并先局部

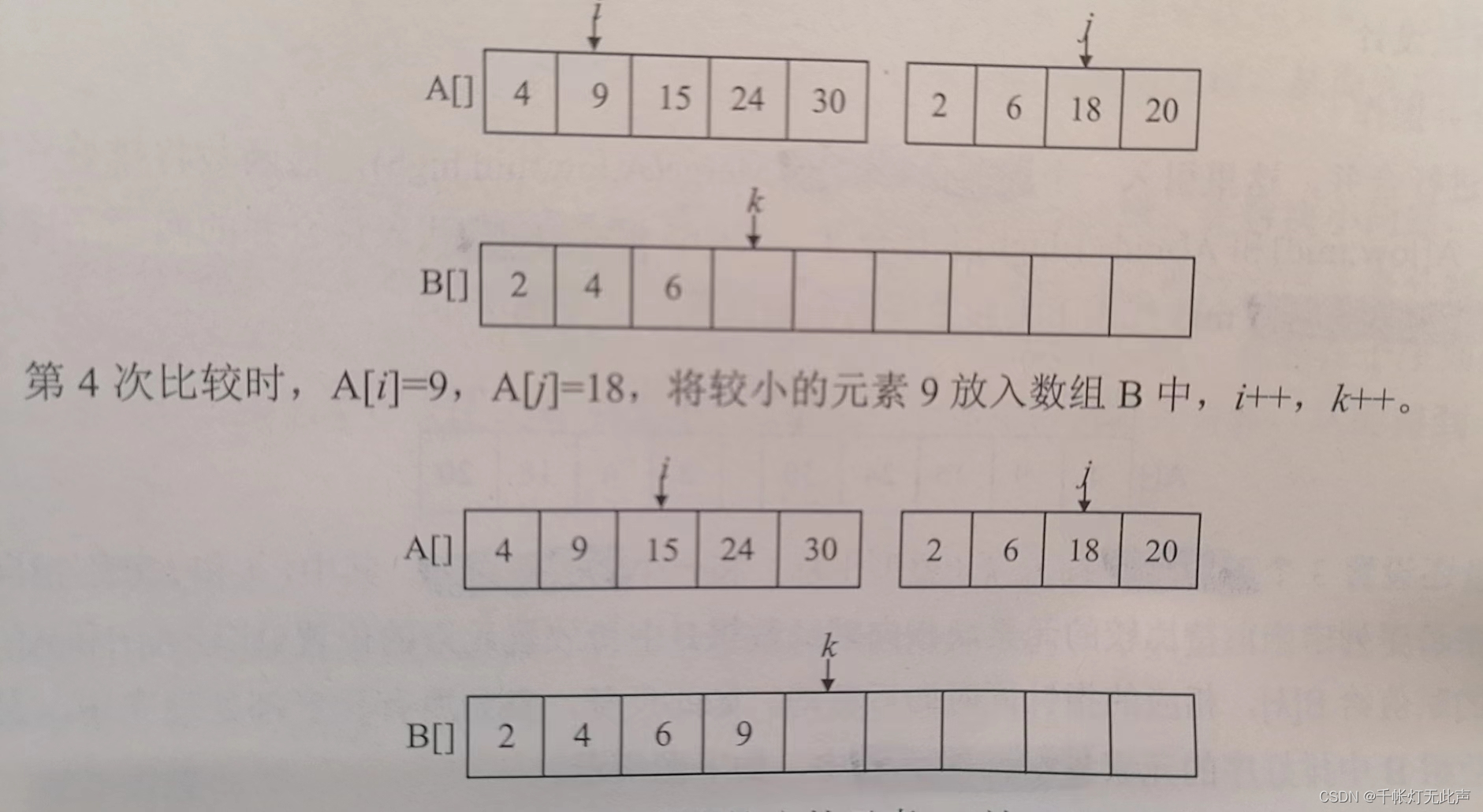
基本思想

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据小，然后分别对两部分进行快速排序

整个排序过程可以递归进行，已达到有序序列

放个以前的代码

#include<iostream>
using namespace std;void Quick_sort(int left, int right, int arr[])
{if(left >= right)return;//终止条件，左边界下标大于等于右边界，//说明当前数组长度是1或该数组物理不存在，这里是递归出口int i, j, base, temp;i = left, j = right;//根据传入的左右边界声明两个游标base = arr[left];//指定好基数while(i < j)//说明二者没相遇，循环继续执行{while(arr[j] >= base && i < j)j--;//j游标先行，只要j游标指向的数值大于基数，j游标就继续移动while(arr[i] <= base && i < j)i++;//i游标后走，只要i游标指向的数值小于基数,i游标就继续移动if(i < j){//退出上面两个循环后，说明i指向了大于基数的元素，j指向了小于基数的元素temp = arr[i];arr[i] = arr[j];arr[j] = temp;//i,j指向的数值交换}}arr[left] = arr[j];//因为j先行，此时i,j指向的相同元素，必然比基数小arr[j] = base;//所以与左端基数交换Quick_sort(left,i-1,arr);//递归处理当前两个游标左边无序数组Quick_sort(i+1,right,arr);//递归处理当前两个游标右边无序数组
}int main()
{int n;while(cin>>n){int arr[n];//数组初始化必须指定长度，且长度为常量，//不指定长度或长度为变量，都会编译出错for(int i = 0; i < n; i++)cin>>arr[i];//strlen()只是求字符串长度，求不了字符数组和整型数组长度Quick_sort(0, n - 1, arr);for(int i = 0; i < n; i++)//老把for写成whilecout<<arr[i]<<" ";}//第一个应该把全部包起来return 0;
}

书里的快排优化拓展，其实就是我上面的代码内容，也是当前互联网主流的快排代码，如果我先学一遍书里一开始的快排代码，就会得不偿失，思路不够清晰而且复杂度更高

🌼P1010 [NOIP1998 普及组] 幂次方

标签：普及-，数学，分治

P1010 [NOIP1998 普及组] 幂次方 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

关于()和+，记得直接从题目复制，防止自己写错

敲完后复制题目输出，和自己的输出比较

//题目输出
//自己输出
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
2(2(2+2(0))+2++2(2(2+2(0))++2(2(2)+2(0))+2+2(0))

第一次显然是有问题的，花15分钟debug

AC 代码

#include<iostream>
#include<cmath> //pow()
using namespace std;void part(int n)
{for(int i = 15; i >= 0; --i) { //2*10^4 < 2^15if(n >= pow(2, i)) {if(i == 0) cout<<"2(0)"; //递归底部else if(i == 1) cout<<"2"; //递归底部else if(i == 2) cout<<"2(2)"; //递归底部else {cout<<"2(";part(i); //递归实现分治cout<<")"; //当前分治完成, 不需要加判断}n -= pow(2, i); //先 -= 再判断'+'的输出if(n != 0) cout<<"+"; //递归结束, 此处n != 0}}
}int main()
{int n;cin>>n;part(n);return 0;
}