目录
- 2.4.4单链表的查找操作(默认带头节点,不带头节点后续更新)
- 2.4.4.1 按位查找操作
- 2.4.4.2 按值查找操作
- 2.4.4.3 求单链表的长度(带和不带头节点都写了)
- 2.4.4.4 知识回顾与重要考点
- 2.4.5 单链表的创建操作
- 2.4.5.1 头插法建立单链表
- 2.4.5.2 尾插法建立单链表
- 2.4.5.3 链表的逆置
2.4.4单链表的查找操作(默认带头节点,不带头节点后续更新)
2.4.4.1 按位查找操作
GetElem(L, i): 按位查找操作,获取表L中第i个位置的元素的值;
LNode * GetElem(LinkList L, int i){if(i<0) return NULL;LNode *p; //指针p指向当前扫描到的结点int j=0; //当前p指向的是第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)while(p!=NULL && j<i){ //循环找到第i个结点p = p->next;j++;}return p; //返回p指针指向的值
}- 注意:
- 1.边界情况 i=0,返回头节点;i>L.length,返回null;
- 2.j<i即查找到j = i 的节点,就是第i个节点。
- 3.平均复杂度O(n)
2.4.4.2 按值查找操作
LocateElem(L, e):按值查找操作,在表L中查找具有给定关键字值的元素;
平均复杂度O(n)
LNode * LocateElem(LinkList L, ElemType e){LNode *P = L->next; //p指向第一个结点//从第一个结点开始查找数据域为e的结点while(p!=NULL && p->data != e){p = p->next;}return p; //找到后返回该结点指针,否则返回NULL
}2.4.4.3 求单链表的长度(带和不带头节点都写了)
Length(LinkList L) :计算单链表中数据结点**(不含头结点)的个数**,需要从第一个结点看是顺序依次访问表中的每个结点。算法的时间复杂度为O(n)。
带头节点:
int Length(LinkList L){int len=0; //统计表长LNode *p = L;while(p->next != NULL){ //只有指向的下一个节点不为null,才len++p = p->next;len++;}return len;
}不带头节点:
int Length(LinkList L){int len=0; //统计表长LNode *p = L;while(p!= NULL){ //当前指针(即头节点指向的第一个节点)不为空即可++,//带头节点的链表用这种方法长度会算上头节点。p = p->next;len++;}return len;
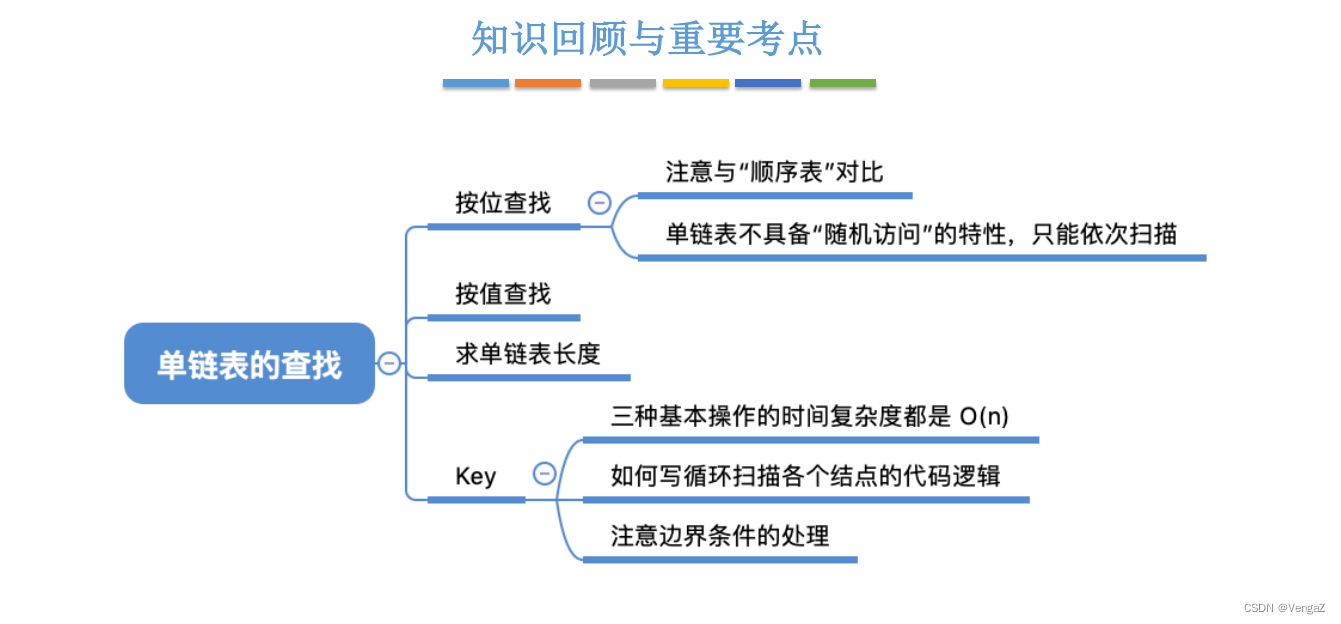
}2.4.4.4 知识回顾与重要考点
2.4.5 单链表的创建操作
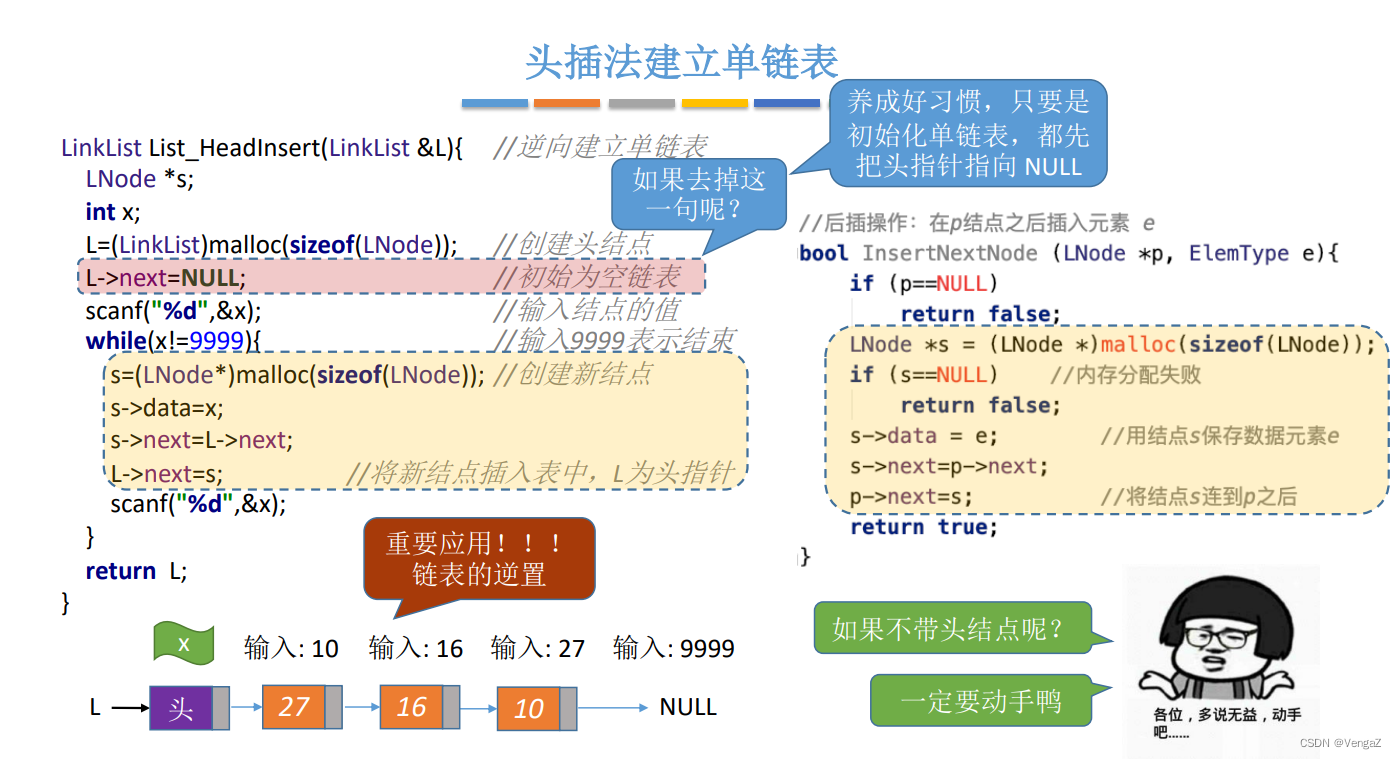
2.4.5.1 头插法建立单链表
带头节点;
若不带头节点,头插法就是插入头指针指向的第一个节点
平均时间复杂度O(n)
思路:每次都将生成的结点插入到链表的表头。
LinkList List_HeadInsert(LinkList &L){ //逆向建立单链表LNode *s;int x;L = (LinkList)malloc(sizeof(LNode)); //建立头结点L->next = NULL; //初始为空链表,这步不能少!scanf("%d", &x); //输入要插入的结点的值while(x!=9999){ //输入9999表结束s = (LNode *)malloc(sizeof(LNode)); //创建新结点s->data = x;s->next = L->next;L->next = s; //将新结点插入表中,L为头指针scanf("%d", &x); }return L;}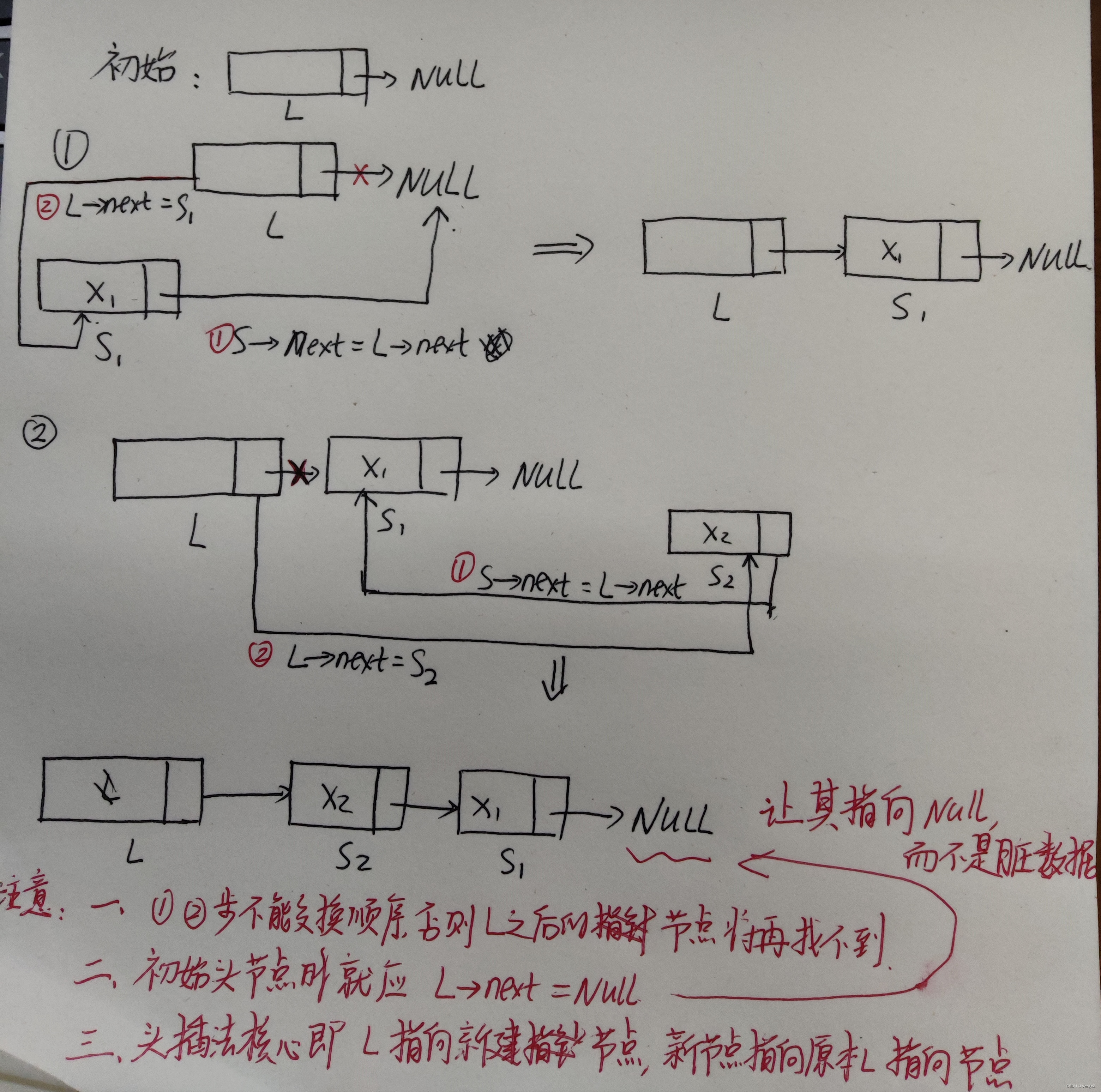
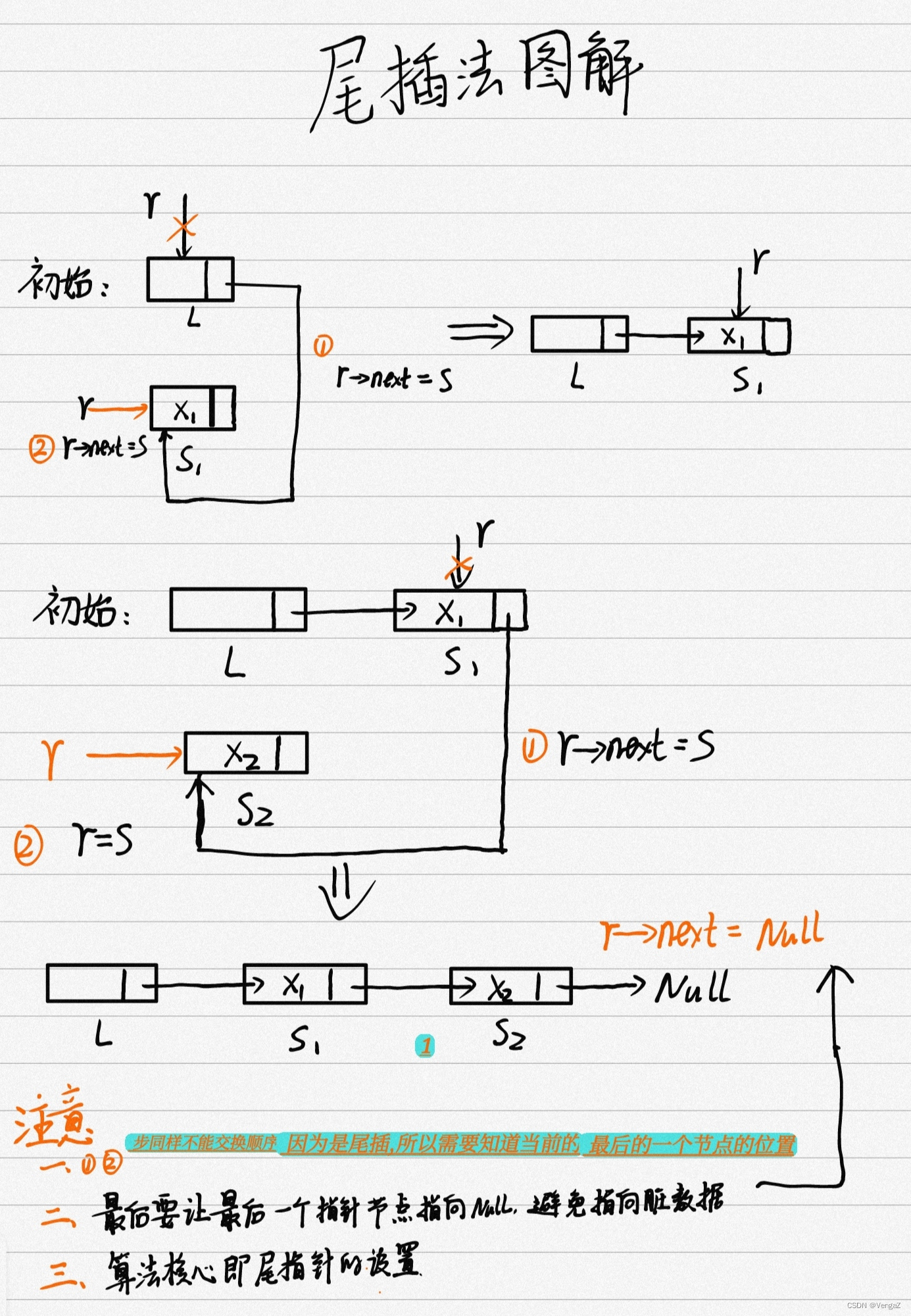
2.4.5.2 尾插法建立单链表
带头节点;
若不带头节点则需要特殊处理第一次插入数据的情况,是直接赋值而不是对下一个节点赋值。
时间复杂度O(n)
思路:每次将新节点插入到当前链表的表尾,所以必须增加一个尾指针r,使其始终指向当前链表的尾结点。
好处:生成的链表中结点的次序和输入数据的顺序会一致。
LinkList List_TailInsert(LinkList &L){ //正向建立单链表int x; //设ElemType为整型intL = (LinkList)malloc(sizeof(LNode)); //建立头结点(初始化空表)LNode *s, *r = L; //r为表尾指针scanf("%d", &x); //输入要插入的结点的值while(x!=9999){ //输入9999表结束s = (LNode *)malloc(sizeof(LNode));s->data = x;r->next = s;r = s //r指针指向新的表尾结点scanf("%d", &x); }r->next = NULL; //尾结点指针置空return L;
}
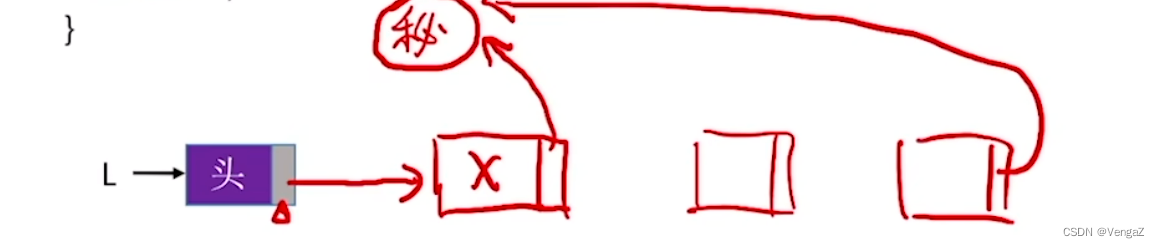
- 注意:
- 头插法和尾插法在初始化的时候
头插法:L = (LinkList)malloc(sizeof(LNode)); //建立头结点L->next = NULL; //初始为空链表,这步不能少!
尾插法:L = (LinkList)malloc(sizeof(LNode)); //建立头结点(初始化空表)r->next = NULL; //尾结点指针置空
都是为了保证最后一个节点指向的不是脏数据,即malloc动态分配空间的时候可能,
指向的是一个脏数据
2.4.5.3 链表的逆置
算法思想:逆置链表初始为空,原表中结点从原链表中依次“删除”,再逐个插入逆置链表的表头(即“头插”到逆置链表中),使它成为逆置链表的“新”的第一个结点,如此循环,直至原链表为空;
带头节点:
void listReverse(linkedList &L)
{node *p,*s;//1.准备工作p = L->next;L->next = NULL;while(p){//2.1 s记录正在处理的结点,p记录下一轮待处理的结点s = p; //s承接上一轮记录的位置p = p->next; //p为下一轮记录位置//2.2 把s插入 已逆置的部分 中s->next = L->next; // L->next代表已逆置的第一结点,s的指针域指向它L->next = s; //(头结点的指针域,即)第一结点 设置为s//2.2步骤相当于://s 对 队伍(已逆置部分)的队首(已逆置的第一结点)说:你不要排在柜台前了,你排在我后面//等队伍排在s后面后,s自己排到了柜台前}
}讲解
我们先看第一轮循环做了什么:
阅读顺序:黑色(初始)、蓝色(操作)、红色(理解)
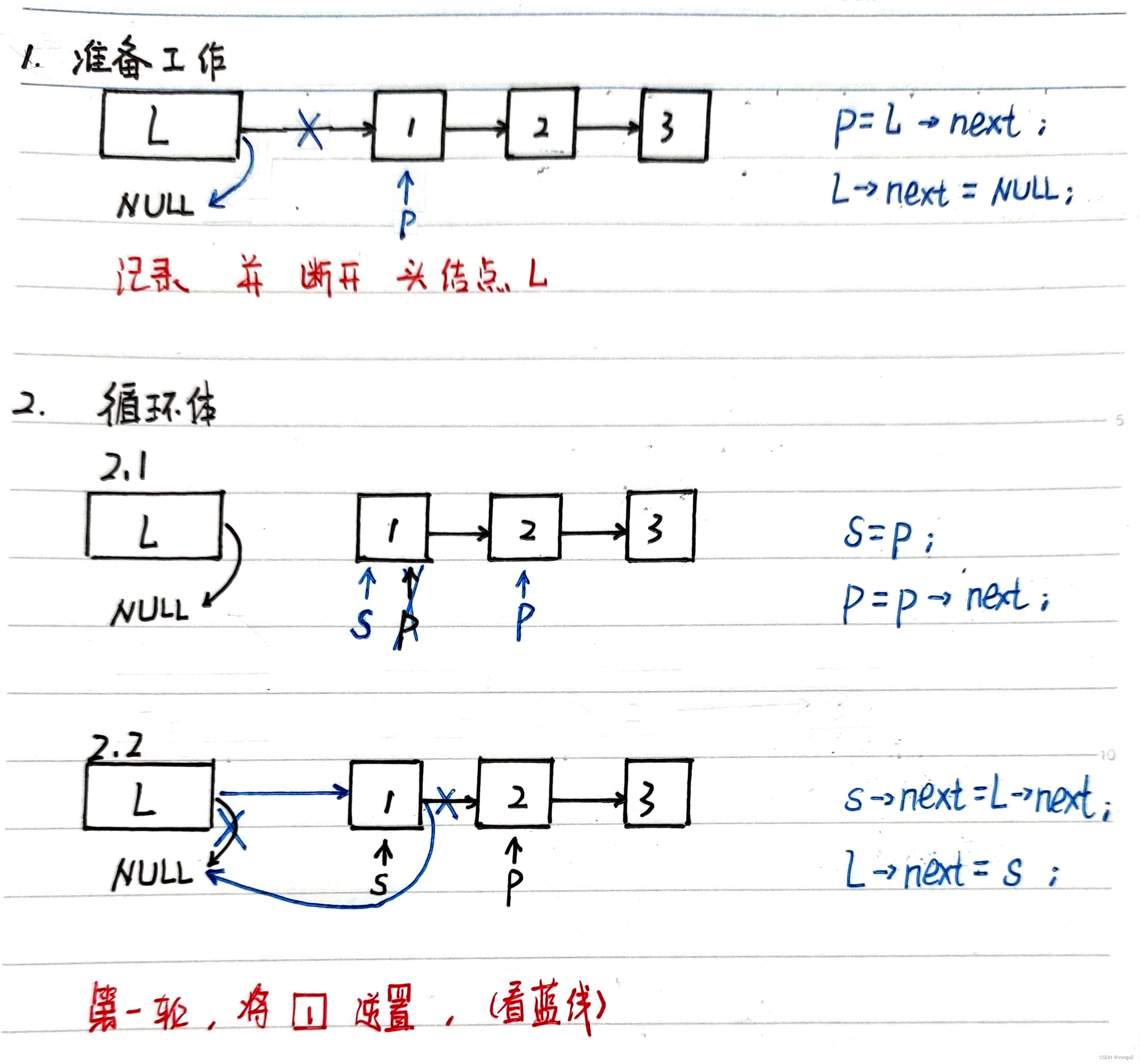
第二轮:
阅读顺序:黑色(初始)、蓝色(操作)、红色(理解)
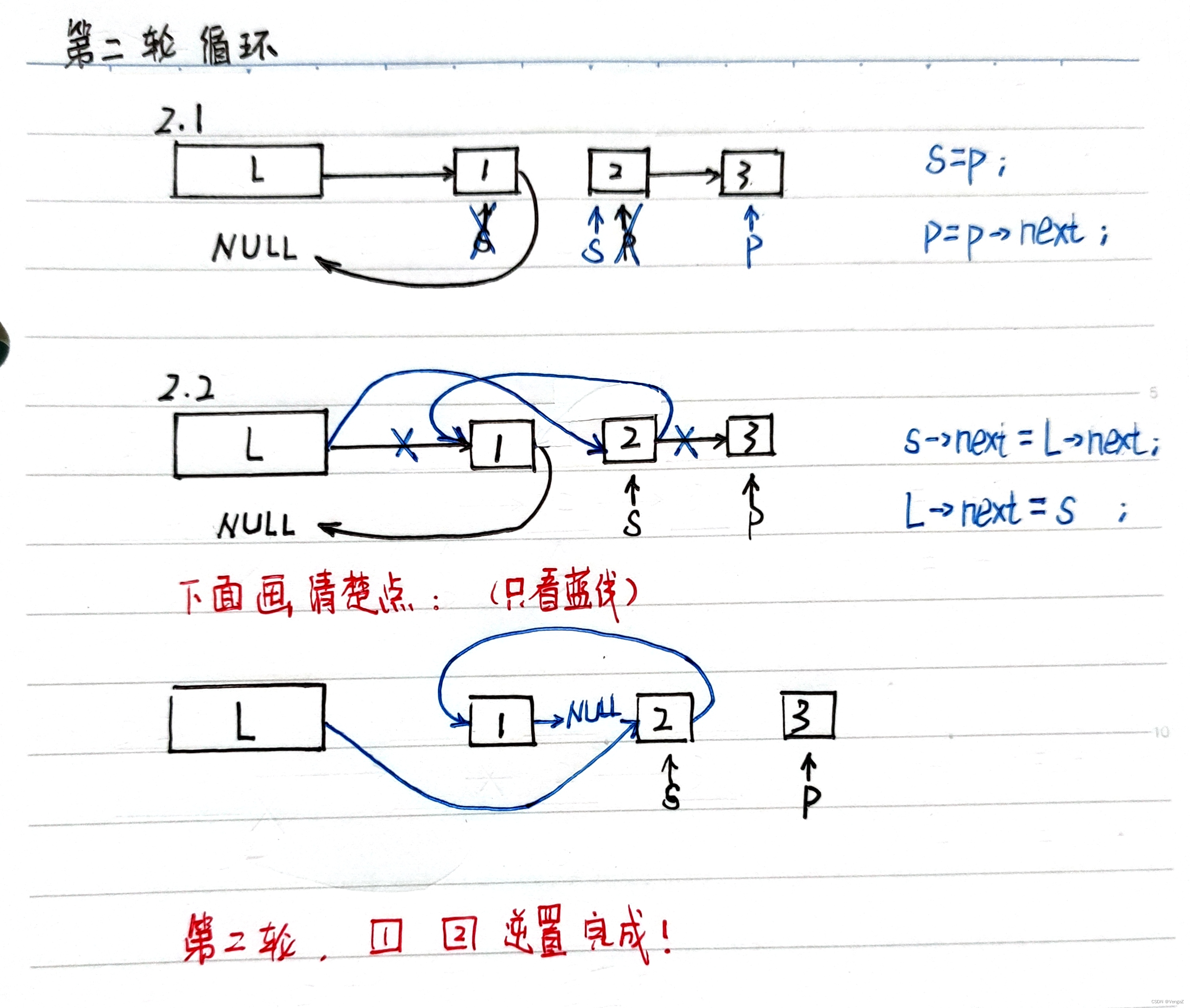
总结
不难发现:
-
链表逆置利用了s、p两个指针的移动实现
每一轮循环体执行结束后,s指向刚刚逆置成功的结点,p指向下一轮待逆置的结点 -
为什么需要p?
因为2.2步骤中s->next会被改写,
若只有s,会丢失剩余的结点,
这时候p起到暂存的作用,等待下一轮2.1步骤中的s=p找到它。