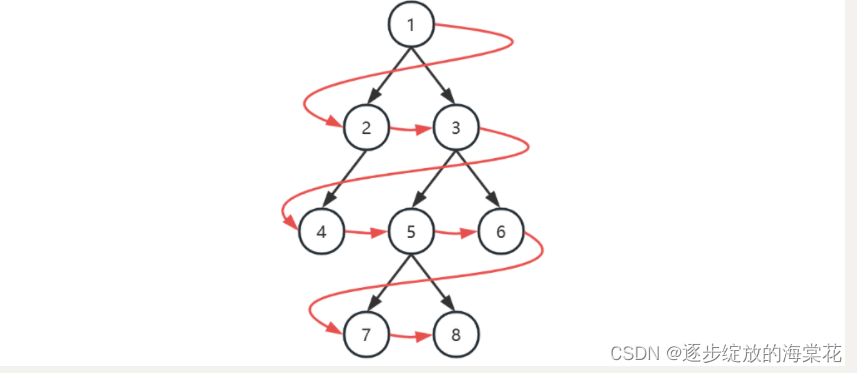
二叉树是这么一种树状结构：每个节点最多有两个孩子，左孩子和右孩子

重要的二叉树结构

• 完全二叉树（complete binary tree）是一种二叉树结构，除最后一层以外，每一层都必须填满，填充时要遵从先左后右

• 平衡二叉树（balance binary tree）是一种二叉树结构，其中每个节点的左右子树高度相差不超过 1

1、存储

存储方式分为两种

1. 定义树节点与左、右孩子引用（TreeNode）

2. 使用数组，前面讲堆时用过，若以 0 作为树的根，索引可以通过如下方式计算

   • 父 = floor((子 - 1) / 2)

   • 左孩子 = 父 * 2 + 1

   • 右孩子 = 父 * 2 + 2

二叉树的节点结构

/*** 二叉树节点** @author zjj_admin*/
public class TreeNode {int val;TreeNode left;TreeNode right;
​public TreeNode(int val) {this.val = val;}
​public TreeNode(TreeNode left, int val, TreeNode right) {this.left = left;this.val = val;this.right = right;}
}

2、遍历

遍历也分为两种

1. 广度优先遍历（Breadth-first order）：尽可能先访问距离根最近的节点，也称为层序遍历

2. 深度优先遍历（Depth-first order）：对于二叉树，可以进一步分成三种（要深入到叶子节点）

   1. pre-order 前序遍历，对于每一棵子树，先访问该节点，然后是左子树，最后是右子树

   2. in-order 中序遍历，对于每一棵子树，先访问左子树，然后是该节点，最后是右子树

   3. post-order 后序遍历，对于每一棵子树，先访问左子树，然后是右子树，最后是该节点

2.1、广度优先

 

本轮开始时队列	本轮访问节点
[1]	1
[2, 3]	2
[3, 4]	3
[4, 5, 6]	4
[5, 6]	5
[6, 7, 8]	6
[7, 8]	7
[8]	8
[]

1. 初始化，将根节点加入队列

2. 循环处理队列中每个节点，直至队列为空

3. 每次循环内处理节点后，将它的孩子节点（即下一层的节点）加入队列

注意

• 以上用队列来层序遍历是针对 TreeNode 这种方式表示的二叉树

• 对于数组表现的二叉树，则直接遍历数组即可，自然为层序遍历的顺序

2.2、深度优先遍历

深度优先遍历有前序遍历、中序遍历和后续遍历三种

1. 前序遍历: 先输出父节点，再遍历左子树和右子树

2. 中序遍历: 先遍历左子树，再输出父节点，再遍历右子树

3. 后序遍历: 先遍历左子树，再遍历右子树，最后输出父节点

• 小结: 看输出父节点的顺序，就确定是前序，中序还是后序

前，中，后序遍历详解

1. 创建一颗二叉树

2. 前序遍历 2.1 先输出当前节点(初始的时候是root节点) 2.2 如果左子节点不为空，则递归继续前序遍历 2.3 如果右子节点不为空，则递归继续前序遍历

3. 中序遍历 3.1 如果当前节点的左子节点不为空，则递归中序遍历 3.2 输出当前节点 3.3 如果当前节点的右子节点不为空，则递归中序遍历

4. 后序遍历 4.1 如果当前节点的左子节点不为空，则递归后序遍历 4.2 如果当前节点的右子节点不为空，则递归后序遍历 4.3 输出当前节点

2.3、递归实现深度优先遍历

/*** 前序遍历，继续递归实现** @param root*/
static void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + "\t");preOrder(root.left);preOrder(root.right);
}
​
​
/*** 中序遍历** @param root*/
static void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + "\t");inOrder(root.right);
}
​
​
/*** 后续遍历** @param root*/
static void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + "\t");
}

2.4、非递归实现深度优先遍历

   /*** 前序遍历* 使用非递归的方式** @param root*/static String preOrder(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList();StringBuilder res = new StringBuilder();TreeNode curr = root;while (curr != null || !stack.isEmpty()) {if (curr != null) {res.append(curr.val).append(" ");stack.push(curr);curr = curr.left;} else {//弹栈TreeNode pop = stack.pop();curr = pop.right;}}return res.toString();}
​
​/*** 中序遍历* 使用非递归的方式** @param root*/static String inOrder(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList();StringBuilder res = new StringBuilder();TreeNode curr = root;while (curr != null || !stack.isEmpty()) {if (curr != null) {stack.push(curr);curr = curr.left;} else {//弹栈TreeNode pop = stack.pop();res.append(pop.val).append(" ");curr = pop.right;}}return res.toString();}
​
​/*** 后续遍历* 使用非递归的方式** @param root*/static String postOrder(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList();StringBuilder res = new StringBuilder();TreeNode curr = root;TreeNode pop = null;while (curr != null || !stack.isEmpty()) {if (curr != null) {stack.push(curr);curr = curr.left;} else {TreeNode peek = stack.peek();if (peek.right == null || peek.right == pop) {//弹栈pop = stack.pop();res.append(pop.val).append(" ");} else {curr = peek.right;}}}return res.toString();}

2.5、在一个方法中实现二叉树的三种深度优先遍历（前序、中序和后续）

/*** 使用非递归的方式求解，在一个方法中实现* 实现前序遍历，中序遍历和后续遍历** @param root*/
static List<String> order(TreeNode root) {TreeNode curr = root;StringBuilder pre = new StringBuilder("preOrder:");StringBuilder in = new StringBuilder("inOrder:");StringBuilder post = new StringBuilder("postOrder:");//定义一个栈，用于存储当前节点的父节点LinkedList<TreeNode> s = new LinkedList();TreeNode pop = null;while (curr != null || !s.isEmpty()) {if (curr != null) {s.push(curr);pre.append(curr.val + " ");//依次向左边遍历curr = curr.left;} else {TreeNode peek = s.peek();if (peek.right == null) {in.append(peek.val + " ");//当没有右节点时pop = s.pop();//这一行打印的是中序遍历的结果post.append(pop.val + " ");} else if (peek.right == pop) {//当右节点已经遍历结束时pop = s.pop();//这一行打印的是中序遍历的结果post.append(pop.val + " ");} else {//右节点不为空并且没有遍历in.append(peek.val + " ");curr = peek.right;}}}return List.of(pre.toString(), in.toString(), post.toString());
}