目录
🌴时间复杂度练习
📌面试题--->消失的数字
题目描述
题目链接:面试题 17.04. 消失的数字
🌴解题思路
📌思路1:
malloc函数用法
📌思路2:
📌思路3:
🌴时间复杂度练习
🙊 如果有不了解时间复杂度的请移步上一篇文章:【数据结构】初识
📌面试题--->消失的数字
题目描述
数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
题目链接:面试题 17.04. 消失的数字
示例 1:
输入:
[3,0,1]输出:
2示例 2:
输入:
[9,6,4,2,3,5,7,0,1] 输出:
8🌴解题思路
📌思路1:
1.开辟一个额外的N+1个数的数组(即malloc一个额外N+1个数的数组),建立一个映射关系,,将数组的值全部初始化为-1
2.遍历这些数字,这个数是多少就写到数组的对应位置
3.再遍历一遍数组,哪个位置是-1,哪个位置的下表就是缺失的数字
因为malloc数组基本没有时间消耗,但是初始化时需要循环N+1次,填数字的时候也循环了N+1次,最后遍历时最坏也要循环N+1次,总共3N+3次,根据大O的渐进表示法就知道时间复杂度O(N)。
时间复杂度是:O(N)
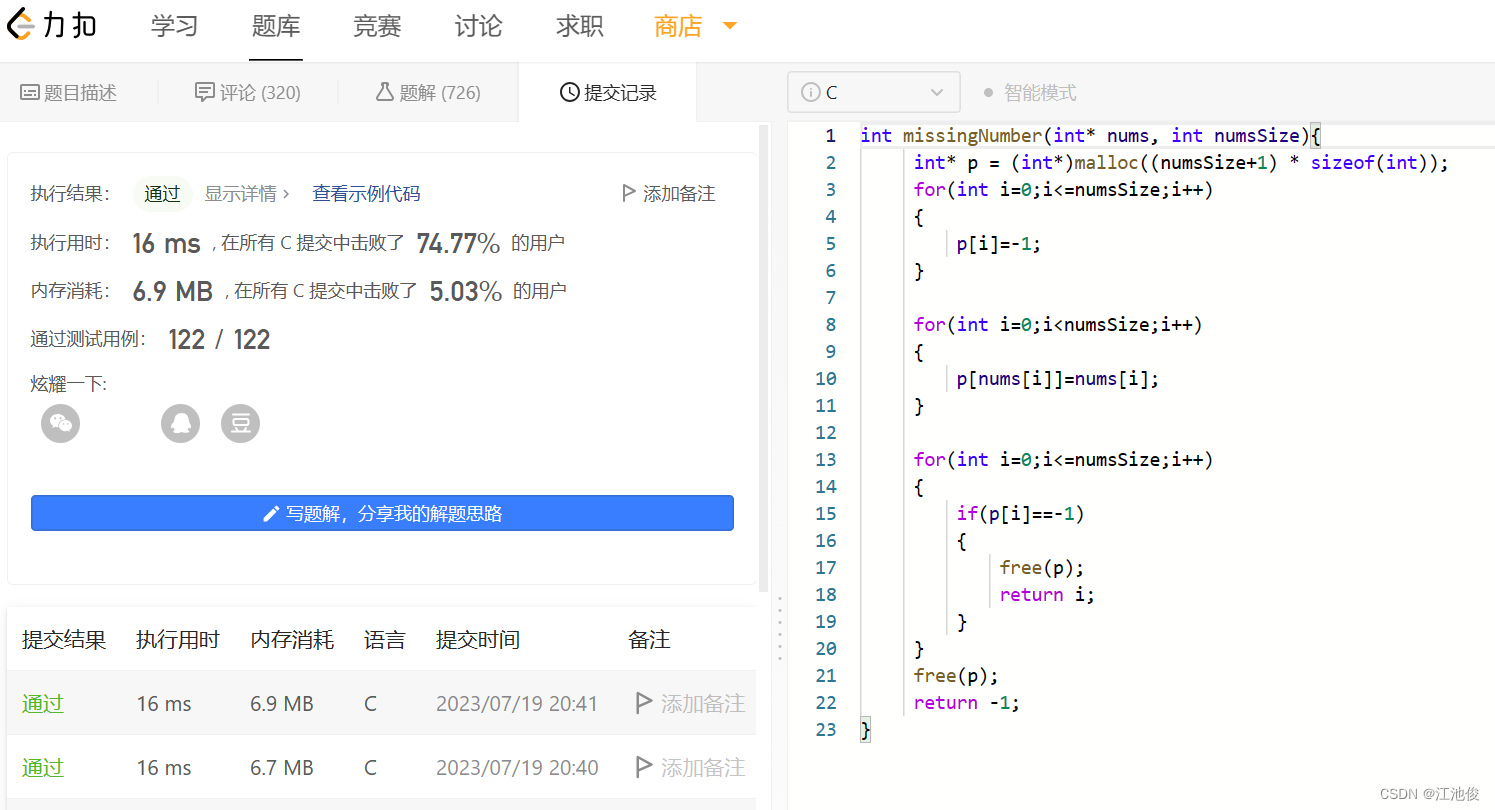
代码展示:
int missingNumber(int* nums, int numsSize){int* p = (int*)malloc((numsSize+1) * sizeof(int));for(int i=0;i<=numsSize;i++){p[i]=-1;}for(int i=0;i<numsSize;i++){p[nums[i]]=nums[i];}for(int i=0;i<=numsSize;i++){if(p[i]==-1){free(p);return i;}}free(p);return -1;
}结果:
malloc函数用法
函数声明:
void *malloc(size_t size)头文件: <stdlib.h>
参数:
size --- 内存块的大小,以字节为单位。
返回值:
该函数返回一个指针 ,指向已分配大小的内存。为避免内存泄漏,必须用 free() 或 realloc() 解分配返回的指针。如果请求失败,则返回 NULL。
示例:
double * pt;
pt = (double * ) malloc (30 * sizeof(double));
这段代码请求30个double类型值的空间,并且让pt指向该空间所在位置。
在释放空间时只需如下操作:
free(pt);📌思路2:
异或:------>符号:^
用一个 x = 0,x跟数组中的这些数据都异或一遍,
然后再跟0-N之间的数字异或一遍,最后x才是缺失的数字。
注意:❗️0^x = x ❗️ a^a = 0
❗️异或满足交换律和结合律(即1^2^3^1^2 = 1^1^2^2^3 =3)
因为第一遍异或时需要循环N次,第二遍也需要N次,总共2N次,根据大O的渐进表示法就知道时间复杂度为O(N)。
时间复杂度:O(N)
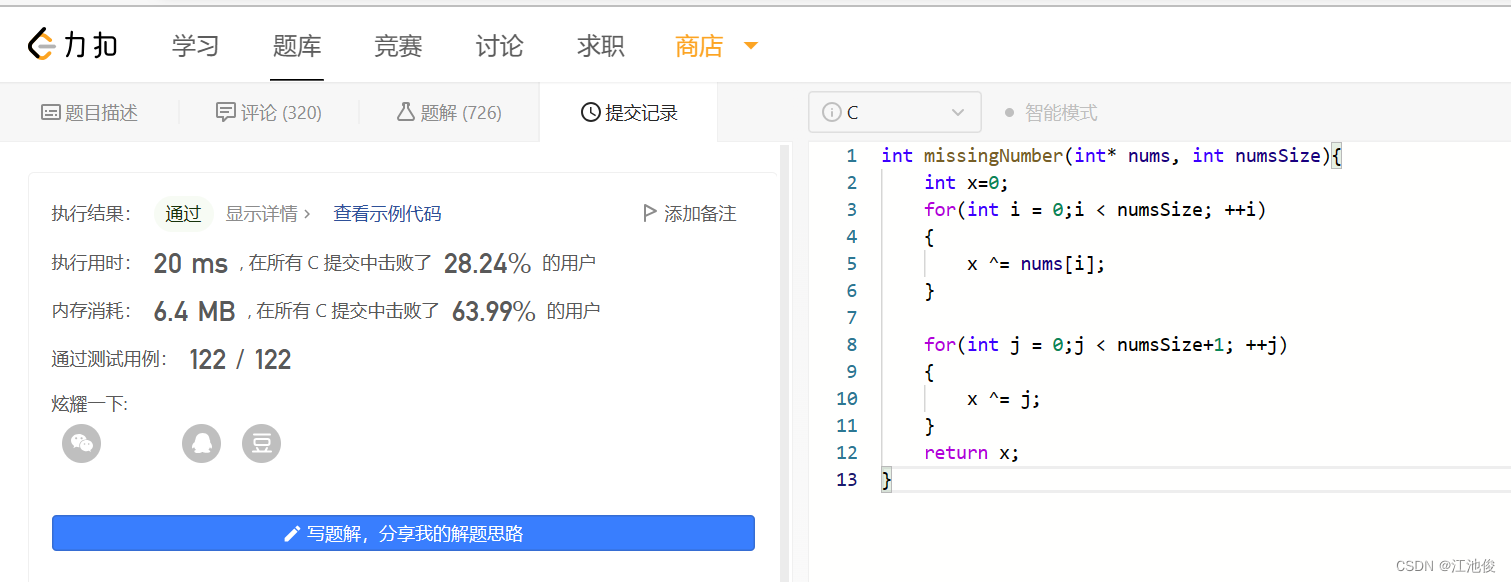
代码展示:
int missingNumber(int* nums, int numsSize){int x=0;for(int i = 0;i < numsSize; ++i){x ^= nums[i];}for(int j = 0;j < numsSize+1; ++j){x ^= j;}return x;
}注意: 这里* nums表示存放0-N中缺失了一个数字后的所有数字的数组,一共有numsSize个,而0-N之间一共有numsSize+1个数。
结果:
📌思路3:
公式计算:
1.求0-N这些数的和(利用求和公式)
2.再求数组中存放的这些数的和(用for循环)
3.将第一次求的和减去第二次求的和即为缺失的数字
因为第一次求和使用公式所以基本不消耗时间,第二次求和进行了N次循环,总共N次,根据大O的渐进表示法就知道时间复杂度为O(N)。
时间复杂度:O(N)
代码展示:
int missingNumber(int* nums, int numsSize){
int sum = ((numsSize + 1) * numsSize) / 2;
for (int i = 0;i< numsSize; ++i)
{sum -=*(nums+i);
}
return sum;
}结果:
🔥今天的分享就到这里,如果觉得博主的文章还不错的话,请👍三连支持一下博主哦🤞