✅<1>主页:我的代码爱吃辣
📃<2>知识讲解:数据结构——二叉树
🔥<3>创作者:我的代码爱吃辣
☂️<4>开发环境:Visual Studio 2022
💬<5>前言:上期讲了二叉树的顺序存储,今天来讲一下二叉树的链式存储。
目录
一.结点创建:
二.二叉树的遍历:
(1)前序,中序,以及后序遍历
2.中序遍历
3.后序遍历
二.二叉树的层序遍历
三.二叉树节点数
四. 叶子结点数
五.最大高度
六.查找二叉树结点
七.二叉树的销毁
八.二叉树的创建
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
一.结点创建:
typedef int BTDatetype;
//二叉树结点
typedef struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
}BTNode;//结点的创建
BTNode* BTBuyNode(int val)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->val = val;node->right = node->left = NULL;return node;
}
int main()
{BTNode* n1 = BTBuyNode(1);BTNode* n2 = BTBuyNode(2);BTNode* n3 = BTBuyNode(3);BTNode* n4 = BTBuyNode(4);BTNode* n5 = BTBuyNode(5);BTNode* n6 = BTBuyNode(6);BTNode* n7 = BTBuyNode(7);n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;}注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的。

从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
二.二叉树的遍历:
(1)前序,中序,以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
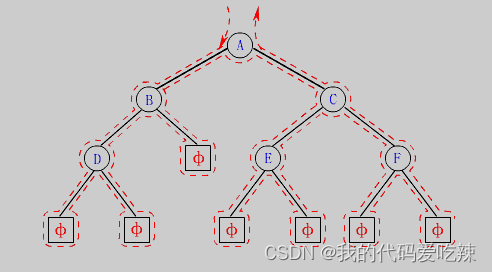
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
1.先序遍历:
访问根结点的操作发生在遍历其左右子树之前,意思就是在每一颗树而言都是,先访问根,在访问左子树,最后访问右子树。
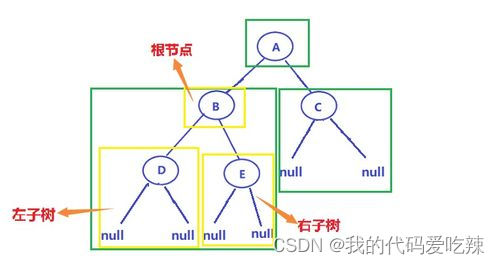
A作为整个树的根,先访问A,紧接着访问左子树,面对左子树也是由根左右构成,所以再访问左子树的根B,在访问B的左子树,以此类推经行递归。
代码:
//前序遍历
void PrevOrder(BTNode* root)
{//如果这棵树是空树,就直接返回if (root == NULL){printf("NULL ");return;}//如果这棵树不是空树,那就先访问根,再递归访问左子树和右子树printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}测试:
int main()
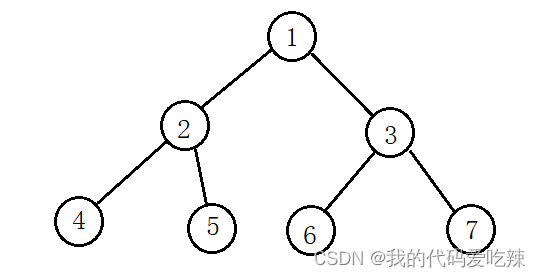
{ //二叉树创建BTNode* n1 = BTBuyNode(1);BTNode* n2 = BTBuyNode(2);BTNode* n3 = BTBuyNode(3);BTNode* n4 = BTBuyNode(4);BTNode* n5 = BTBuyNode(5);BTNode* n6 = BTBuyNode(6);BTNode* n7 = BTBuyNode(7);n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;//前序遍历PrevOrder(n1);return 0;
}

2.中序遍历
中序遍历,在递归思想上和前序遍历一样,唯一的区别就是,前序遍历时先访问根节点,再访问左右子树,而中序遍历是:先访问左子树再访问根节点最后在访问右子树。
代码:
void MidOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}MidOrder(root->left);printf("%d ", root->val);MidOrder(root->right);
}

3.后序遍历
先访问左子树、再访问右子树,最后访问根结点。
代码:
void BankOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BankOrder(root->left);BankOrder(root->right);printf("%d ", root->val);
}

二.二叉树的层序遍历
二叉树的层序遍历,就是从上往下,从左往右,一个一个遍历。
例如:
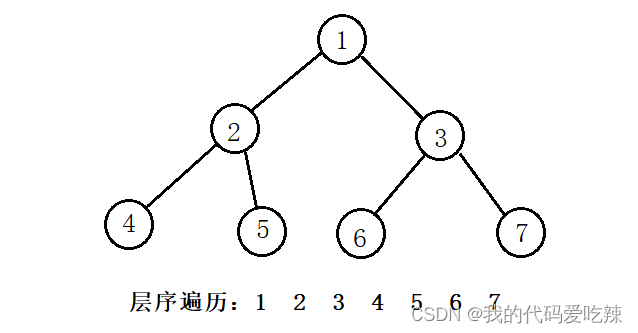
要想达成这样的遍历,我们需要借助队列,主要的操作就是,在结点出队列时,如果他有孩子就将该结点的孩子进队列,一直出队列直到队列为空。
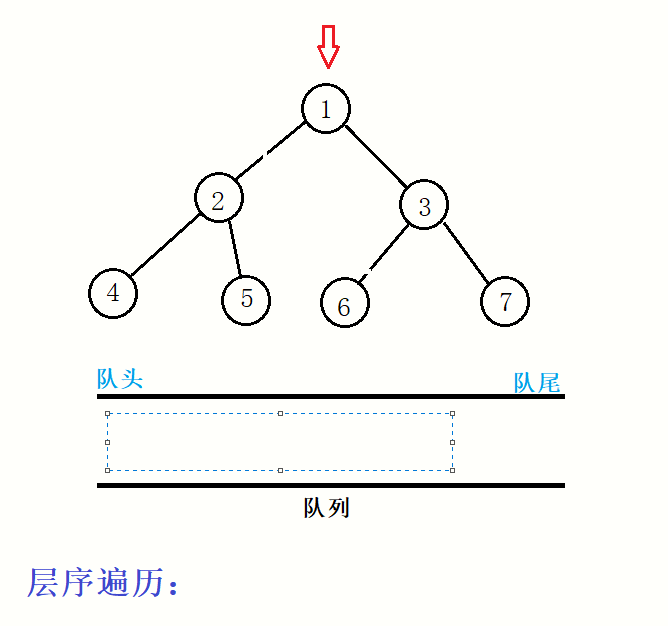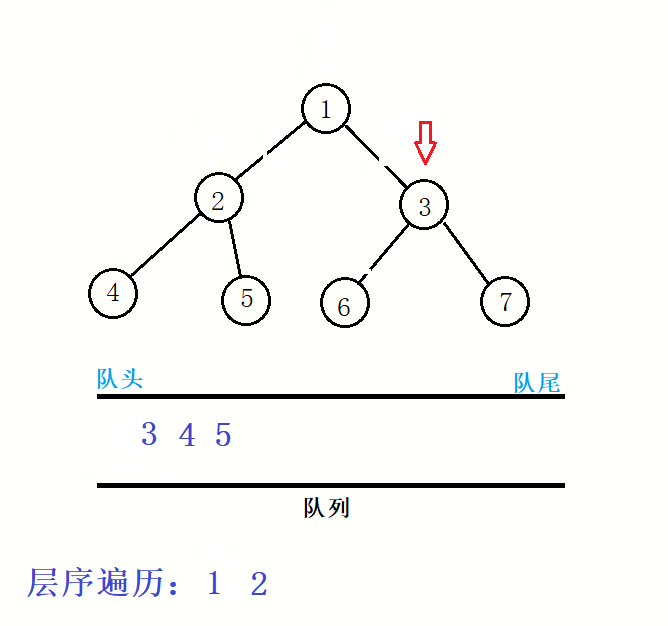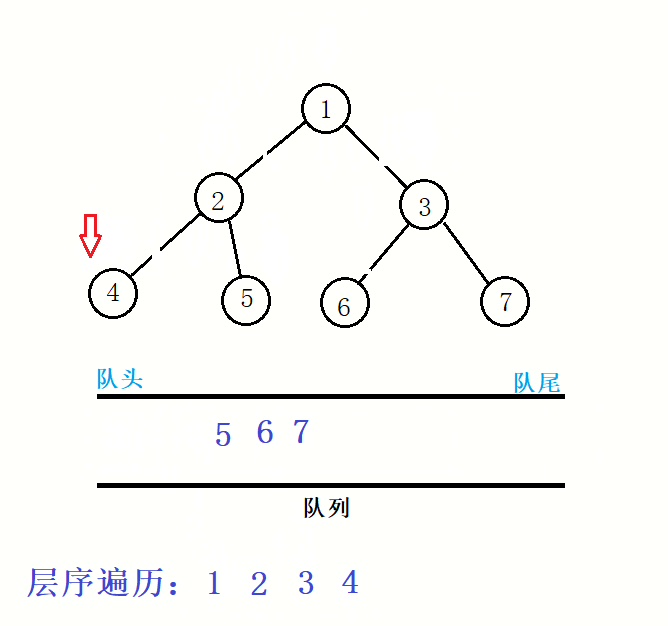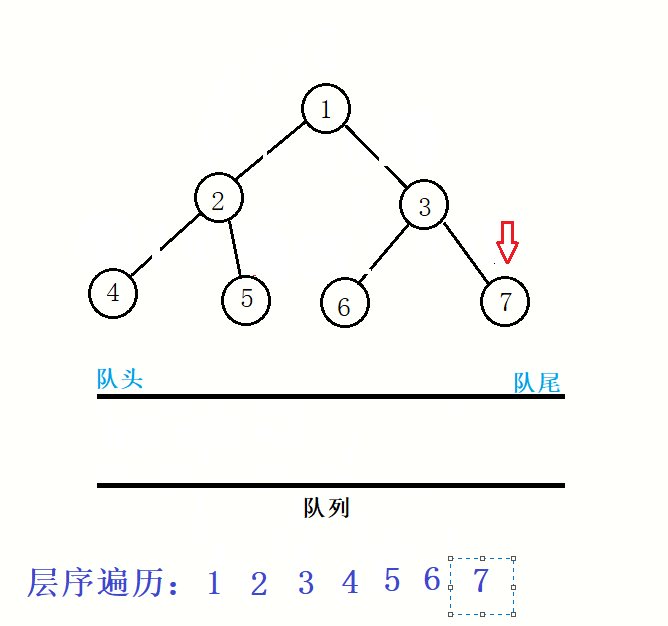
代码:
//层序遍历
void LevelOrder1(BTNode* root)
{Queue Q; //创建队列QueueInit(&Q); //初始化队列QueuePush(&Q, root); //将第一个结点的指针入队//循环出队,直到队空while (!QueueEmpty(&Q)){BTNode* tmp = QueueFront(&Q);//出队头数据QueuePop(&Q);//删除队头数据printf("%d ", tmp->val);//如果出队结点的左孩子不为空就进队if (tmp->left){QueuePush(&Q, tmp->left);}//如果出队结点的右孩子不为空就进队if (tmp->right){QueuePush(&Q, tmp->right);}}QueueDestroy(&Q);
}

三.二叉树节点数
我们利用二叉树的结构特点,利用递归思想来计算二叉树的结点个数,一个二叉树我们看成由根节点,左子树,右子树,那么一颗二叉树的结点个数,就是根节点数,加上左子树结点个数,加上右子树节点个数。
代码:
//节点数
int SizeNode(BTNode* root)
{//如果是空树,没有一个结点,那就返回0if (root == NULL){return 0;}int Lsize = SizeNode(root->left); //左子树结点个数int Rsize = SizeNode(root->right); //右子树结点个数return Lsize + Rsize + 1; //根+左+右
}

四. 叶子结点数
首先我们要知道,叶子结点的特点,叶子节点没有左右孩子,或者左右孩子都是空。这样的结点才能是叶子节点。我们利用递归的思想怎么解释这个问题呢?我们只需要左子树的叶子数加上右子树的叶子数。
代码:
//叶子数
int LeafSize(BTNode* root)
{ //空树没有结点返回0if (root == NULL){return 0;}//如果是叶子,就返回1if (root->left == NULL && root->right == NULL){return 1;}int LLeafsize = LeafSize(root->left); //左子树叶子节点数int RLeafsize = LeafSize(root->right); //右子树叶子节点数return LLeafsize + RLeafsize;
} 
五.最大高度
二叉树的最大深度,利用递归的思想来解释,可以看成左右子树较大的高度加上一个根节点,就是这棵树的做大高度。
代码:
int BTdeep(BTNode*root)
{//空树高度为0if (root == NULL){return 0;}int Ldeep = BTdeep(root->left); //左子树高度int Rdeep = BTdeep(root->right); //右子树高度return (Ldeep > Rdeep? Ldeep : Rdeep) + 1; //左右子树较高的一棵树高度加上一
}六.查找二叉树结点
利用递归的思想,查找二叉树结点并返回出来,找不到返回NULL。我们先判断根节点是不是我们查找的结点,如果根节点不是,再查找左子树和右子树是否有目标结点。如果左右子树都没有,根节点又不是,就返回NULL。
代码:
//查找节点
BTNode* FindNode(BTNode* root, int x)
{//空树没有一个结点if (root == NULL)return NULL;//如果根节点是我们的目标结点,就直接返回if (root->val == x)return root;//查找左子树BTNode* Lfind = FindNode(root->left, x);if (Lfind)//如果左子树找到的不是空,就代表找到了return Lfind;//查找右子树BTNode* Rfind = FindNode(root->right, x);if (Rfind)//如果右子树找到的不是空,就代表找到了return Rfind;return NULL;
}测试:

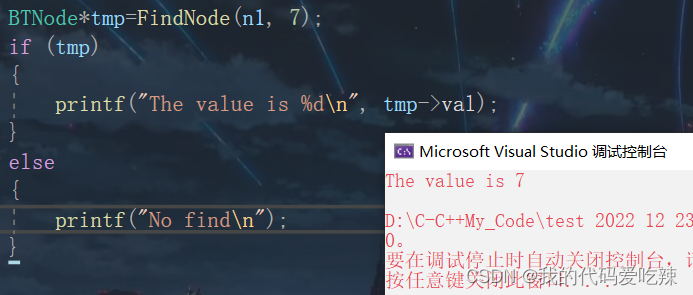
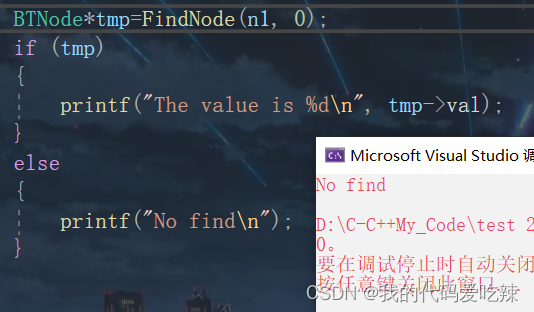
七.二叉树的销毁
销毁一颗二叉树,我们应该借助,后序遍历的思想,最后销毁根节点,不然我们提前销毁根节点了,就会导致无法销毁另一颗子树。
代码:
//二叉树的销毁
void TreeDestory(BTNode* root)
{if (root == NULL){return NULL;}TreeDestory(root->left);TreeDestory(root->right);free(root);
}八.二叉树的创建
牛客——二叉树的创建和遍历

思路:我们利用先序遍历的思路,遍历数组的同时,判断是否是有效的结点,先创建根,在创建左子树,最后创建右子树,最后返回根结点。
#include <stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<string.h>typedef char BTDataType;typedef struct BTNode
{BTDataType val;struct BTNode* Lchild;struct BTNode* Rchild;
}BTNode;
BTNode* BinaryTreeCreate(BTDataType* a,int* pi)
{if(a[*pi]=='#'){(*pi)++;return NULL;}//创建根节点BTNode*root=(BTNode*)malloc(sizeof(BTNode));root->val=a[(*pi)++];//创建左子树root->Lchild=BinaryTreeCreate(a, pi);//创建右子树root->Rchild=BinaryTreeCreate(a, pi);return root;
}void PrevOrder(BTNode* root)
{if (root == NULL){return;}PrevOrder(root->Lchild);printf("%c ", root->val);PrevOrder(root->Rchild);
}
int main() {char arr[101];scanf("%s",arr);int i=0;BTNode*root1=BinaryTreeCreate(arr, &i);PrevOrder(root1);return 0;
}