古希腊有一位大学者，名叫苏格拉底。一天，他带领几个弟子来到一块麦地边。那正是收获的季节。地里满是沉甸甸的麦穗。苏格拉底对弟子们说：你们去麦地里摘一个最大的麦穗，只许进不许退，我在麦地的尽头等你们。

上面是一个经典的寓言故事，这个问题其实有一个数学上的解决办法，这个办法就是最优停止法则。具体的做法就是在走完全程的37%之前一定不要做出选择，但是在走完37%之后，只要见到了比前面37%里面的麦穗都要大的那一棵，就立刻做出决定。这类问题最显著的特点就是严格的连续性，也就是有进无退的单向前进。这个结论也是用数学期望不断算出来的。

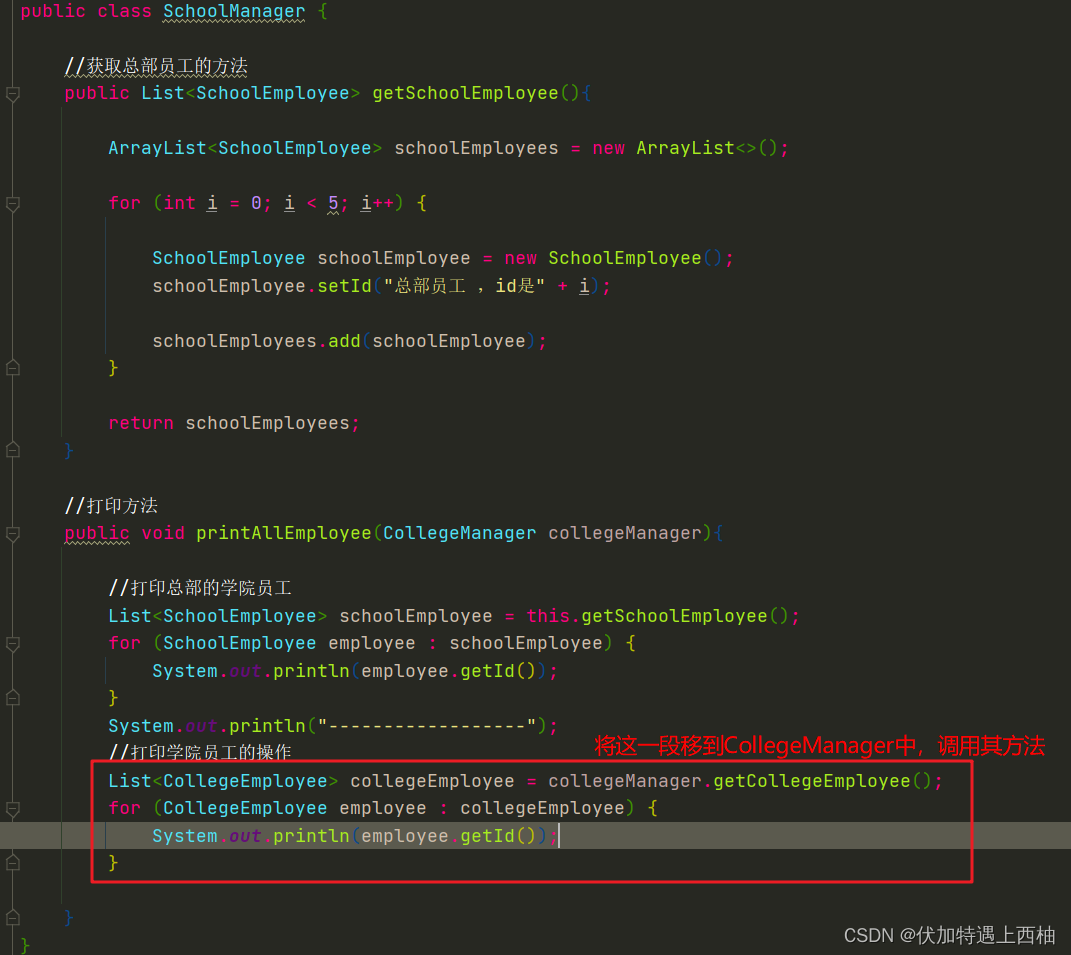
我觉得这个结论还是挺有意思的，于是写了一段代码来模拟一下：

可以看出代码跑出来的结果，和这个结论是非常的相符的。

另外，最优停止理论解决的问题场景也可以分为以下两种：全信息与无信息博弈。无信息博弈不断调整期望值和权衡标准。全信息博弈，就像刚才代码模拟的那样，有一套固定的评价标准。无信息博弈，就好像是找对象或者租房子这种，各种因素所占的比重会有所变化。

数学当然也不能解决生活中的所有问题，时序决策问题可能没有最优停止法则。比如要么三倍，要么赔光的博弈游戏，有一半的概率获得三倍的收入，有一半的概率全部赔光。假如你有一块钱参与这个游戏，第一轮游戏的现金期望值是一块五，如果进入到第二轮游戏，那么第二轮游戏的平均收益就是四块五。数学计算的结果表明应该一直玩下去，但事实上如果真的这么做，最后一定会全部输光。

我们永远没有二次选择的机会。直觉告诉我们合理的选择需要穷举所有选择逐一权衡，然后从中找出效果最好的那个选择，但是实际上随着时间的流逝，决策活动的其他方面都会逐渐淡化，这进一步凸显出停止时机选择的重要性。

具体代码在这里，仓库里还有别的我整理的复习笔记。

https://github.com/Jdroida/free_learning/blob/master/src/BestStopTheory.java