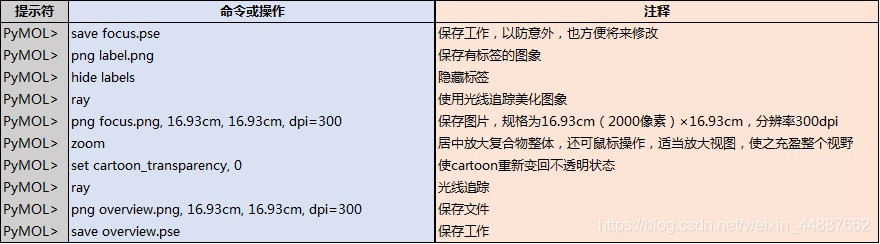
先看题：

 P3067 [USACO12OPEN]Balanced Cow Subsets G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

说实话，洛谷的题解的确是有点难懂，所以本菜在这里写一个比较易懂的思路和代码：

首先先说用什么算法，这里用的是折半搜索，即先搜索0~n/2-1，然后将我们需要的信息记录下来，然后我们在搜索n/2~n-1，用得到的信息与0~n/2-1得到的信息进行比对，然后寻找答案；

【说实话，理解折半搜索的好方法是去写leetcode里的《三数之和》，其根本是空间换时间，但仅仅知道这一点还是不够】

这里我们先抽象一下题目：

我们想象是给每头牛一个权值【英语不好的可以百度翻译喔】，这个权重可以是0，-m，m，【m为一头牛的产奶量】，然后依次给完每个权值后，要求每头牛的权值相加为0，问这种方案有多少种；

抽象完题目后就简单了，我们进行搜索的方法也有了，即每一头牛的状态有3种，给0权，给负权，给正权，这里就对应dfs搜索一个节点的3个分支。

所以dfs中有一个形参确认了，即sum，这里sum记录的是已经给出去的权值相加起来是多少；

当然，还有一个形参c，代表dfs进入多少层了；

那么第一次循环我们要记录什么信息呢？？

说这一点前，我们先考虑怎么连接两次搜索，即怎么用第一次搜索的结果来结合第二次搜索寻找答案；

想搞清楚这个问题，我们找的是什么，这个很容易想到，在前面就说了，我们要找和为0的方案；

那好，我们已经知道了任意给权的情况下，前半部分的权值和，那么如果我们进行第二次搜索，得到一种情况A【这里的A情况只考虑n/2~n-1这些牛的给权情况】，A情况下的权和为sum，那么我们只需要找到前半部分和为-sum的情况个数，然后就可以确认一种情况了；

这里要考虑用什么容器，因为我们要给出一个值，然后快速找到对应的值，这里毫无疑问用unordered_map，即我们用第二次搜索得到的sum来确认第一次搜索的结果；

但是我们还得考虑到一种情况，即题目说的是拿出任意头牛进行给权，但是，拿出来的牛可能有多种给权为0的方式；

比如 1 2 4 2 1   给权可以为  0 2 0 -2 0，也可以为 -1 0 0 0 -1，但是由题意可知，这几头牛是一样的，所以为一种方案，所以我们这边要去重，对于这种多对一的去重，我们可以用id码来去重，即找到上面12421这个放案所有给权后和为0的方案的共同点，然后根据这个共同点来去重；

这个共同点很容易找到，即这些方案选的牛的编号都是相同的，然后我们可以给第一次搜索得到的方案一个编号，即将选哪些牛的状态压缩到一串二进制数里，1为选，0为不选；

然后第二次搜索也给一个id号，这一前一后两个id号就可以结合出一个唯一的id号了，而且这个id号对应的十进制数不大，可以用数组来装下，即st[i]=1表示id号为i的选择方案可行，即按i对应的二进制去选牛的话可以得到一个可行方案；【这里用unordered_map的话会超时】

好，那么讲完了后可以看懂以下代码了【洛谷记得开氧气优化喔】

#include<iostream>
#include<algorithm>
#include<vector>
#include<unordered_map>
using namespace std;const int N=1<<21;int val[N];//记录每一头牛的产奶量
bool ha[N];//ha[i]=1表示id号为i的方案可行，=0时表示不可行
unordered_map<int,vector<int>> fix;//记录和为int的值的id
int n;
int ans;void dfs1(int sum,int id,int c){//sum为当前的和，id为当前状态的编号，c为当前递归层数if(c==n/2){fix[sum].push_back(id);//将这个值push到对应的位置return;}dfs1(sum,id,c+1);//给0权dfs1(sum+val[c],id+(1<<c),c+1);//给正权，并将对应的牛在二进制的位置赋值为1dfs1(sum-val[c],id+(1<<c),c+1);//给负权，并将对应的牛在二进制的位置赋值为1
}void dfs2(int sum,int id,int c){if(c==n){vector<int> mid=fix[-sum];//mid里存储着第一次搜索里和为-sum的id号for(int i=0;i<mid.size();i++){if(!ha[id+mid[i]]&&id+mid[i]) ans++,ha[mid[i]+id]=1;//id号为0时为一头牛都不选，由题意可知是不可行方案，但是其权和为0，所以要特判}return;}dfs2(sum,id,c+1);dfs2(sum+val[c],id+(1<<c),c+1);dfs2(sum-val[c],id+(1<<c),c+1);
}int main(){cin>>n;for(int i=0;i<n;i++) cin>>val[i];dfs1(0,0,0),dfs2(0,0,n/2);cout<<ans;}