2021.05.05青蛙过河

（题目来源：https://leetcode-cn.com/problems/frog-jump/）

题目描述

一只青蛙想要过河。假定河流被等分为若干个单元格，并且在每一个单元格内都有可能放有一块石子（也有可能没有）。青蛙可以跳上石子，但是不可以跳入水中。

给你石子的位置列表 stones（用单元格序号升序表示），请判定青蛙能否成功过河（即能否在最后一步跳至最后一块石子上）。

开始时，青蛙默认已站在第一块石子上，并可以假定它第一步只能跳跃一个单位（即只能从单元格 1 跳至单元格 2 ）。

如果青蛙上一步跳跃了 k 个单位，那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。另请注意，青蛙只能向前方（终点的方向）跳跃。

思路

【TLE】思路1：dfs

通过遍历所有跳石头的情况，直到跳到最后一块石头，返回true。
由于是盲目地跳石头，会出现多次通过k步跳到第i块石头的状态

【TLE】思路2：动态规划

为了防止盲目，记下之前的一些子状态。
定义状态：dp[i][j] :能通过第i块石头跳到第j块石头。跳的步数为arr[j]-arr[i]。
状态转移方程：
若满足：
$k = = (l a s J u m p) = = > i = = (c u r J u m p) = = > j$
且：
$l a s = = c u r ∣ ∣ l a s = = c u r - 1 ∣ ∣ l a s = = c u r + 1$
则：
$d p [i] [j] = d p [i] [j] ∣ ∣ d p [k] [i];$

但是，由于找到前一块石头需要遍历，所以导致TML。

【优化】思路2：动态规划+二分查找

查找前前个石头时，采用二分查找
优化后代码如下：

	public boolean canCross(int[] arr) {int n = arr.length;if(n == 2) return arr[1]-arr[0] == 1;//定义状态：//dp[i][j] == true：第i到第j个是可以到达的，可以计算步数k = arr[j]-arr[i]  (i < j)//k ==(arr[i]-arr[k])==>  i  ==(arr[j]-arr[i])==>  j  boolean[][] dp = new boolean[n][n]; dp[0][0] = true; dp[0][1] = (arr[1]-arr[0] == 1);for(int j = 1; j < n; j++) {for(int i = j-1; i >= 1; i--) {int cur = arr[j]-arr[i];//上一步是 cur / cur-1 / cur+1if(cur-1>i) break; //优化，提前跳出该情况//上一步的所有可能步长for(int las = cur-1; las <= cur+1; las++) {int ind = Arrays.binarySearch(arr, 0, i, arr[i]-las);if(ind >= 0) dp[i][j] = dp[i][j] || dp[ind][i];}if(j == n-1 && dp[i][j]) return true; }}return false;}

思路3：动态规划

为了找到更好的状态转移方程以防止需要循环查找前前个石头，需要改变状态定义。
定义状态 dp[i][k] : 能否通过跳k步跳到第i块石头。（由于步长每次最多递增1步的限制，所以状态矩阵的第二维也不会超过n。
状态转移方程：
(1)状态转移描述
假设从第j块石头跳到第i块石头跳了k步，但是k必须满足“跳到第j块石头是通过跳了k或k-1或k+1步”
(2)将描述通过方程表达

dp[i][k] = dp[j][k] || dp[j][k-1] || dp[j][k+1]

代码如下：

	public boolean canCross(int[] stones) {int n = stones.length;//定义状态：//dp[i][j] == true：到达第i个单元，跳了k步，boolean[][] dp = new boolean[n][n]; dp[0][0] = true;for(int i = 1; i < n; i++) {for(int j = i-1; j >= 0; j--) {//跳的步数int k = stones[i] - stones[j]; //上一次跳的最少步数为k-1，如果最少步数都超过了j，则说明不符合if(k-1 > j) break; dp[i][k] = dp[j][k-1] || dp[j][k] || dp[j][k+1];//可以在循环中判断，也可以在dp矩阵初始化完成后再判断。if(i == n-1 && dp[i][k] == true) return true;}}return false;}

思路4：记忆化搜索+Map

由于Map查找效率高，可以完成以下操作：
(1)存储历史状态，查找当前处理的情况之前有没有已经处理过。
(2)查找一个位置是否有石头，即一个数x是否在stones[]数组中。
进行dfs搜索。

代码：

	//<石头的位置, 数组中下标>Map<Integer, Integer> map ; //用于存放石头的位置，方便之后查找Map<Integer, Boolean> cache; //存储的是之前遍历的结果public boolean canCross(int[] stones) {map = new HashMap<>();cache =new HashMap<>();for (int i = 0; i < stones.length; i++) {map.put(stones[i],i);}//默认 第一位置只能跳1个单位return dfs(stones,0,1);}private boolean dfs(int[] stones,int start,int k){// key的映射函数Integer key = stones[start] * 2000 * 2000 + k;//如果之前已经处理过该状态if(null != cache.get(key)) return cache.get(key);//查找下一个位置是否存在int index = map.getOrDefault(stones[start] + k,-1);//跳不到 || 回头跳 || 原地跳if(index == -1 || index <= start) {cache.put(key, false);return false;}// 跳到最后if(index == stones.length-1) {cache.put(key, true);return true;}// 跳k k-1 k+1 只要任意一个跳到就可以boolean b = dfs(stones, index, k + 1) || dfs(stones, index, k) || dfs(stones, index, k - 1);cache.put(key,b);return b;}

2021.5.19题外话：

再看此种解法，产生了以下问题：

为何需要记录一个key(start, step)的映射？
答：在定义状态时，我们定义决定一个状态共有两个参数，即当前的位置i和跳到i块石头的步数step，所以为了避免重复遍历状态，我们需要建立key(start, step)的映射函数。
即对于状态(i , k)，如果其不能遍历到终点，我们回溯时返回false，其他分支遍历过程中再次遇到此状态，可以直接返回false。
会不会根本不会出现重复的“从j跳k步到i”的状态呢，只会出现“重复遍历到位置i”。
答：错。
若按照上述依据写代码：

在这里插入图片描述

仍报超时错误。故再思考。
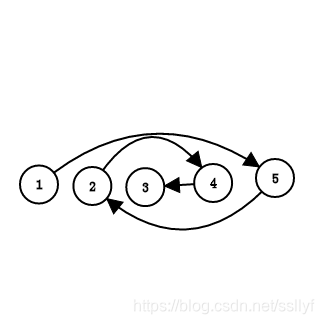
参考别人的图解，以[1,2,3,4,5,999]为例，见图：

在这里插入图片描述](https://img-blog.csdnimg.cn/d999be69fa884b94bc42275fbd22dd4b.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWmFja196Y196Yw==,size_17,color_FFFFFF,t_70,g_se,x_16)

在这里插入图片描述