一问题描述

有一棵摩天大树，在树的每个分支节点上都有一个整数，可否在树上找到这样一个链，以便链上所有整数的乘积（mod 10^6+3）都等于k ？

二输入和输出

1 输入

输入包含几个测试用例。每个测试用例的第 1 行都包含两个整数 N（1≤N ≤10^5 ）和 k（0≤k <10^6 +3）。接下来的一行包含 N 个数字 vi （1≤vi <10^6 +3），其中 vi 表示节点 i 上的整数。然后是 N -1 行，每行都包含两个整数x、y ，表示节点 x 和节点 y 之间的无向边。

2 输出

对每个测试用例，都单行输出两个整数 a 和 b （a <b），表示满足条件的链的两个端点。若存在多个解决方案，则输出字典顺序最小的解决方案。若不存在解决方案，则输出“No solution”。

三输入和输出样例

1 输入样例

5 60

2 5 2 3 3

1 2

1 3

2 4

2 5

5 2

2 5 2 3 3

1 2

1 3

2 4

2 5

2 输出样例

3 4

No solution

四分析

根据测试用例1，构建的树如下图所示。

在上图中存在两条链上节点整数的乘积为 60 的链。

3-1-2-4：2×2×5×3=60。

3-1-2-5：2×2×5×3=60。

输出字典序最小的 3 和 4。

测试用例 2 的输入数据与测试用例 1 相同，但不存在乘积等于 2 的链。

本问题要求在树上找到一个链，链上所有整数的乘积（mod 10^6+3）都等于 k ，可采用点分治算法解决。

若树的重心为 root，则对于一条链 (u , v ) 可分为两种情况：

① 经过 root。

② 不经过 root，如下图所示。

只需求解第 1 种情况，对第 2 种情况继续重心分解即可。

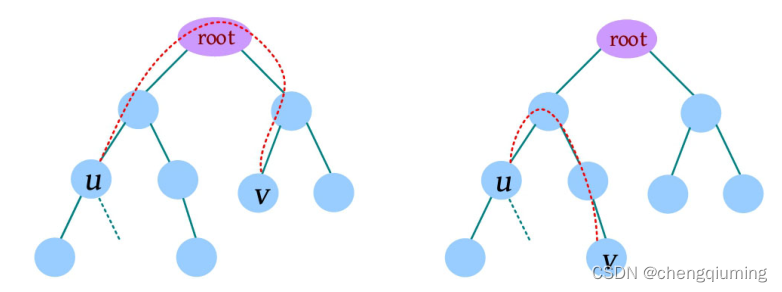
对第 1 种情况的处理方法：遍历子树，将 root 到节点 u 路径上节点的乘积存储到 d[u ]，如果一条链 (u,v) 满足 d[v]×d[u]/val[root]=k，则 u 和 v 配对构成一组解。因为在计算 d[v] 和 d[u]时，root 节点的值被乘了两次，所以再除以 val[root]即可。整理上面的公式可得 d[v]=k×val[root]/d[u]。除以一个数等同于乘以这个数的逆元，如果 inv[d[u]] 为 d[u] 的逆元，则公式变为 d[v ]=k×val[root]×inv[d[u ]]。

本问题求解字典序最小的答案，因此找到了满足条件的解后，更新最小的答案即可。

五算法设计

1 求 1 .. P-1 的逆元，P=10^6 +3。

2 求树的重心 root。

3 从 root 出发，深度优先遍历。val[u]表示节点 u 的值，dev[u] 表示 root 到 u 路径上节点值的乘积，mp[dev[u]] 表示将积映射到编号 u 。积映射的目的是更新字典序更小的答案。

4 对 root 的每棵子树 v ，都求解子树 v 中每个节点到 root 路径上节点的积 x ，查询与该节点配对的另一节点的积 inv[x]×val[root]×k%P ，判断该积是否映射有节点，若没有，则说明该节点不存在，直接返回，否则根据该节点的字典序更新答案，如下图所示。子树 v 中的所有节点在查询完毕后都把积 x 映射到节点 b ，保证不在一棵子树内查询。

5 查询完毕后再把这些积映射清零，然后对每棵子树都进行重心分解并递归求解。

六逆元问题

逆元素指一个可以取消另一给定元素运算的元素，在数学中，逆元素广义化了加法中的加法逆元和乘法中的倒数。乘法逆元指数学领域群 G 中的任意一个元素 a ，在 G 中都有唯一的逆元 a-1 ，有性质 a×a-1 = a-1 ×a = e ，其中 e 为该群的单位元。例如，求 4 关于 1 模 7的乘法逆元：4x ≡ 1 mod 7，等价于求一个 x 和 k ，满足 4x =7k +1，其中 x 和 k 都是整数；当k = 1 时，x =2，4 关于 1模7 的乘法逆元为2。i 关于 1 模 P 的乘法的逆元为 inv[i ] = (-P /i )×inv[P %i ]%P。

七代码

package com.platform.modules.alg.alglib.hdu4812;public class Hdu4812 {public int inf = 0x3f3f3f3f;public int P = 1000003;private int maxn = 100005;long inv[] = new long[P + 5]; // inv存储逆元,int mp[] = new int[P + 5]; // mp将乘积映射到节点long val[] = new long[maxn]; // 节点的值long d[] = new long[maxn]; // 节点到树根的乘积long dep[] = new long[maxn]; // 乘积序列int cnt, n, k, top;int head[];int id[] = new int[maxn]; // id[] 为节点序列int root, S;int size[] = new int[maxn];int f[] = new int[maxn];boolean vis[];int ans1, ans2;edge edge[] = new edge[maxn * 2];public String output = "";public Hdu4812() {for (int i = 0; i < edge.length; i++) {edge[i] = new edge();}}public String cal(String input) {int u, v;get_inv(); // 求1..P-1 的逆元int count = 0;String[] line = input.split("\n");while (true) {if (count == line.length) {break;}String[] num = line[count++].split(" ");n = Integer.parseInt(num[0]);k = Integer.parseInt(num[1]);vis = new boolean[maxn];cnt = 0;ans1 = ans2 = inf;head = new int[maxn];String[] vals = line[count++].split(" ");for (int i = 1; i <= n; i++) {val[i] = Long.parseLong(vals[i - 1]);}for (int i = 1; i < n; i++) {String[] connect = line[count++].split(" ");u = Integer.parseInt(connect[0]);v = Integer.parseInt(connect[1]);add(u, v);add(v, u);}root = 0;S = n;f[0] = n + 1;getroot(1, 0);solve(root);if (ans1 == inf)output += "No solution\n";elseoutput += ans1 + " " + ans2 + "\n";}return output;}void add(int u, int v) {edge[++cnt].to = v;edge[cnt].next = head[u];head[u] = cnt;}// 求 1..P-1 的逆元void get_inv() {inv[1] = 1;for (int i = 2; i < P; i++)inv[i] = ((-P / i) * inv[P % i] % P + P) % P;}// 获取重心void getroot(int u, int fa) {size[u] = 1;f[u] = 0; // 删除 u 后，最大子树的大小for (int i = head[u]; i > 0; i = edge[i].next) {int v = edge[i].to;if (v != fa && !vis[v]) {getroot(v, u);size[u] += size[v];f[u] = Math.max(f[u], size[v]);}}f[u] = Math.max(f[u], S - size[u]); // S为当前子树总结点数if (f[u] < f[root])root = u;}// 获取乘积void getdep(int u, int fa) {dep[++top] = d[u]; // 保存乘积序列id[top] = u; // 保存节点for (int i = head[u]; i > 0; i = edge[i].next) {int v = edge[i].to;if (v != fa && !vis[v]) {d[v] = (d[u] * val[v]) % P; // 乘积 MOD Pgetdep(v, u);}}}void query(long x, int id) { // 积，节点编号x = inv[(int) x] * val[root] * k % P; // 求另一顶点的积int y = mp[(int) x];//映射到编号if (y == 0) return;// 保证 id>yif (y > id) {int temp = y;y = id;id = temp;}// 更新答案为最小编号if (y < ans1 || (y == ans1 && id < ans2)) {ans1 = y;ans2 = id;}}// 获取答案void solve(int u) {vis[u] = true;mp[(int) val[u]] = u; // 值映射到编号for (int i = head[u]; i > 0; i = edge[i].next) {int v = edge[i].to;if (!vis[v]) {top = 0; // 先求以v为根的子树d[v] = val[v] * val[u] % P; // 当前节点值为初值getdep(v, u);for (int j = 1; j <= top; j++) // 查询完毕再把这些积映射，以便下一个子树查询query(dep[j], id[j]); // 第一个子树查询时，只有树根有映射，由此保证不会在一棵子树内部查询，因为这些节点还没有映射for (int j = 1; j <= top; j++)if (mp[(int) dep[j]] == 0 || mp[(int) dep[j]] > id[j]) // 0 或 id[j] 比原来的值映射小mp[(int) dep[j]] = id[j];}}mp[(int) val[u]] = 0; // 刚才赋值的 mp[] 清零for (int i = head[u]; i > 0; i = edge[i].next) {int v = edge[i].to;if (!vis[v]) {top = 0;d[v] = (val[u] * val[v]) % P;getdep(v, u);for (int j = 1; j <= top; j++)mp[(int) dep[j]] = 0;}}for (int i = head[u]; i > 0; i = edge[i].next) {int v = edge[i].to;if (!vis[v]) {root = 0;S = size[v];getroot(v, 0);solve(root);}}}
}class edge {int to, next;
}