系列文章目录

---

---

前言

c++基础算法。

---

一、排序

（1）快速排序

核心思想

基于分治的思想：

1. 确定分界点x：取左边界q[l]，或者取中间值q[(l+r)/2]，或者取右边界q[r]，也可以随机。
2. 调整区间(较难部分)：让小于等于x的数在一个区间，大于x的在另一个区间
3. 递归处理左右两端

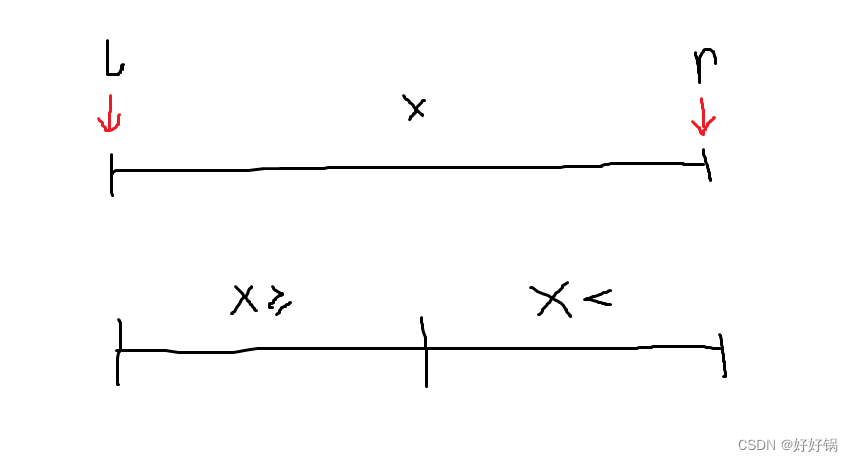
思路分析

思路一：暴力解法，需要额外空间放a b

思路二：较优美的解法
使用双指针，从数组两端向中间靠拢。指针 i 从左端找大于等于 x 的数，指针 j 从右端找小于等于 x 的数，然后swap二者，直至 i 和 j 相遇。

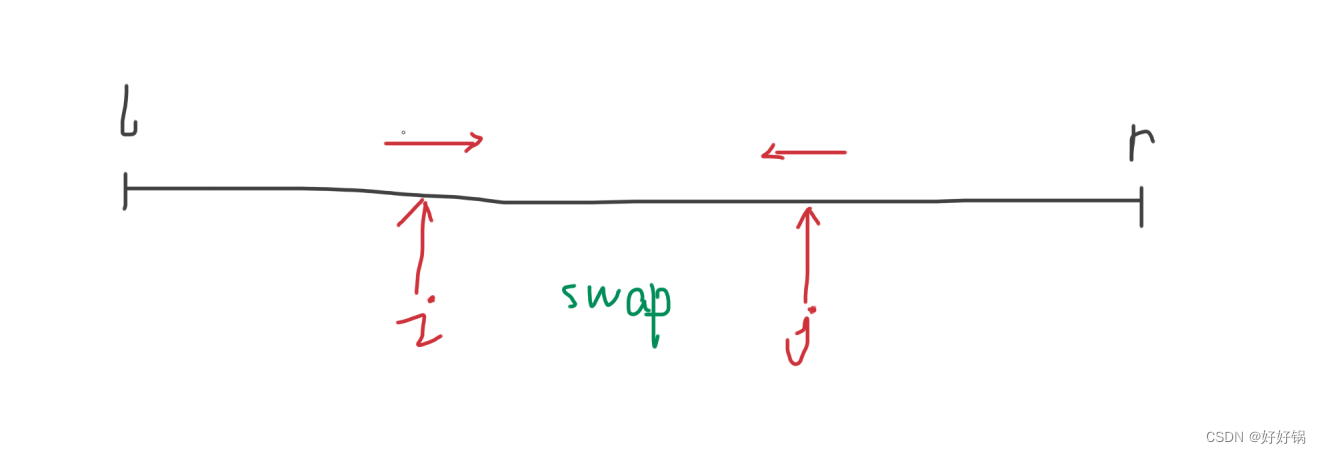
模板

void quick_sort(int q[], int l, int r)
{if (l >= r) return;int i = l - 1, j = r + 1, x = q[l + r >> 1];while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

（2）归并排序

核心思想

也是基于分治的思想：

(1) 确定分界点：mid = ( l + r ) / 2
(2) 递归排序 :left 和 right
(3) 归并(较难部分) ：合二为一

思路分析

思路一：双指针left和right:

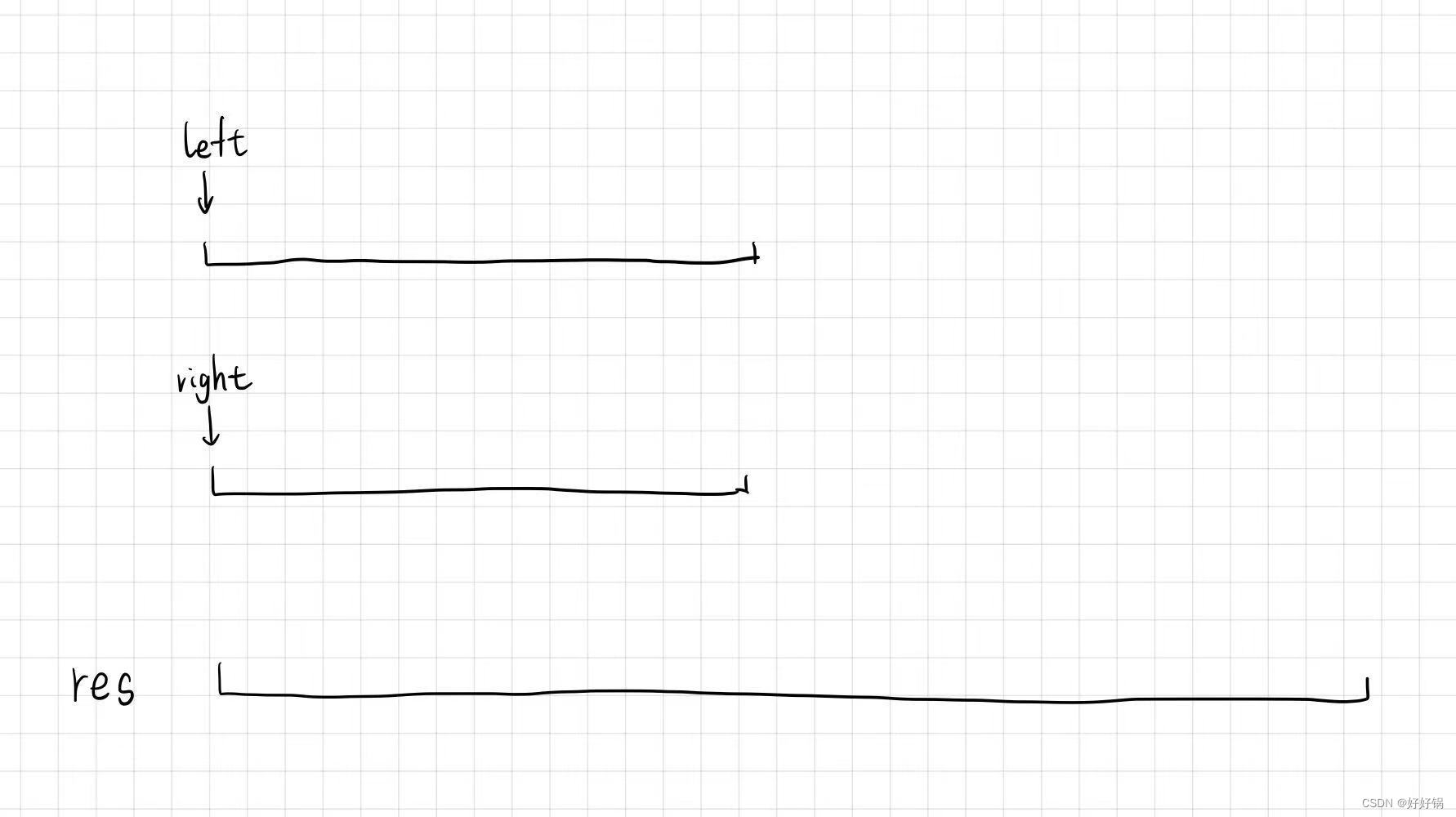
left和right指向的数组是有序的，left 和 right 一一比较，将较小的数放进归并数组 res 中，当一个数组走到头后，将另一个数组的剩下部分直接贴到 res 的后面。

模板

void merge_sort(int q[], int l, int r)
{if (l >= r) return;int mid = l + r >> 1;merge_sort(q, l, mid);merge_sort(q, mid + 1, r);int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else tmp[k ++ ] = q[j ++ ];while (i <= mid) tmp[k ++ ] = q[i ++ ];while (j <= r) tmp[k ++ ] = q[j ++ ];for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

稳定性

排序算法的稳定性是指：对于原数组中相同的数，若排序后这些相同数的相对位置不发生改变，则该算法是稳定的。
快排是不稳定的，归并是稳定的。

时间复杂度

平均时间复杂度： O(nlogn)
快速排序：每层期望是 n/2 ，递归深度 logn，故平均时间复杂度 O(nlogn)。
归并排序：每层期望是n，递归深度logn，故平均时间复杂度 O(nlogn)。

二分查找

（1）整数二分

核心思想

有单调性一定可以二分，但是可以二分的题目不一定非要有单调性。
找到一个边界将区间划分为两部分，使得一部分满足，另一部分不满足。

思路分析

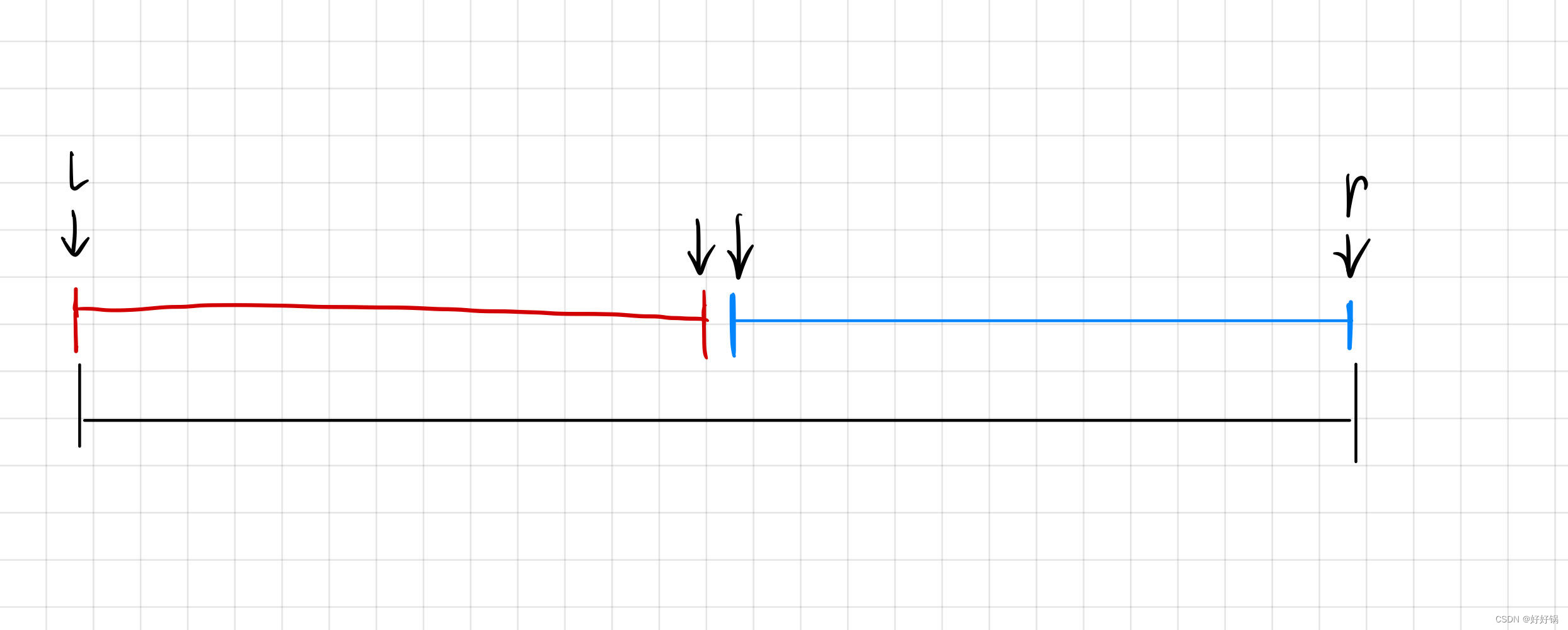
第一种情况：红色边界点
check (mid) 判断 mid 是否满足红颜色的性质。注意 mid = ( l + r + 1) / 2 以及更新区间时的 mid 和 mid-1。

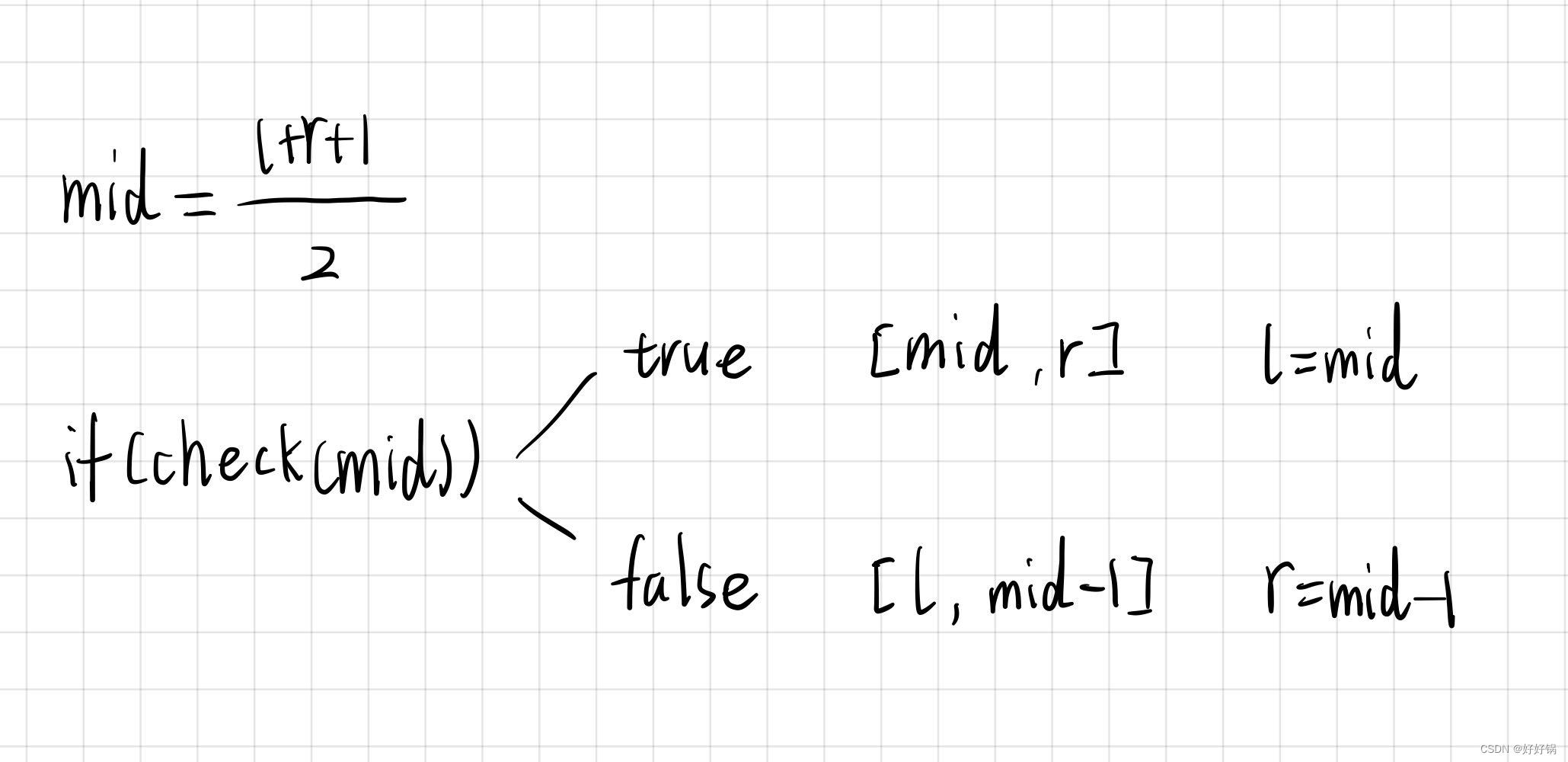
第二种情况：绿色边界点
check (mid) 判断 mid 是否满足绿颜色的性质。注意更新区间时的 mid 和 mid+1。

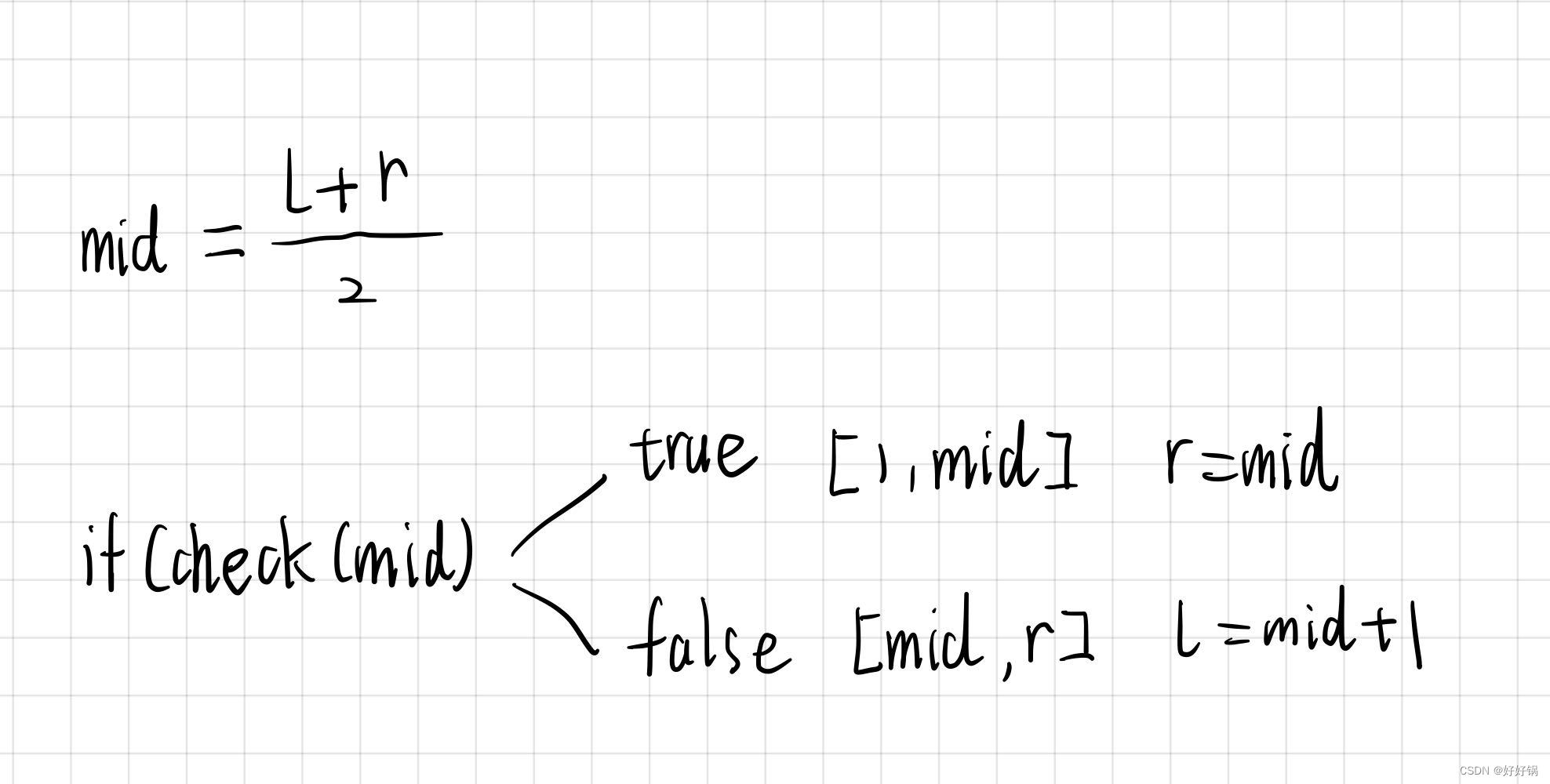
模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;    // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}

（2）浮点数二分

核心思想

double 可以直接除而不会取整，所以不用在意边界问题，较为简单。
判断条件一般为 r - l >= 1e-6.
次数一般取 保留小数点位数+2，例如保留5位小数，就是1e-7.
也可以不用判断，直接 for 循环100次，相当于除以 2 的100次方，得到的位数足够。

模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}

二、

---

总结